CV实验之GoogLeNet网络训练总结
一、GoogLeNet网络结构
GoogleNet模型的网络深度为22层( 如果只计算有参数层,GoogleNet网络有22层深 ,算上池化层则共有27层),而且在网络架构中引入了Inception单元,从而进一步提升模型整体的性能。虽然深度达到了22层,但大小却比AlexNet和VGG小很多,GoogleNet参数为500万个( 5M ),VGG16参数是138M,是GoogleNet的27倍多,而VGG16参数量则是AlexNet的两倍多。
二、GoogleNet 创新点:
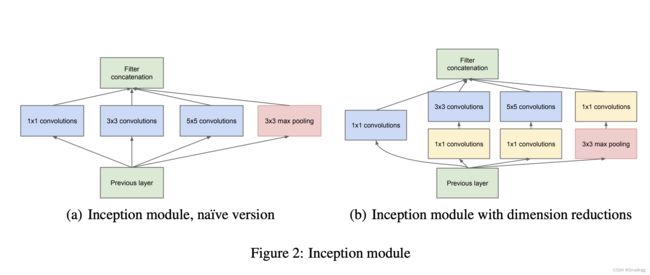
1、Inception结构:利用不同大小的卷积核实现不同尺度的感知,最后进行融合,可以得到图像更好的表征。
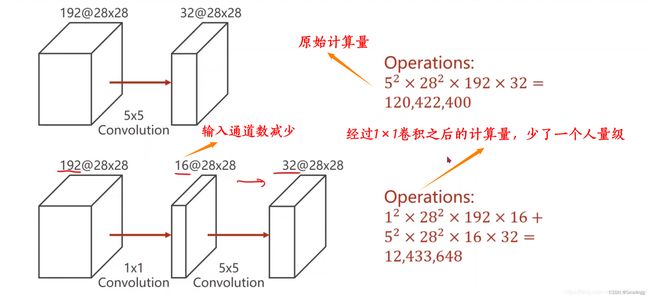
2、使用了1*1卷积:GoogLeNet 在网络中使用了 1x1 的卷积核来进行降维操作,从而减少通道数。这样做既可以减少计算复杂性,又可以提高模型的表达能力。
3、全局平均池化: 在网络的最后,GoogLeNet 使用了全局平均池化操作,将最后一个卷积层的特征图的每个通道的空间维度进行平均,得到一个固定大小的特征向量。这种操作可以降低模型中的参数数量,减少过拟合的风险。
三、训练与测试
我们对原始的GoogLeNet网络做了一些改进:
1、使用了批标准化(Batch Normalization):每个卷积层后面都添加了nn.BatchNorm2d层,这有助于加速网络的训练和提高模型的泛化能力。
2、增加了激活函数:在每个卷积层后面都使用了nn.ReLU(True)。
3、5x5卷积分支的改进:在原始的GoogLeNet中,5x5卷积分支只使用了一个5x5的卷积核。改进后的Inception模块5x5卷积分支使用了两个连续的3x3卷积核来替代,这有助于减少参数量并增加非线性能力。
学习率初始值为0.01,使用的是余弦退火学习率调节器,优化器使用的是SGD随机梯度下降优化器。
原始GoogLeNet模型具体结构:
微调GoogLeNet模型1具体结构:
微调GoogLeNet模型2具体结构:
具体代码如下所示:
main.py
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from torch.nn import init
from torch.optim import Adam
from torch.optim.lr_scheduler import StepLR
from torch.utils.tensorboard import SummaryWriter
from models import *
transform_train = transforms.Compose(
[
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
transform_test = transforms.Compose(
[
transforms.ToTensor(),
transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225))]
)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
trainset = torchvision.datasets.CIFAR10(root='D:\CV\pytorch\dataset\cifar-10-batches-py',
train=True, download=True, transform=transform_train)
trainLoader = torch.utils.data.DataLoader(trainset, batch_size=32, shuffle=True)
testset = torchvision.datasets.CIFAR10(root='D:\CV\pytorch\dataset\cifar-10-batches-py',
train=False, download=True, transform=transform_test)
testLoader = torch.utils.data.DataLoader(testset, batch_size=32, shuffle=False)
writer = SummaryWriter('D:\CV\pytorch\pytorch-cifar-master\logs_googlenet_100ep')
# net = VGG('VGG16')
# net = ResNet50()
net = GoogLeNet()
# net = ResNet18()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9, weight_decay=5e-4) # 0.1,0.01
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=200)
total_times = 100
total = 0
accuracy_rate = []
for epoch in range(total_times):
net .train()
net .to(device)
running_loss = 0.0
total_train_correct = 0
total_train_samples = 0
total_correct = 0
total_trainset = 0
for i, (data, labels) in enumerate(trainLoader, 0):
data = data.to(device)
outputs = net(data).to(device)
labels = labels.to(device)
loss = criterion(outputs, labels).to(device)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
_, pred = outputs.max(1)
correct = (pred == labels).sum().item()
total_correct += correct
total_trainset += data.shape[0]
running_loss += loss.item()
total_train_correct += correct
total_train_samples += data.shape[0]
train_loss = running_loss / len(trainLoader)
train_accuracy = total_train_correct / total_train_samples
writer.add_scalar('Train/Loss', train_loss, epoch)
writer.add_scalar('Train/Accuracy', train_accuracy, epoch)
print('epoch[%d] train_loss: %.4f, train_acc: %.4f' % (epoch + 1, running_loss / len(trainLoader), train_accuracy))
net.eval()
correct = 0 # 预测正确的图片数
total = 0 # 总共的图片数
losses = [] # 用于记录每个批次的损失值
with torch.no_grad():
for data in testLoader:
images, labels = data
images = images.to(device)
outputs = net(images).to(device)
outputs = outputs.cpu()
outputarr = outputs.numpy() # 将output转换为numpy
_, predicted = torch.max(outputs, 1) # 获取每个样本在输出中的最大值以及对应索引,predicted 保存预测类别标签。
total += labels.size(0) # 这是为了计算整个测试集的准确率时,获得正确的总样本数
correct += (predicted == labels).sum() # (predicted == labels) 会生成一个布尔张量.sum() 对布尔张量进行求和,得到预测正确的样本数量。
# 计算测试损失
loss = criterion(outputs, labels)
losses.append(loss.item())
accuracy = 100 * correct / total
accuracy_rate.append(accuracy)
mean_loss = sum(losses) / len(losses) # 平均损失值
writer.add_scalar('Test/Loss', mean_loss, epoch)
writer.add_scalar('Test/Accuracy', accuracy, epoch)
print(f'epoch[{epoch + 1}] test_lost: {mean_loss:.4f} test_acc: {accuracy:.2f}%')
# print(f'测试准确率:{accuracy}%'.format(accuracy))
# test()
scheduler.step()
writer.close()
torch.save(net.state_dict(), 'D:\CV\pytorch\pytorch-cifar-master/res/GoogleNet_100epoch.pth')
accuracy_rate = np.array(accuracy_rate)
times = np.linspace(1, total_times, total_times)
plt.xlabel('times')
plt.ylabel('accuracy rate')
plt.plot(times, accuracy_rate)
plt.show()
print(accuracy_rate)model.py
'''GoogLeNet with PyTorch.'''
import torch
import torch.nn as nn
import torch.nn.functional as F
class Inception(nn.Module):
def __init__(self, in_planes, n1x1, n3x3red, n3x3, n5x5red, n5x5, pool_planes):
super(Inception, self).__init__()
# 1x1 conv branch
self.b1 = nn.Sequential(
nn.Conv2d(in_planes, n1x1, kernel_size=1),
nn.BatchNorm2d(n1x1),
nn.ReLU(True),
)
# 1x1 conv -> 3x3 conv branch
self.b2 = nn.Sequential(
nn.Conv2d(in_planes, n3x3red, kernel_size=1),
nn.BatchNorm2d(n3x3red),
nn.ReLU(True),
nn.Conv2d(n3x3red, n3x3, kernel_size=3, padding=1),
nn.BatchNorm2d(n3x3),
nn.ReLU(True),
)
# 1x1 conv -> 5x5 conv branch
self.b3 = nn.Sequential(
nn.Conv2d(in_planes, n5x5red, kernel_size=1),
nn.BatchNorm2d(n5x5red),
nn.ReLU(True),
nn.Conv2d(n5x5red, n5x5, kernel_size=3, padding=1),
nn.BatchNorm2d(n5x5),
nn.ReLU(True),
nn.Conv2d(n5x5, n5x5, kernel_size=3, padding=1),
nn.BatchNorm2d(n5x5),
nn.ReLU(True),
)
# 3x3 pool -> 1x1 conv branch
self.b4 = nn.Sequential(
nn.MaxPool2d(3, stride=1, padding=1),
nn.Conv2d(in_planes, pool_planes, kernel_size=1),
nn.BatchNorm2d(pool_planes),
nn.ReLU(True),
)
def forward(self, x):
y1 = self.b1(x)
y2 = self.b2(x)
y3 = self.b3(x)
y4 = self.b4(x)
return torch.cat([y1,y2,y3,y4], 1)
class GoogLeNet(nn.Module):
def __init__(self):
super(GoogLeNet, self).__init__()
self.pre_layers = nn.Sequential(
nn.Conv2d(3, 192, kernel_size=3, padding=1),
nn.BatchNorm2d(192),
nn.ReLU(True),
)
self.a3 = Inception(192, 64, 96, 128, 16, 32, 32)
self.b3 = Inception(256, 128, 128, 192, 32, 96, 64)
self.maxpool = nn.MaxPool2d(3, stride=2, padding=1)
self.a4 = Inception(480, 192, 96, 208, 16, 48, 64)
self.b4 = Inception(512, 160, 112, 224, 24, 64, 64)
self.c4 = Inception(512, 128, 128, 256, 24, 64, 64)
self.d4 = Inception(512, 112, 144, 288, 32, 64, 64)
self.e4 = Inception(528, 256, 160, 320, 32, 128, 128)
self.a5 = Inception(832, 256, 160, 320, 32, 128, 128)
self.b5 = Inception(832, 384, 192, 384, 48, 128, 128)
self.avgpool = nn.AvgPool2d(8, stride=1)
self.linear = nn.Linear(1024, 10)
def forward(self, x):
out = self.pre_layers(x)
out = self.a3(out)
out = self.b3(out)
out = self.maxpool(out)
out = self.a4(out)
out = self.b4(out)
out = self.c4(out)
out = self.d4(out)
out = self.e4(out)
out = self.maxpool(out)
out = self.a5(out)
out = self.b5(out)
out = self.avgpool(out)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
def test():
net = GoogLeNet()
x = torch.randn(1, 3, 32, 32)
y = net(x)
print(y.size())
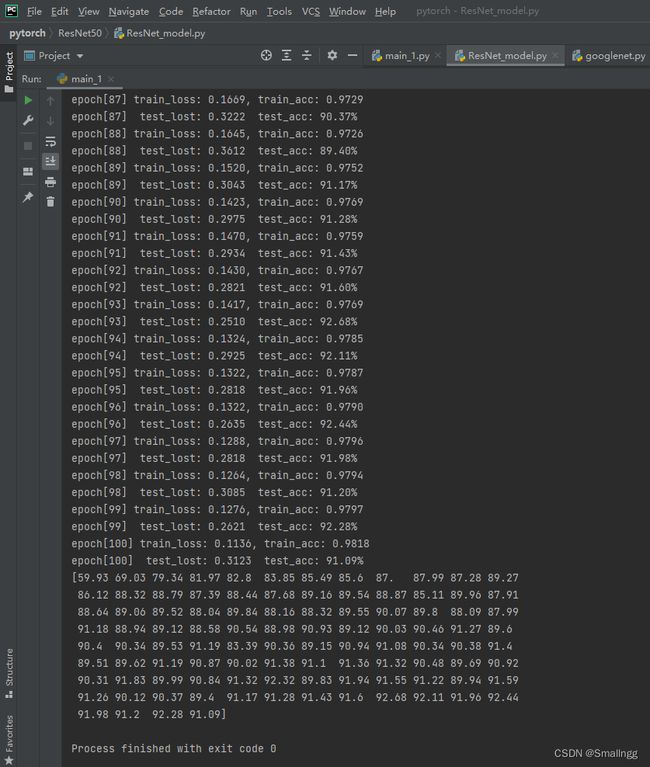
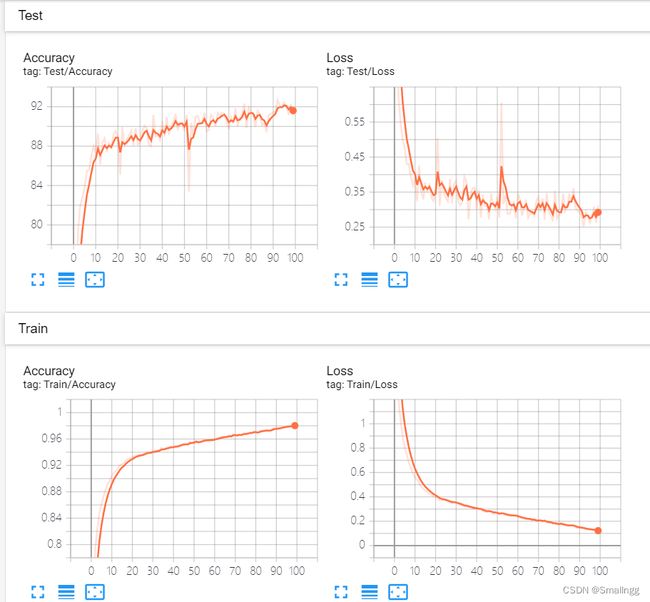
训练和测试的一些参数可以根据自己电脑的算力进行微调。在训练了100个epoch后,在CIRAR10数据集上的最高准确率为92.68%。
参考文献:
深入解读GoogLeNet网络结构(附代码实现)_雷恩Layne的博客-CSDN博客