2023“钉耙编程”中国大学生算法设计超级联赛(3)
Chaos Begin 贪心/凸包
Out of Control DP,递推
Operation Hope 贪心/2-sat与二分
8-bit Zoom 二维前缀
Noblesse Code 轨迹哈希,字典序,差分
2n个点,分为两组,使得第一组整体偏移相同方向和距离能够得到第二组。
考虑,对x降序排序,x相同则y降序排序。然后固定第一个点为第一个集合。暴力枚举与之配对的第二集合的一点,获得dx,dy。然后贪心的去匹配。如果当前点没有被用到,因为dx一定大于等于0,故当前点只能是第一集合点,再以此为标准移动,dx,dy看是否有与之配对点。如果没有,则退出。
而至于题解的“凸包”写法,过于小题大做。
#include
using namespace std;
typedef long long int ll;
paira[500000+10];
map,int>mp,cnt;
int main()
{
cin>>t;
while(t--)
{
int n;
scanf("%d",&n);
mp.clear();
cnt.clear();
for(int i=1; i<=2*n; i++)
{
int x,y;
scanf("%d%d",&x,&y);
a[i].first=x;
a[i].second=y;
cnt[a[i]]++;
}
sort(a+1,a+1+2*n);
set>ans;
for(int i=2; i<=2*n; i++)
{
int dx=a[i].first-a[1].first;
int dy=a[i].second-a[1].second;
mp.clear();
int temp=0;
for(int j=1; j<=2*n; j++)
{
if(mp[a[j]]==cnt[a[j]])
continue;
mp[a[j]]++;
if(mp[make_pair(a[j].first+dx,a[j].second+dy)] dp[i][j]代表i长度时,以j结尾的方案数。而转移方程的获得,观察样例解释最方便获得。即dp[i][j]由全部的dp[i-1][k] 1<=k<=j获得。 其中特别注意的是j的下限,它等于前i个数字由高到低放置的时候的结尾数字。其实也就是sort之后的ai。这里的ai,是我们事先离散化好的。
#include
using namespace std;
typedef long long ll;
ll dp[3030][3030];
# define mod 1000000007
int a[3030],lisan[3030],len;
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
len=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
len++;
lisan[len]=a[i];
}
sort(a+1,a+1+n);
sort(lisan+1,lisan+1+len);
len=unique(lisan+1,lisan+1+len)-lisan-1;
for(int i=0;i<=n;i++)
{
for(int j=0;j<=len;j++)
{
dp[i][j]=0;
}
}
for(int i=1;i<=len;i++)
{
dp[1][i]=1;
}
ll ans=0;
for(int i=2;i<=n+1;i++)
{
for(int j=1;j<=len;j++)
{
dp[i-1][j]+=dp[i-1][j-1];
dp[i-1][j]%=mod;
}
int l=lower_bound(lisan+1,lisan+1+len,a[i])-lisan;
for(int j=l;j<=len;j++)
{
dp[i][j]+=dp[i-1][j];
dp[i][j]%=mod;
}
cout<
题解所说的2-sat+二分+排序+贪心+ Kosaraju解法,过于复杂冷门,且没有充分利用题目条件,即替代方案的a,b,c都大于原始方案的a,b,c。利用这一性质,考虑贪心做法,每次我们获取当前a,b,c最大极差,将造成这一最大极差两个数,小的那个,替换为“替代方案”,也就缩小的极差。这一过程用set维护只需要几十行,复杂度低,常数小,优于题解上百行的2-sat。
而对于题解的2-sat。即二分最终答案,Kosaraju边跑边建图。正向DFS时,当前点只走向冲突点的反点,反向遍历时,获取当前反点的冲突点。而后检查点和反点是否在同一强联通。对于tarjan为什么不能这样写,尚未理解。赛时也没有tarjan过掉的。
#include
using namespace std;
set>s[4];
int book[100000+10];
int a[200000+10][4];
int main()
{
cin.tie(0);
ios::sync_with_stdio(0);
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
book[i]=0;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=3;j++)
{
cin>>a[i][j];
}
for(int j=1;j<=3;j++)
{
cin>>a[i+n][j];
}
}
for(int i=1;i<=3;i++)
s[i].clear();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=3;j++)
{
s[j].insert({a[i][j],i});
}
}
int ans=2e9+10;
while(1)
{
int temp[4];
int maxx=0;
for(int i=1;i<=3;i++)
{
temp[i]=(s[i].rbegin()->first-s[i].begin()->first);
maxx=max(maxx,temp[i]);
}
int flag=0;
ans=min(ans,maxx);
for(int i=1;i<=3;i++)
{
if(temp[i]==maxx)
{
auto [val,id]= *s[i].begin();
if(id<=n)
{
if(book[id]==0)
{
book[id]=1;
for(int j=1;j<=3;j++)
{
s[j].erase({a[id][j],id});
s[j].insert({a[id+n][j],id+n});
flag=1;
}
break;
}
}
}
}
if(flag==0)
break;
}
cout< 模拟即可,注意原图有“颜色块”可以不呈整数倍扩增时,也是可以的。二维前缀和暴力搞就是
#include
using namespace std;
typedef long long ll;
char ans[500][500], a[500][500];
int sum[500][500][30];
int getsum(int x,int y,int xx,int yy,int ch)
{
return sum[xx][yy][ch]-sum[xx][y-1][ch]-sum[x-1][yy][ch]+sum[x-1][y-1][ch];
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n, z;
scanf("%d%d", &n, &z);
int flag = 0 ;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
for(int k=1; k<=26; k++)
{
sum[i][j][k]=0;
}
}
}
char ch = '1';
for (int i = 1; i <= n; i++)
{
for (int j = 1; j<=n; j++)
{
cin >> a[i][j];
if(ch=='1')
{
ch = a[i][j];
}
else if(a[i][j]!=ch)
{
flag = 1;
}
int now=(int)(a[i][j]-'a'+1);
for(int k=1; k<=26; k++)
{
sum[i][j][k]=sum[i][j-1][k]+sum[i-1][j][k]-sum[i-1][j-1][k]+(now==k);
}
}
}
int temp = n * z;
if(temp%100)
{
cout<<"error"<
Problem - 7311
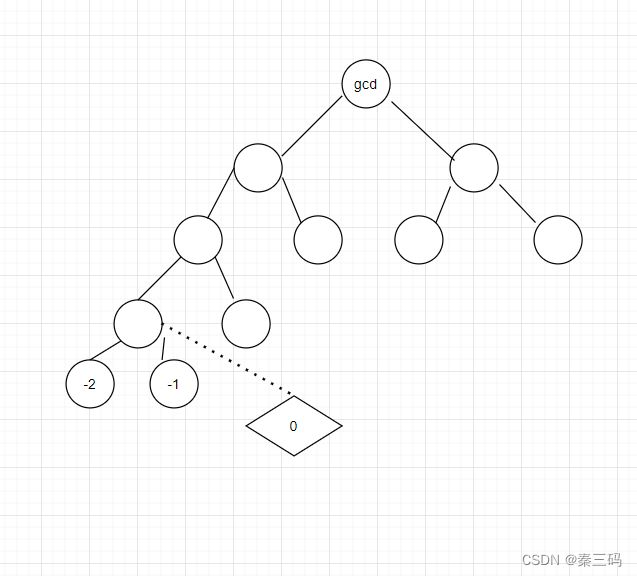
首先这一变换具有一个性质,即除了原始的a,b的大小关系不定外,处于“变化”过程中的a,b是有确定的大小关系的,且可以根据这一大小关系直接推出上一步的变换。我们可以将已知的a,b统一向前倒推,这一方法便是辗转相减,最终会得出gcd。不难发现,这一轨迹的形态,是一颗树。同时,我们对询问的a,b也这样转换。画图易知,一个A,B能够转化为,a,b当且仅当A,B轨迹是a,b轨迹的前缀。
而进一步将前缀关系转化为字典序关系。我们将向左拐为-1,右拐为-2,虚点为0.A,B轨迹确定时,AB为前缀的全部轨迹在,大于等于AB字典序,小于AB+虚点0字典序的范围内。
故可以对已知和询问统一放在一个集合排序,排序规则自定义模拟。字典序相同时,已知的放在后面,询问的放在在前。
这样排序,遇到AB+0时计算当前已知的个数,遇到AB是计算已知个数,二者相减,即可得出答案,也就是大于等于AB,小于AB+0的,减去严格小于AB的。差分的思想,线性解决。
#include
using namespace std;
typedef long long int ll;
inline ll read()
{
ll x = 0, f = 1ll;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 1ll) + (x << 3ll) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
inline void write(ll x)
{
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
struct node
{
int ti;
vectorv;
};
struct node s[500000*3+10];
inline vectorwork(ll x,ll y)
{
vectorans;
while(x!=y)
{
if(x>y)
{
ll pre=x;
x%=y;
if(x==0)
x=y;
ans.push_back((pre-x)/y);
ans.push_back(-1);//左转
}
else
{
ll pre=y;
y%=x;
if(y==0)
y=x;
ans.push_back((pre-y)/x);
ans.push_back(-2);
}
}
ans.push_back(x);
reverse(ans.begin(),ans.end());
return ans;
}
inline int check(const vector&a,const vector&b)
{
int n=a.size(),m=b.size(),i;
if(a[0]!=b[0])return a[0]=n)return -1;
return a[i+2]b[i+1])
{
if(i+2>=m)return 1;
return a[i]>t;
while(t--)
{
int n,m;
n=read();
m=read();
int len=0;
for(int i=1; i<=n; i++)
{
ll a,b;
a=read();
b=read();
len++;
s[len].ti=0;
s[len].v=work(a,b);
}
for(int i=1; i<=m; i++)
{
ll a,b;
ans[i]=0;
a=read();
b=read();
len++;
s[len].ti=-i;
s[len].v=work(a,b);
len++;
s[len].ti=i;
s[len].v=s[len-1].v;
s[len].v.push_back(0);
s[len].v.push_back(0);
}
sort(s+1,s+1+len,cmp);
int nowcnt=0;
for(int i=1; i<=len; i++)
{
if(s[i].ti==0)
{
nowcnt++;
continue;
}
if(s[i].ti<0)
ans[-s[i].ti]-=nowcnt;
else
ans[s[i].ti]+=nowcnt;
}
for(int i=1; i<=m; i++)
{
cout<