第三章 图论 No.8最近公共祖先lca, tarjan与次小生成树
文章目录
-
- lca
- Tarjan
-
- 板子题:1172. 祖孙询问
- lca或tarjan:1171. 距离
- 356. 次小生成树
- 352. 闇の連鎖

lca
O ( m l o g n ) O(mlogn) O(mlogn),n为节点数量,m为询问次数,lca是一种在线处理询问的算法
自己也是自己的祖先
倍增:
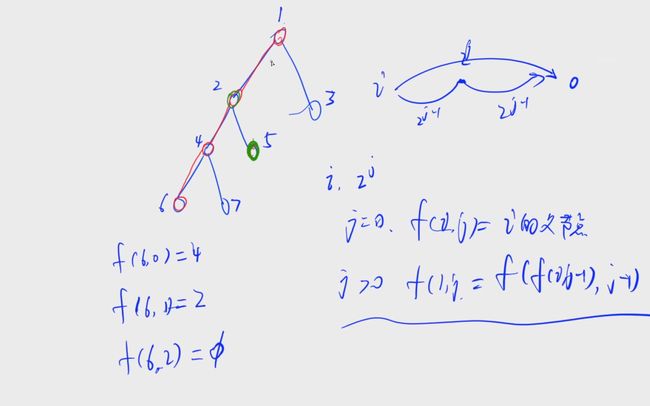
f a ( i , j ) fa(i, j) fa(i,j)表示从i开始,向上走 2 j 2^j 2j步走到的点
j = 0,走到父节点
j > 0,分两步走,先走到 2 j − 1 2^{j-1} 2j−1步再走 2 j − 1 2^{j-1} 2j−1步,那么一共就会走 2 j 2^j 2j步, f a ( i , j ) = f a ( f a ( i , j − 1 ) , j − 1 ) fa(i, j) = fa(fa(i, j-1), j-1) fa(i,j)=fa(fa(i,j−1),j−1)
d e p t h ( i ) depth(i) depth(i)表示层数
- 将两点跳到同一层
- 让两个点同时往上跳,直到跳到公共祖先的下一层
第一步:基于二进制的思想,x和y之间的层数差距为 d e p t h ( x ) − d e p t h ( y ) depth(x) - depth(y) depth(x)−depth(y),假设y的层数小于x的层数,此时x要往上跳
若要跳k层,那么根据k的二进制表示将k拆分成多个2的幂相加,由于我们已经预处理了 f ( i , j ) f(i, j) f(i,j),所以根据 f ( i , j ) f(i, j) f(i,j)的值往上跳即可
当 f ( x , k ) = f ( y , k ) f(x, k) = f(y, k) f(x,k)=f(y,k)时,即x往上跳k步和y往上跳k步后,位于同一个位置,此时找到了一个公共祖先,但不是最近公共祖先,所以这里要减小k的值,直到 f ( x , k ) ≠ f ( y , k ) f(x, k) ≠ f(y, k) f(x,k)=f(y,k),此时才找到了最近公共祖先
规定 d e p t h ( 0 ) = 0 depth(0) = 0 depth(0)=0,0号点为哨兵,位于第0层,根节点位于第一层
向上跳 2 k 2^k 2k步后,若跳出了这颗树,那么 f ( i , k ) = 0 f(i, k) = 0 f(i,k)=0
预处理depth和fa的板子:
void bfs(int root)
{
memset(dis, 0x3f, sizeof(dis));
q[tt ++ ] = root;
depth[root] = 1, depth[0] = 0;
while (tt >= hh)
{
int x = q[hh ++ ];
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (depth[y] > depth[x] + 1)
{
depth[y] = depth[x] + 1;
q[tt ++ ] = y;
fa[y][0] = x;
for (int k = 1; k <= c; ++ k )
fa[y][k] = fa[fa[y][k - 1]][k - 1];
}
}
}
}
lca板子:
int lca(int x, int y)
{
if (depth[x] < depth[y]) swap(x, y);
for (int k = c; k >= 0; -- k )
if (depth[fa[x][k]] >= depth[y])
x = fa[x][k];
if (x == y) return y;
for (int k = c; k >= 0; -- k )
if (fa[x][k] != fa[y][k])
{
x = fa[x][k];
y = fa[x][k];
}
return fa[x][0];
}
Tarjan
O ( n + m ) O(n + m) O(n+m) ,n为节点数量,m为询问次数
tarjan是一种离线处理询问的算法,是向上标记法的优化
在深度优先遍历时,将所有点分成三大类
- 已经遍历过且已经回溯的点
- 已经遍历但正在搜索的分支
- 还未搜索到的点
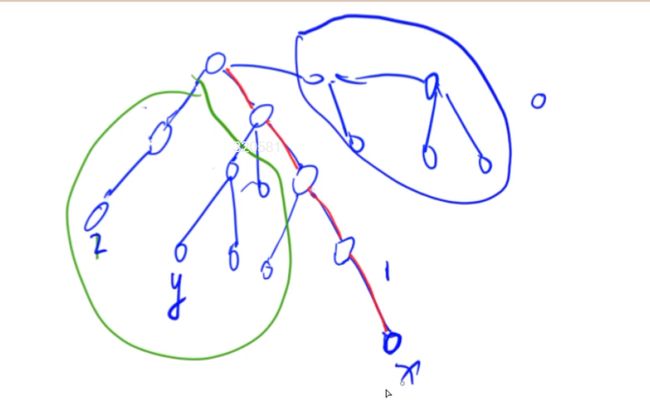
将已经遍历且回溯的点标记成2,正在遍历的点标记成1,未遍历的点标记成0
对于正在回溯的点,需要处理所有有关该点的询问信息:若询问的另外一个点已经遍历过(回溯完成),那么该点将被分到一个集合中,集合的代表点就是两点的最近公共祖先
比如上图,当前正在遍历x这个点,已经遍历完的点为绿色部分,这些点所属集合的代表点位于红色分支上
模板:
// 用dfs维护dis数组
void dfs(int x, int fa)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (y != fa)
{
dis[y] = dis[x] + w[i];
dfs(y, x);
}
}
}
// tarjan处理询问
void tarjan(int x)
{
st[x] = 1; // 当前正在遍历该点
for (int i = h[x]; i != -1; i = ne[i])
{
int y = e[i];
if (!st[y]) // 当前为遍历ydian
{
tarjan(y);
p[y] = u;
}
}
for (auto item : query[x]) // 处理有关当前节点的询问
{
int y = item.first, id = item.first; // id为该询问的唯一编号
if (st[y] == 2) // 询问的另一点已经遍历过
{
int anc = find(y); // 找到集合的代表点,公共祖先
res[id] = dis[x] + dis[y] - 2 * dis[anc]; // 根据id将答案存储到数组中
}
}
st[x] = 2; // 当前节点遍历完
}
板子题:1172. 祖孙询问
由于树的层数最大有40000层,所以一个节点最多向上跳 l o g 400000 log400000 log400000层,大概是一个大于 2 15 2^{15} 215小于 2 16 2^{16} 216的数,所以最多跳 2 16 − 1 2^{16} - 1 216−1层,二进制位取15即可
#include lca或tarjan:1171. 距离
与上题一样,题目要处理很多询问,可以用lca或者离线tarjan解决
树的最短路问题可以从公共祖先的角度考虑,假设x和y的公共祖先为t, d i s ( t ) dis(t) dis(t)为根节点到t的距离,那么x和y之间的最短距离就是 d i s ( x ) + d i s ( y ) − 2 ∗ d i s ( t ) dis(x) + dis(y) - 2 * dis(t) dis(x)+dis(y)−2∗dis(t)
题目没有给定根节点,我们任意指定一个点为根节点即可
lca解法:
#include tarjan解法:
#include debug:维护的query信息要不同地插入两次
query[x].push_back({y, i});
query[y].push_back({x, i});
因为当前询问有关x的信息时,y可能没有遍历完,但是询问y有关的信息时,x是遍历完的
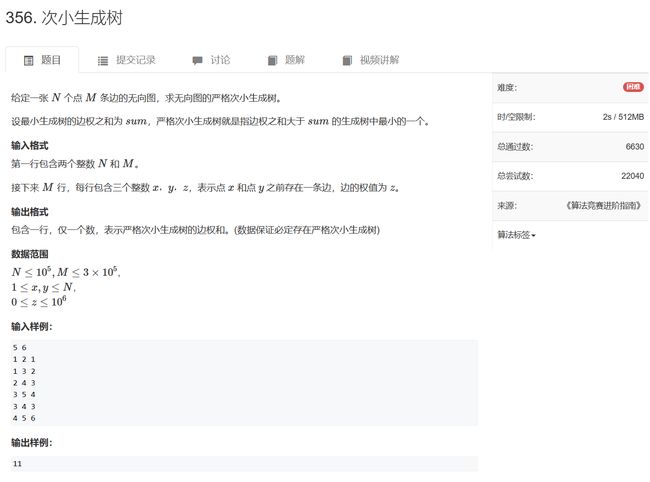
356. 次小生成树
d 1 ( i , j ) d1(i, j) d1(i,j)表示从i往上跳 2 j 2^j 2j层后,路径上的最大边权
d 2 ( i , j ) d2(i, j) d2(i,j)表示从i往上跳 2 j 2^j 2j层后,路径上的次大边权
跳 2 j 2^j 2j步是一个类似分治的过程,分成两部分跳,这两部分依旧能分成两部分跳
路径上的最大值为每一段的最大值取max,次大值为所有子路径的最大值和次大值中的第二大,每次遍历子线段时维护信息即可
if (d > d1) d2 = d1, d1 = d;
else if (d != d1 && d > d2) d2 = d;
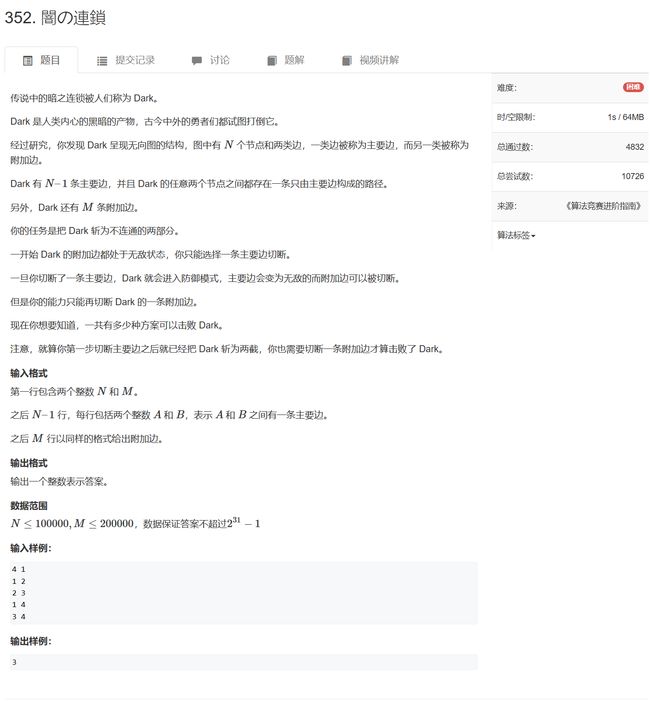
#include 352. 闇の連鎖
树上差分,将x到y的最短路径上所有的边加上c,若p为x和y的公共祖先,那么
d(x) += c, d(y) += c, d(p) -= 2c
如何计算某条边的权值?以这条边的子节点为根的子树中,所有边的权值相加为这条边的权值
在一颗树中,删除任意一条边,那么这颗树将被切成两个连通块
若向树中再添加一条边,那么这条非树边和树边就一定构成环,要向将此时的“树”切成两个连通块,就要删除环中的任意一条树边与这条非树边
题目限制只能先切树边,再切非树边,一共两次,两次过后还没有切成两个连通块,说明这个方案行不通
当切除树边,不用再切除非树边就得到两个连通块时,由于题目限制,还需要切除一条非树边,假设非树边有m条,那么此时可以选择m条边中的任意一条切除,此时的方案数为m
若切除树边后,还要再切除一条非树边,才能得到两个连通块时,此时的方案数为1,只能切除这条环中的非树边
若切除树边后,还要再切除大于一条的非树边,此时无法再切除,方案数为0
现在的问题是,如何知道切除某条树边后,还需要再切除几条非树边?
假设现在已经用树边建立了一棵树,此时再添加非树边将构成环,将环中的所有树边权值加1,假设初始权值为0,此时可以使用树上差分
然后遍历所有的树边,根据边权计算方案数
#include