算法学习之算法效率分析

算法效率分析基础

输入规模的度量

几乎所有的算法，对于规模更大的输入都需要运行更长的时间。例如，需要更多时间来对更长的数组排序，更大的矩阵相乘也需要花费更多时间，等等。所以，使用一个以算法输入规模式n为参数的函数，来研究算法效率是非常合乎逻辑的。

运行时间的度量单位

• 统计算法每一步操作的执行次数——不可行。

• 统计算法中最重要的操作—基本操作的执行次数。

  • 排序的基本操作：比较
  • 矩阵乘法的基本操作：乘法
  • 多项式求值的基本操作：乘法

• 执行次数C(n)是输入规模n的函数，算法运行时间T(n)是执行次数的函数：T(n) ≈ copC(n)
  其中: cop为特定计算机上一个基本操作的执行时间，是常量。

  增长次数

  为什么对于大规模的输入要强调执行次数的增长次数呢？这是因为小规模输入在运行时间上差别不足以将高效的算法和低效的算法法区分开来

算法的最优、最差和平均效率

• 一个算法的最差效率是指当输入规模为n时，算法的最坏情况下的效率。这时，相对于其他规模为n的输入，该算法的运行时间最长。
• 一个算法的最优效率是指当输入规模为n时，算法在最优情况下的效率。这时，与其它规模为n的输入相比，该算法运行得最快。
• 然而，无论是最差效率分析还是最优效率分析都不能提供一种必要的信息：在“典型”或者“随机”输入的情况下， 一个算法会具有什么样的行为。这正是平均效率试图提供给我们信息。
• 还有一种类型的效率称为摊销效率。它并不适用于算法的单次运行，而是应用于算法对同样数据结构所执行的一系列操作。

分析框架概要

• 算法的时间效率和空间效率都用输入规模的函数进行度量。
• 我们用算法基本操作的执行次数来度量算时间效率。通过计算算法消耗的额外存储单元的数量来度量空间效率。
• 在输入规模相同的情况下，有些算法的效率会的显著差异。对于这样的算法，我们需要区分最差效率，平均效率和最优效率。
• 本框架主要关心，当算法的输入规模趋向于无限大的时候，其运行时间（消耗的额外空间）函数的增长次数。

渐进符号和基本效率类型

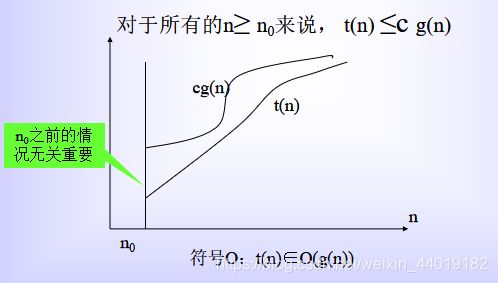
符号О

定义1 我们把函数t(n)包含在O(g(n)) 中，记作t(n) ∈ O(g(n)) ;它的成立条件是：对于所有足够大的n， t(n) 的上界由g(n)的常数倍数所确定，也就是说，存在大于0的常数c和非负的整数n0，使得：

符号Ω

定义2 我们把函数t(n)包含在Ω(g(n))中，记作t(n)∈Ω(g(n))，它的成立条件是：对于所有足够大的n， t(n)的下界由g(n)的常数倍所确定，也就是说，存在大于0的常数c和非负的整数n0，使得：

符号Θ

定义 3我们把函数t(n)包含在Θ(g(n)) 中，记作t(n) ∈ Θ(g(n)) ;它的成立条件是：对于所有足够大的n， t(n) 的上界、下界都由g(n)的常数倍数所确定，也就是说，存在大于0的常数c1，c2和和非负的整数n0，使得：

利用极限比较增长次数

虽然符号O， Ω和Θ的正式定义对于证明它们的抽象性质是不可缺少的，但我们很小直接用它们来比较两个特定函数的增长次数。有一种较为简便的比较方法，它是基于对所计论的两个函数的比率求极限。有3种极限情况会发生：

基本的效率类型

关于渐进时间效率：

• 对规模较小的问题,决定算法工作效率的可能是算法的简单性而不是算法执行的时间

• 当比较两个算法的效率时,若两个算法是同阶的,必须进一步考察阶的常数因子才能辨别优劣。

非递归算法的数学分析

考虑一下从n个元素的列表中查找元素最大值的问题.简单起见,我们假设列表是用数组实现的。下面给出一个解决问题的标准算法的伪代码。

算法  MaxElement(A[0..n-1])
         //求给定数组中最大元素的值
        //输入：实数数组A[0..n-1]
        //输出:A中最大元素的值
        maxval←A[0]
        for i←1 to n-1 do
              if A[i]>maxval
                  maxval←A[i]
         return maxval

确定基本操作：是赋值运算还是比较运算?
把C(n)记作比较运算的执行次数,并试图寻找一个公式将它表达为规模n的函数。：

分析非递归算法效率的通用方案

1. 决定用哪个(哪些)参数作为输入规模的度量
2. 找出算法的基本操作（作为一规律，它总是位于算法的最内层循环中）。
3. 检查基本操作的执行次数是否只依赖输入规模。如果它还依赖一些其他的特性，则最差效率、平均效率以及最优效率（如果必要）需要分别研究。
4. 建立一个算法基本操作执行次数的求和表达式。
5. 利用求和运算的标公式和法则来建立一个操作次数的闭合公式，或者至少确定它的增长次数。

考虑一下元素惟一性问题：验证给定数组中的元素是否全部惟一。

下面这个简单直接的算法可以解决该问题。

算法  UniqueElements(A[0..n-1])
//验证给定数组中的无素是否全部惟一
//输入：数组A[0..n-1]
//输出：如果A中的元素全部惟一，返回“true”
//            否则，返回“false”.
 for i←0 to n-2 do
       for j←i+1 to n-1 do
            if A[i]=A[j] return false
Return true

这个结果是完全可以预测的：在最坏的情况下，对于n个元素的所有n(n-1)/2对两两组合，该算法都要比较一遍。

计算两个n阶方阵乘积的例子

算法伪代码：
MaxtrixMultiplication(A[0..n-1,0..n-1],B[0..n-1,0..n-1])
    for i=0 to n-1 do
       for j=0 to n-1 do 
          C[i,j]=0.0
          for k=0 to n-1 do
           C[i,j]=C[i,j]+A[i,k]*B[k,j]
    return C

分析：

• 输入规模的度量：n
• 基本操作：乘法
• 执行次数表达式

M(n)=

• 运行时间：T(n)≈CmM(n)∈Θ(n3)
  其中Cm为执行一次乘法在某计算机上所需要的时间
• 若考虑加法，则
  T(n)≈CmM(n)+CaA(n)∈Θ(n3)
• 其中Ca为执行一次加法在某计算机上所需要的时间，A(n)为加法的执行次数。

递归算法的数学分析

对于任意非负整数n,计算阶乘函数F(n)=n!的值。因为
当n≥1时，n!=1·…·(n-1)·n=(n-1)!·n

      并且根据定义，0!=1，我们可以使用下面的递归算法       计算F(n)=F(n-1)·n
 算法  F(n)
      //递归计算n!
      //输入：非负整数n
      //输出：n!的值
         if n=0 return 1
         else return F(n-1)*n
       我们用n本身来指出算法的输入规模（而不是它的二进制表示的比特数）。该算法的基本操作是乘法，我们把它的执行次数记作M(n)。因为函数F(n)的计算是根据下面公式：
           当n>0时，F(n)=F(n-1)*n

所以，计算这个公式时，用到的乘法数量M(n)需要满足这个等式：
当n>0时，M(n)=M(n-1)+1

​ 的确，计算F(n-1)需要用M(n-1)次乘法，还有一次乘法用来把该结果乘法n。为了确定一个惟一解，我们还需要一初始条件来告诉我们该序列的起始值。为了得到这个起始值，我们可以观察该算法停止递归调归调用时的条件：if n=0 return 1 所以，我们所遵循的初始条件是：
​ M(0)=0

这样，我们成功地建立了关于该算法的乘法次数M(n)的递推关系和初始条件：
当n>0时，M(n)=M(n-1)+1
M(0)=0
最终结果为 M(n)=M(n-1)+1=…=M(n-i)+i=…=M(n-n)+n=n

递归的思路

• 实际上, 递归思路是把一个不能或不好直接求解的“大问题”转化成一个或几个“小问题”来解决,再把这些“小问题”进一步分解成更小的“小问题”来解决,如此分解,直至每个“小问题”都可以直接解决(此时分解到递归出口)。
• 但递归分解不是随意的分解,递归分解要保证“大问题”与“小问题”相似,即求解过程与环境都相似。并且有一个分解的终点。从而使问题可解。

分析递归算法效率的通用方案

1. 决定用哪个（哪些）参数作为输入规模的度量。
2. 找出算法的基本操作。
3. 检查一下，对于相同规模的不同输入，基本操作的执行次数是否不同。如果不同，则必须对最差效率、平效率以及最优效率作单独研究。
4. 对于算法基本操作的执行次数，建立一个递推关系以及相应的初始条件。
5. 解这个递推式，或者至少确定它有解的增长次数。

汉诺塔（Tower of Hanoi）问题

盘子移动时必须遵守以下规则：

• 每次只能移动一个盘子；
• 盘子可以插在A,B和C中任一塔座；
• 不能将一个较大的盘子放在较小的盘子上。

分析：

输入规模：盘子的数量
记M(n) 为移动盘子的次数，则递归关系式
M(n)=M(n-1)+1+M(n-1)
M(1)=1
解该递归关系可得
　　　 M(n)=2n-1

这是个指数级的算法，是算法不好吗？
对这个问题而言，它是一个高效的算法．

斐波那契数列

斐波那契数列—0,1,1,2,3,5,8,13,21,34,…
这个数列可以用一个简单的递推式和两个初始条件来定义：
当n>1时，F(n)=F(n-1)+F(n-2)
F(0)=0,F(1)=1

算法 F(n)
//根据定义，递归计算第n个斐波那契数
//输入：一个非负整数n
//输出：第n个斐波那契数
    if n≤1 return n
    else return F(n-1)+F(n-2)

该算法的基本操作很明显是加法，我们把A(n)定义为这个算法在计算F(n)的过程中所做的加法次数。因而，计算F(n-1)和F(n-2)所需要的加法次数分别是A(n-1)和A(n-2)，而该算法还需要做一次加法来计算它们的和。因此，对于A(n)我们有下面的递推式：
当n>1时，A(n)=A(n-1)+A(n-2)+1
从递推式中，我们可以预计到该算法的效率不高。的确，它包含两个递归调用，而这两个调用的规模仅比n略小一点。通过观察该算法的递归调用树，我们也能发现该算法效率低下的原因。相同的函数值被一遍一遍地重复计算，这很明显是一种效率低下的做法。

通过简单地对斐波那契数列的连续元素进行迭代计算，我们得到了一个快得多的算法，就像下面的这个算一样：

算法  Fib(n)
//根据定义，迭代计算第n个斐波那契数
//输入：一个非负整数n
//输出：第n个斐波那契数
  F[0]←0;F[1]←1
  for i←2 to n do 
        F[i]←F[i-1]+F[i-2]
  return F(n)

很明显，这个算法要做n-1次加法运算。所以，它和n一样都是线性函数，“仅在”作为n的二进制位数的函数时，才表现为指出级函数。注意，没有必要特意使用一个数组在存储斐波那契数列的前面元素：为了完成该任务，只需要存储两个元素就足够了。