GC复制算法
原理篇
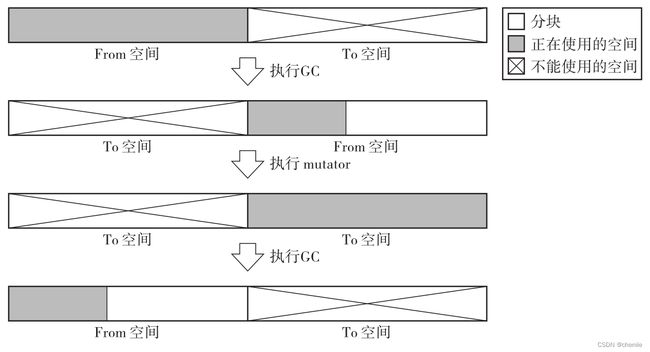
GC复制算法的思路是将堆一分为二,我们暂时叫它们A堆和B堆。申请内存时,我们统一在A堆分配,当A堆用完了,我们将A堆中的活动对象全部复制到B堆,然后A堆的对象就可以全部回收了。这时我们不需要将B堆的对象又搬回A堆,只需要将A和B互换以下就行了,这样原来的A堆变成B堆,原来的B堆变成了A堆。经过这一轮复制,活动对象搬了新家,垃圾也被回收了。GC复制算法就是在两个堆之间来回倒腾。
说到复制,我们脑海中应该马上浮现出另一个词:重写指针。由于对象地址发生了变化,GC复制算法在复制过程中还需要重写指针。
从复制的角度来看,活动对象是从A堆复制到B堆。因此我们也将A堆称为From空间,将B堆称为To空间。
经过复制,原本散落在From空间中的活动对象被集中放到了To空间开头的连续空间内,这一过程也叫做压缩。看下图。
复制过程的伪代码如下:
//将From空间的活动对象复制到To空间
copying() {
$free = $to_start //$free指向To空间中未被使用内存的起始位置
for(r : $roots) //遍历活动对象
*r = copy(*r) //复制活动对象并重写指针
swap($from_start, $to_start) //互换From空间和To空间
}
//将obj及其子对象从From空间复制到To空间
copy(obj) {
if(obj.tag != COPIED) //未复制
copy_data($free, obj, obj.size) //将obj复制到$free指向的地址
obj.tag = COPIED //标记对象已复制,防止重复复制
obj.forwarding = $free //记录复制对象的新地址
$free += obj.size //跳过obj占用的空间
//遍历obj的子对象,注意这里用的是obj.forwarding,
//因为我们要重写指针,所以必须遍历复制后的对象的子对象,
//而不是遍历的obj的子对象
for(child : children(obj.forwarding))
*child = copy(*child) //复制子对象并重写指针
return obj.forwarding //返回复制后对象的新地址
}
整个复制过程就是图的深度优先遍历过程,obj.tag用来防止重复遍历。其中有几个细节我们要注意一下。
首先是copy函数需要返回复制后对象的新地址,因为我们要用这个新地址来重写指针。
其次我们在原对象中也记录了复制后的新地址,这一点很重要。比如对象A和B相互引用,A复制完以后,下一个要复制B,B复制完以后又要复制A,但此时A已经复制过了,不会再复制了。如果我们不事先记录下A的新地址,这里就没法重写新B对象中指向A的地址了。
最后是在递归复制子对象时,我们选择遍历的是新对象的子对象。原因也是我们需要重写指针,而且是重写新对象中的指针,不是原对象的。
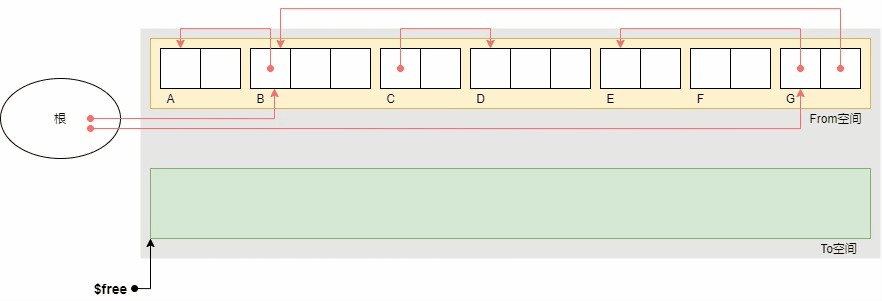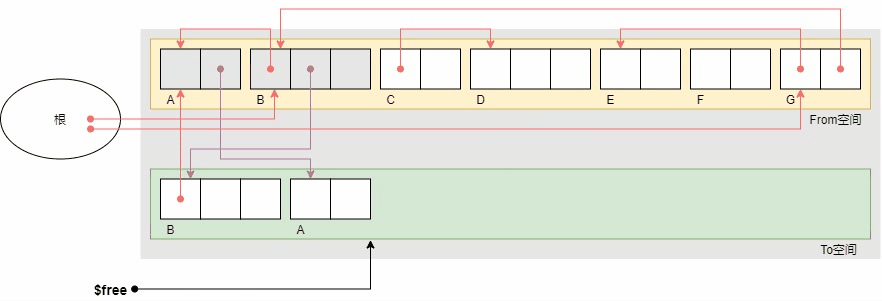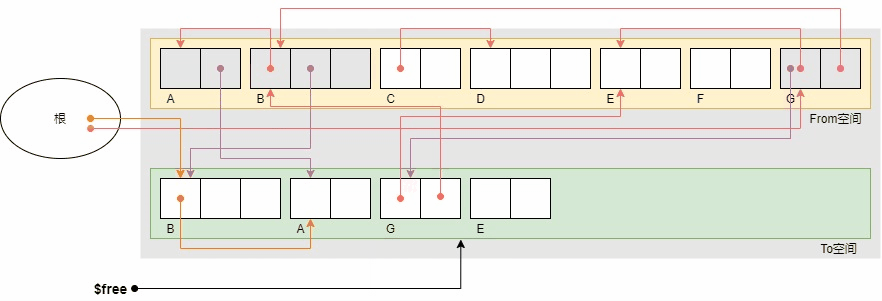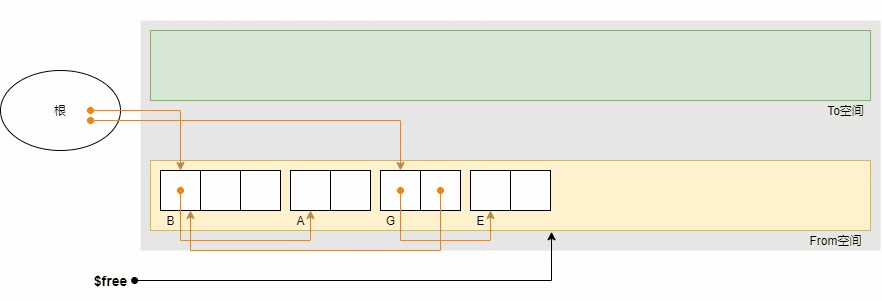
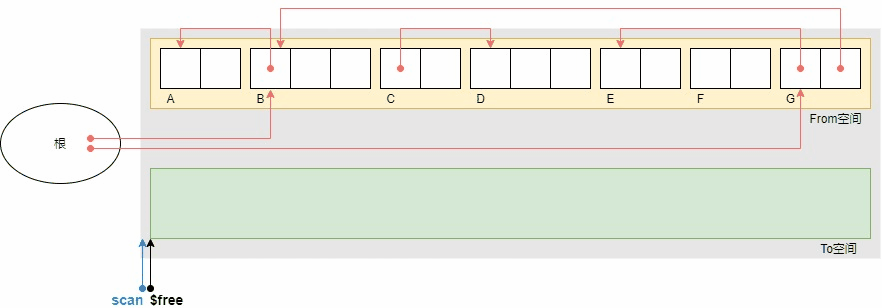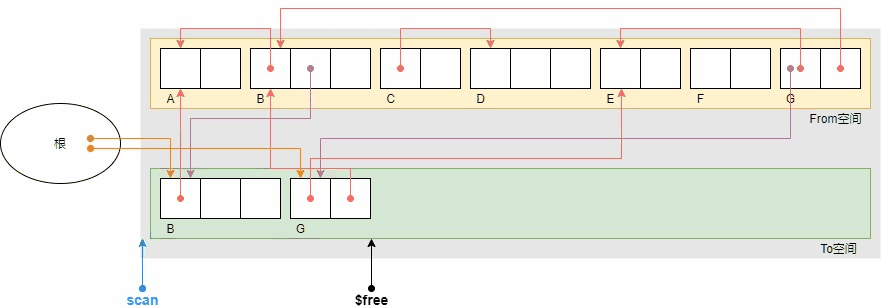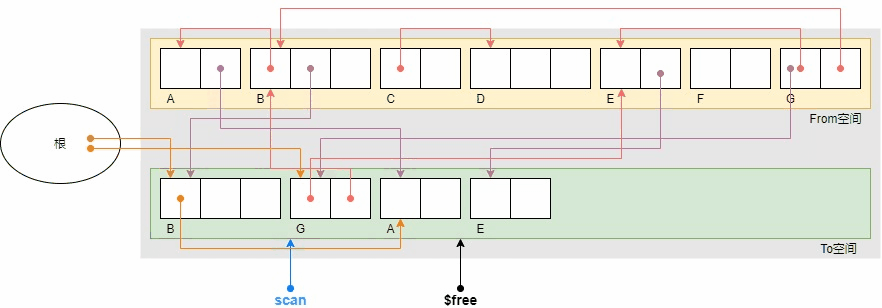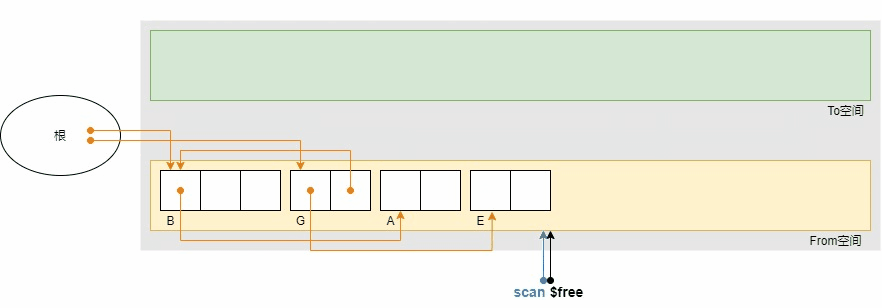
下面的示例显示了复制的执行过程。初始状体下根引用B和G,对象B引用A,对象G引用E和B。
上图中,对象变灰表示obj.tag = COPIED标记,紫色箭头表示obj.forwarding指针,红色箭头表示原对象的引用关系,橙色箭头表示复制对象之间的引用关系。复制结束后,From空间中只剩下活动对象B,A,G和E。
想象一下,如果堆无限大,你会如何分配内存呢。最简单的方式是记录下已使用空间的地址,每次直接往后分配足够大小的空间就行了,这也是最快的方式,因为只需要O(1)的时间复杂度。GC复制算法的分配过程就是这样,因为复制的过程也会进行空间压缩,我们可以假设有无限大的堆。
GC复制算法的分配过程伪代码如下:
new_obj(size) {
//剩余空间不足size
if($free + size > $from_start + HEAP_SIZE/2)
copying() //垃圾回收
//剩余空间仍不足size
if($free + size > $from_start + HEAP_SIZE/2)
allocation_fail() //分配失败
obj = $free //从$free处开始分配
obj.size = size //设置对象大小
$free += size //分配size大小的内存
return obj
}
GC复制算法必须将堆分成大小相等的两份,$free始终指向可用内存的起始位置。请看下图。
上图中灰色部分表示已用空间,白色表示可用空间。
GC复制算法的优点如下:
- 吞吐量优秀。这得益于GC复制算法只会搜索复制活动对象,能在较短时间内完成GC,而且时间与堆的大小无关,只与活动对象数成正比。相比于需要搜索整个堆的GC标记清除算法,GC复制算法吞吐量更高,而且堆越大,差距越明显。
- 分配速度快。因为不需要搜索空闲链表,在O(1)的时间复杂度就能完成分配。
- 不会发生碎片化。因为每次复制都会执行压缩。
- 与缓存兼容。因为复制过程中使用了深度优先遍历,具有引用关系的对象会被复制到相邻的位置,局部性原理可以很好发挥作用。
GC复制算法的缺点也是相当明显:
- 堆的使用效率低。这是一个最显眼的问题,因为要留一半的空间用来复制,所以堆的利用率总小于50%。
- 不兼容保守式GC。因为GC复制算法需要移动对象。
- 复制时存在递归调用,需要消耗栈空间,并可能导致栈溢出。
缺点中除了第二点,第一点和第三点都有优化的空间。
优化篇
广度优先搜索
将复制过程中的深度优先搜索换成广度优先搜索,从而将递归调用变成迭代算法。由C. J. Cheney于1970年发明,也称为Cheney的GC复制算法。这个名字怪怪的,所以我们暂且叫它广优的GC复制算法吧。
一般广度优先搜索需要一个队列来辅助,也需要占用额外的内存空间。但可巧的是,当我们把对象复制到To空间之后,To空间就天然成为了一个队列,这也是该算法的巧妙之处。
复制过程伪代码如下。
//将活动对象从From空间复制到To空间
copying() {
//scan指向队首,$free指向队尾
scan = $free = $to_start
for(r : $roots) //遍历根直接引用的对象
*r = copy(*r) //复制对象并重写指针,此过程也是在入队
while(scan != $free) //队列不为空
for(child : children(scan)) //遍历队头对象的子对象
*child = copy(*child) //复制子对象并重写指针,也是在将子对象入队
scan += scan.size //出队
swap($from_start, $to_start) //交换From和To空间
}
//将obj复制到To空间
copy(obj) {
//判断obj是否复制过,如果obj已复制过,
//那么obj.forwarding必然指向To空间
//否则obj.forwarding应该是空指针
if(is_pointer_to_heap(obj.forwarding, $to_start) == FALSE)
copy_data($free, obj, obj.size) //将obj复制到$free指向的内存
obj.forwarding = $free //记录复制后对象的新地址
$free += obj.size //跳过obj占用的空间
return obj.forwarding //返回复制对象的新地址,用于重写指针
}
算法应该不难理解,此时To空间也承担了队列的作用,scan表示队首,$free表示队尾,copy函数其实就是将对象入队。同时这里也取消了obj.tag字段,而是通过forwarding指针指向的位置来判断对象是否已被复制过。不得不说,确实巧妙。
还是之前的示例,广优的复制过程如下。
广优的GC复制算法的优点是避免了递归带来的栈消耗。但同时也带来了一个缺点,广度优先搜索使得具有引用关系的对象被复制到了相聚较远的位置,因为节点和祖父节点之间还隔着一群叔父节点,从示例中复制完成后B,A,G,E的相对位置也能看出,因此也在一定程度上抵消了局部性原理的优势。
近似深度优先搜索
对于近似深度优先遍历书中只举了一个非常特殊的例子,没有关于算法细节的描述,只能大概了解下思路。
近似深度优先搜索是为了优化标准广度优先搜索无法有效利用局部性原理的问题。这里我们先引入"页"这样一个单位。CPU一般会按页读取内存,因此我们只要把具有引用关系的对象放在一个页内,那么也可以有效利用局部性原理。
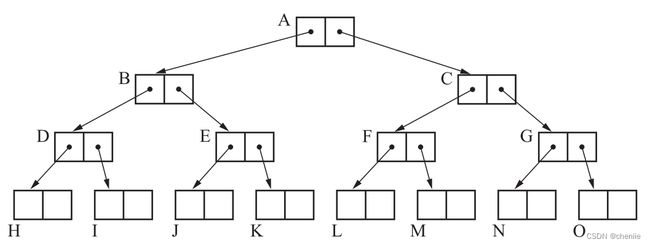
考虑下面这样一颗二叉树,每个对象占2个字。
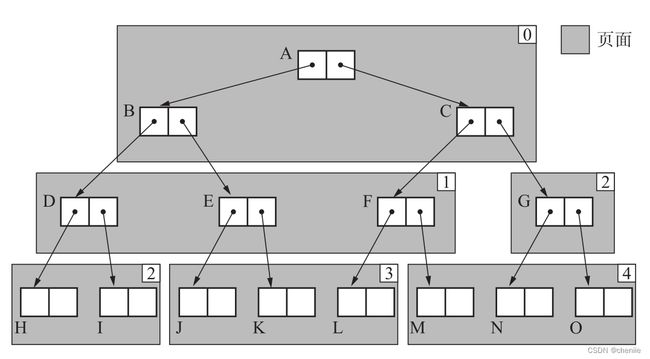
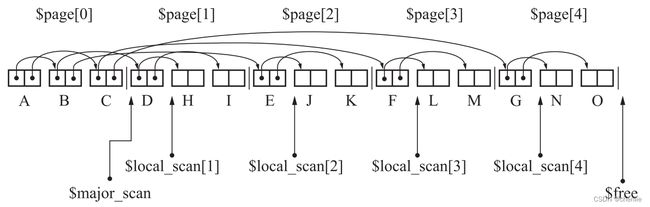
假设页面大小为6个字,那么标准广度优先搜索会将对象在页中摆放如下。
上图中,灰色表示页,右上角是页的编号,编号从0开始。广度优先搜索的遍历顺序是ABCDEFGHIJKLMNO,因此ABC被放到了0号页,也就是第一页。DEF被放到了1号页,GHI被放到了2号页,JKL被放到了3号页,MNO被放到了4号页。
可以看到越靠近叶子节点,同一个页内的对象越不具备引用关系。因为广度优先是按层遍历,被分到同一页的对象最有可能是兄弟关系,而不是父子关系。
近似深度优先搜索使用了下面4个全局变量:
$page:记录页的数组,$page[i]指向第i个页的开头。$local_scan:每个页面的scan变量,$local_scan[i]指向第i个页面中下一个应该搜索的对象。$major_scan:指向还未搜索完的页的开头。$free:指向堆的可用空间开头。
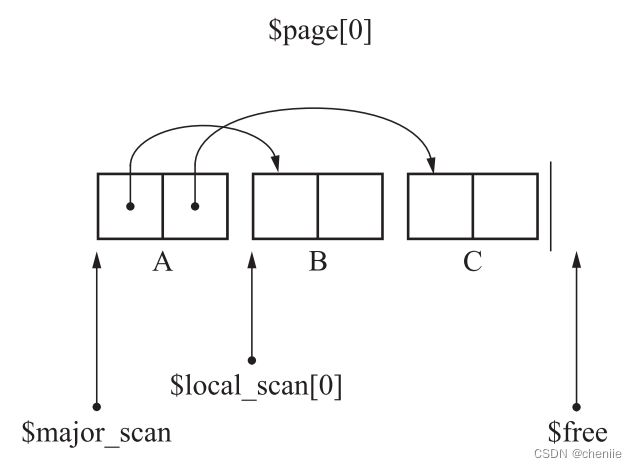
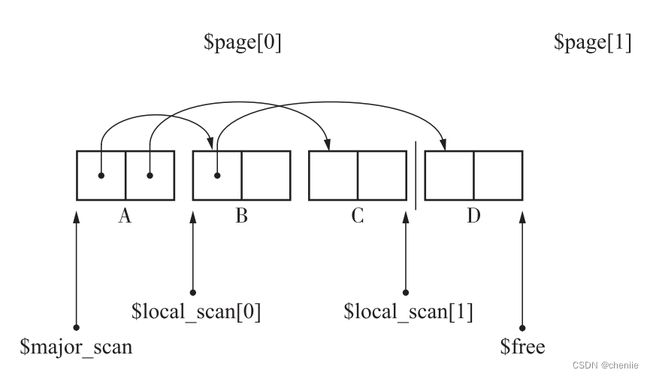
按上图给出的示例,首先将对象A复制到To空间,然后搜索A,将A引用的B和C复制到To空间,于是ABC被复制到第0页。A已搜索完毕,$local_scan[0]指向下一个对象B。
此时$free处于1号页的开头,接下来被复制的对象会被安排到新页面。对于这种情况,我们从$major_scan指向的页的$local_scan处开始搜索。而当对象被复制到新页面时,我们会从当前页面的$local_scan处开始搜索,直达页面被填满。
这一段优点绕,我们用示例来说明。此时$free到达了一个新的页面,于是我们回到$major_scan指向的页面,也就是0号页面的$local_scan处,也就是$local_scan[0]的位置继续搜索,所以我们应该搜索B对象。首先将B对象引用的D复制到$free处。
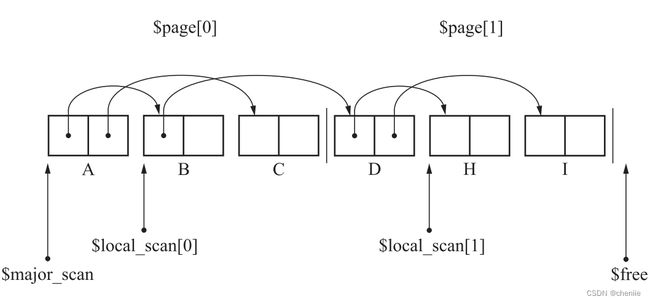
这是因为有对象被复制到新页面,所以我们应该从当前页面的$local_scan也就是$local_scan[1]的位置开始搜索,所以现在应该搜索对象D,将D引用的H和I复制过来。
此时1号页已填满,$free又指向了新页面,于是我们又回到$major_scan页,也就是继续从$local_scan[0]处搜索。$local_scan[0]还指向B,所以我们继续搜索B,这次将B引用的E复制过来。
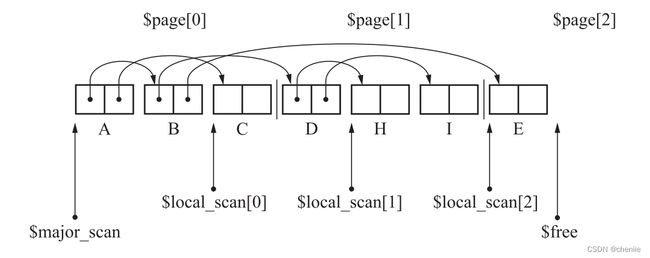
此时B搜索完,我们将$local_scan[0]指向C。由于E被复制到了新页面,和D的情况一样,我们再次放弃对$local_scan[0]的搜索,转而搜索$local_scan[2],也就是对象E,将它子对象J和K复制过来。
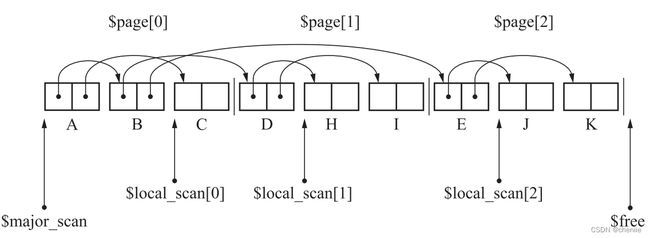
这时2号页被填满,$free到了3号页的开头。于是我们再次回到$major_scan页,继续对#local_scan[0]进行搜索。整个过程执行完以后如下图所示。
此时还没结束,$major_scan才到达2号页,但是后面的过程就只是移动指针而已,不会再复制对象,因为所有对象都已经复制完了。
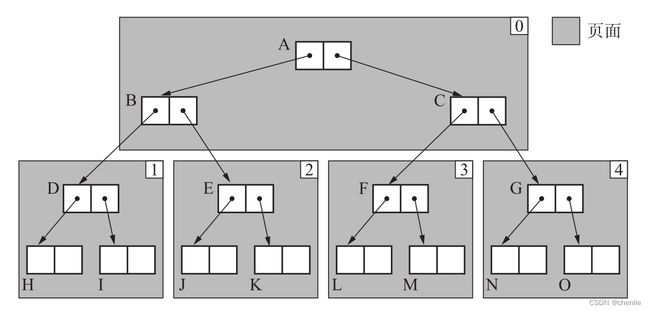
经过近似深度优先搜索的复制,对象与页面的关系如下图。
可以看到,每个页面内的对象都存在引用关系,相比于普通广度优先搜索能更好利用局部性原理。
近似深度优先搜索虽然名字里有个"深度",但其实它还是广度优先搜索,只不过近似深度优先搜索有两个队列。首先是整个堆作为一个队列,队列元素是页,队首是$major_scan,队尾是page[N-1](假设一共N个页),这是第一个队列。其次是每个页内形成一个队列,队列元素是对象,队首是$local_scan[i],队尾是page[i]+page_size,这是第二个队列。对于每个队列来说其实都是广度优先遍历,只不过我们在$major_scan和当前页之间来回切换使得算法看起来略显复杂,也正是这种切换,保证了每个页内的对象尽量是具有引用关系的。
多空间复制
多空间复制针对的是GC复制算法不能有效利用堆的问题。它的基本思路是将堆均分成N份,N≥2,然后选取其中2份用来执行GC复制算法,剩下N-2份执行GC标记清除算法,如此一来堆的利用率就从50%上升到了 N − 1 N \frac{N-1}{N} NN−1。
这么直白的嫁接还真实让人意想不到,真不知道是该说结合了两者的优点,还是集合了两者的缺点。
算法伪代码如下:
multi_space_copying() {
//将堆分成N等份,$to_space_index表示用作To空间的那块堆的编号
//$free就是用作To空间的那块堆的起始位置
$free = $heap[$to_space_index]
for(r : $roots) //遍历根直接引用的对象
*r = mark_or_copy(*r) //复制或者标记
for(index : 0..(N-1)) //遍历每块堆空间
if(is_copying_index(index) == FALSE) //第index块堆用的是GC标记清除算法
sweep_block(index) //GC清除阶段
//当前的From空间作为下次GC的To空间
$to_space_index = $from_space_index
//将当前From空间的下一块作为新的From空间
$from_space_index = ($from_space_index + 1) % N
}
//标记或者复制
mark_or_copy(obj) {
//对象OBJ在From空间
if(is_pointer_to_from_space(obj) == TRUE)
return copy(obj) //将obj复制到To空间
else
if(obj.mark == FALSE) //未标记
obj.mark = TRUE //标记为活动对象
for(child : children(obj)) //遍历子对象
*child = mark_or_copy(*child) //递归标记或复制子对象
return obj //返回obj用于重写指针
}
//将obj从From空间复制到To空间
copy(obj) {
if(obj.tag != COPIED) //未复制
copy_data($free, obj, obj.size) //将obj复制到$free处
obj.tag = COPIED //设置已复制标记
obj.forwarding = $free //记录复制对象新地址
$free += obj.size //跳过obj占用空间
for(child : children(obj.forwarding)) //遍历复制对象的子对象
*child = mark_or_copy(*child) 递归标记或复制子对象
return obj.forwarding //返回新对象地址,用于重写指针
}
堆被N等分后,From空间和To空间并不是固定使用某两块堆,每一块堆都会轮流作为From空间和To空间使用。
而且由于GC复制算法和GC标记清除算法的清除阶段都只会访问活动对象,所有我们可以用一个函数mark_or_copy统一处理。这里需要注意在GC标记的代码中也要进行指针重写,因为执行GC标记清除算法的空间中的对象也可能引用到Form空间中的对象。具体是进行标记还是复制取决于对象在不在From空间。
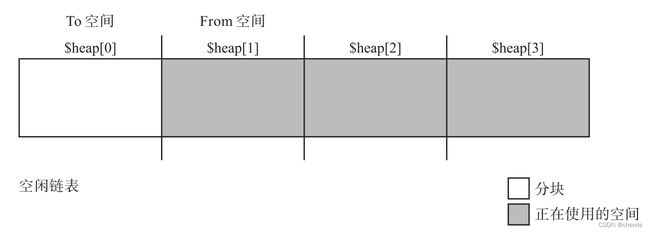
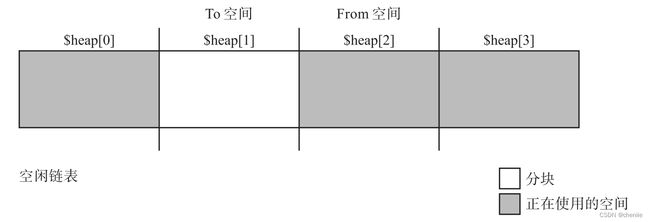
假设我们将堆分为4份,初始状态如下图。
此时执行GC,堆的状态变成下图。
$heap[1]的活动对象压缩到了$heap[0],$heap[1]变成了To空间,$heap[2]成为了From空间。注意此时全局变量$free还是指向$heap[0]的,所以分配对象时要么从$heap[0]分配,要么从空闲链表分配。
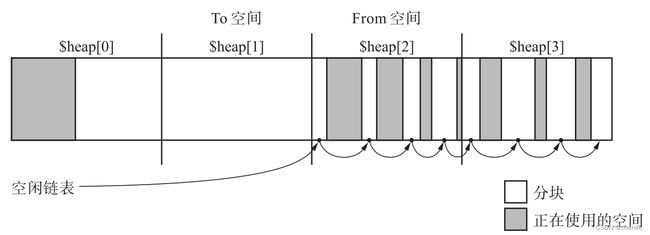
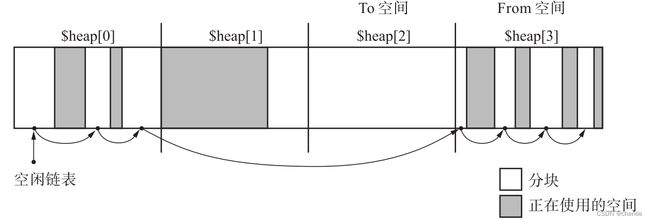
随着程序执行,堆再次用完,如下图。
此时再次执行GC,堆的状态变成下图。
$heap[2]的活动对象压缩到了$heap[1],$heap[0]和$heap[3]分别执行了GC标记清除算法。
相比于GC复制算法,多空间复制提高了堆的利用率。但同时也引入了GC标记清除算法的一些缺点,将堆划分成多少份就成了我们手里的天平。
总结
- GC复制算法将堆均分为A,B两份,GC时将A堆的活动对象复制到B堆,复制过程中完成重写指针和压缩,复制完后将AB角色互换,由于压缩的存在,拥有极高的分配速度。
- 广优的GC复制算法将复制过程搜索活动对象的深度优先遍历换成了广度优先遍历,消除了递归调用栈的消耗。利用To空间作为天然的队列,也不需要消耗额外的内存空间。
- 近似深度优先搜索方法在To空间构造了两个队列,一个页队列,一个页中对象的队列,对两个队列分别广度优先搜索,将具有引用关系的队列尽量安排在同一个页面,在避免递归调用的同时有效利用了局部性原理。
- 多空间复制算法将GC复制算法和GC标记清除算法结合起来,将堆N等分,其中2份执行GC复制算法,N-2份执行GC标记清除算法,相比于GC复制算法提高了堆的利用率。
更多阅读
-
GC标记清除算法
-
引用计数法
-
GC标记压缩算法
-
渐进式垃圾回收