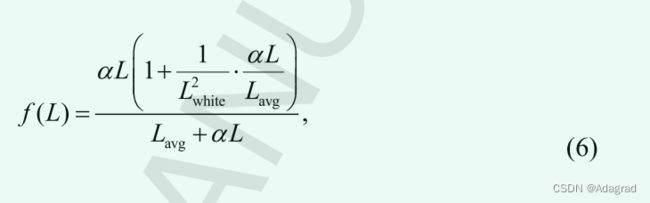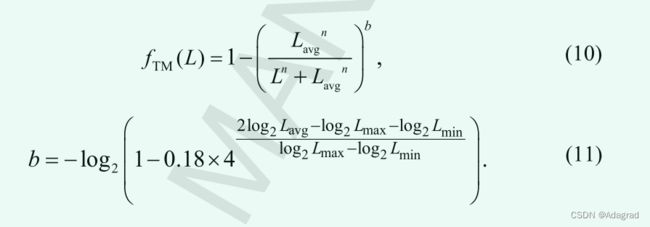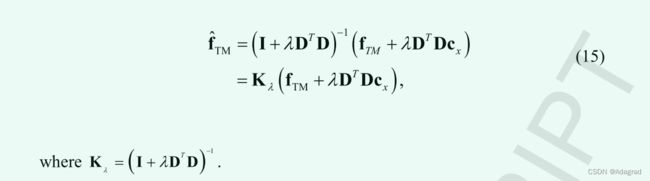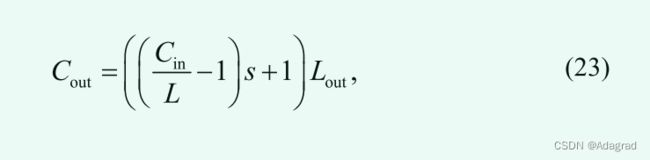High Dynamic Range Image Tone MappingBased on Asymmetric Model of RetinalAdaptation

Abstract

使用对称视网膜对光响应模型的全局色调映射算子往往会产生低动态范围 (LDR) 图像，该图像在明亮或黑暗区域中显示出其对应的高动态范围 (HDR) 图像的细节丢失。在本文中，我们基于包含对称 S 形曲线的视网膜适应模型引入了一种新的非对称 S 形曲线（ASC），并利用 ASC 提出了两个全局色调映射算子。在所提出的方法中，通过使用众所周知的经典摄影技术，称为区域系统，获得基于 ASC 的色调映射函数。此外，通过使用输入 HDR 图像的亮度直方图和基于 ASC 的映射函数制定双准则优化问题，引入了对比度增强色调映射函数。实验结果表明，所提出的方法增强了全局对比度，同时保留了色调映射 LDR 图像中的图像细节。此外，使用图像质量度量的客观评估结果表明，所提出的方法对最先进的全局色调映射算子显示出高性能。

1. Introduction

随着高动态范围 (HDR) 技术的快速发展，HDR 图像可以提供远多于 24 位 RGB 图像的亮度和颜色信息 [1]。然而，由于大多数显示设备仍然具有低动态范围 (LDR)，因此已经提出了各种类型的色调映射算子来在 LDR 设备上表示 HDR 图像。这些方法可以大致分为两部分：全局[2]-[10]和局部[11]-[19]算子。

全局色调映射算子对每个像素应用空间不变的压缩函数来压缩 HDR 图像的动态范围。例如，一些量化函数（如伽马函数或对数函数）用于简单地压缩 HDR 图像的动态范围 [4]、[10]。另一方面，局部色调映射算子通过考虑相邻像素的局部信息，在每个像素处利用不同的压缩比来保留输出图像中的细节。例如，杜兰德等人[17] 使用局部边缘保留滤波器将输入的 HDR 图像分解为 HDR 基础层和 LDR 细节层。然后，只有 HDR 基础层被压缩并与 LDR 细节层重新组合。同样，Fattal 等人 [18] 通过使用仅压缩 HDR 图像的大梯度的梯度衰减函数，有效地保留了色调映射 LDR 图像的精细细节。

这两个算子的客观[20]和主观[21]比较表明，全局色调映射算子可以更好地再现全局对比度，但会导致细节信息的丢失。同时，局部色调映射算子具有更好的细节可见性，但与全局算子相比，在降低计算复杂度方面效率较低。此外，局部操作员往往会产生不自然的外观，例如振铃和光晕伪影。

由于人类视觉系统 (HVS) 成功地处理了大范围亮度强度的动态范围问题，许多色调映射操作员采用了各种模拟 HVS 的假设模型。例如，retinex 理论 [22]，它通过使用 HVS 再现对颜色刺激的感官反应，已在许多局部色调映射算子中实施。乔布森等人[11] 引入了多尺度中心/环绕视网膜来产生类似于人类视觉感知的 LDR 图像。 Meylan 和 Süsstrunk [12] 扩展了这种多尺度 retinex，以提供良好的色彩再现并防止色调映射过程中的光晕伪影。此外，Mantiuk 等人[19] 引入了一个感知框架，将 HVS 的特性纳入梯度衰减过程。他们通过采用金字塔对比度表示来重建色调映射图像的低频。然而，这些基于 HVS 的局部色调映射方法通常会受到光晕伪影的影响，并且需要很高的计算复杂度。

由于 Naka-Rushton 方程 [23] 代表了视网膜感光器根据亮度水平的响应，因此被 Pattanaik 等人采用。 [2] 为了重现人眼的时间依赖性视觉适应，已经提出了多种具有 Naka-Rushton 方程的全局色调映射算子。例如，莱达等人[3] 分别将 Naka-Rushton 方程应用于视杆和视锥细胞，以模拟视网膜的局部视觉适应。莱因哈德等人[6] 通过使用一个关键值扩展了 Naka-Rushton 方程，该关键值指示输入的 HDR 图像主观上是亮的、正常的还是暗的。此外，Reinhard 和 Devlin [7] 将色调映射过程与摄影进行了识别，并从类似于摄影师的可变相机设置的可控参数中获得了 Naka-Rushton 方程的色度和亮度适应。最近，费拉丹斯等人[9] 指出了锥饱和的重要性，并结合了 Naka-Rushton 方程和 Weber-Fechner 定律。然而，由于 Naka-Rushton 方程的曲线有一个缺点，即它在半对数坐标上具有对称的 S 形，因此使用 Naka-Rushton 方程的色调映射 LDR 图像往往会丢失其对应 HDR 的细节明亮或黑暗区域中的图像。

在本文中，我们首先在传统的视网膜适应模型的基础上引入了一种新的非对称 sigmoid 曲线（ASC）。受 HVS 特性的启发，其中视网膜响应曲线实际上具有不对称形状 [24]、[25] 并且其对称特性仅在低到中等亮度水平 [26] 中保持，所提出的 ASC 还包括一个不对称参数，该参数确定曲线的曲率。然后，我们提出了一个全局色调映射算子，它通过使用摄影技术确定 ASC 的不对称参数，称为区域系统 [27]。此外，通过将双准则优化问题公式化为两个目标的加权和，提出了对比度增强色调映射函数：一个用于保留基于 ASC 的色调映射函数，另一个用于调整映射函数的斜率就亮度直方图而言。

本文的其余部分安排如下。在第 2 节中，我们介绍了基于传统视网膜反应模型的不对称 sigmoid 曲线。第 3 节详细描述了基于 ASC 的全局色调映射方法。第 4 节介绍了实验结果。最后，第 5 节总结了本文。

2. Proposed asymmetric retinal response model

Michaelis-Menten 方程 [28] 是视网膜适应的常规响应模型，描述了视网膜神经元的典型响应 R 和亮度强度 I 之间的非线性关系，如下所示：

 

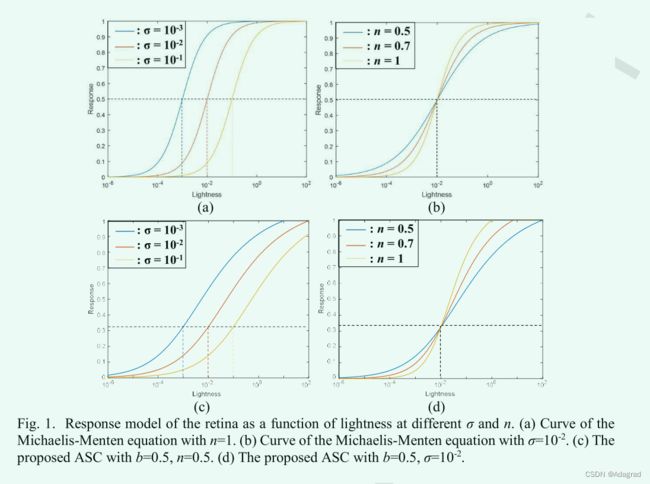
 其中 σ 是表示适应水平的半饱和常数，n 是决定函数陡度的灵敏度参数。参数 Rma​​x 是最大响应，其值通常为 1.0 用于归一化。给定感光器的适应水平 σ 可以被认为是该感光器最近暴露于的光强度的函数，并计算为在静止照明条件下到达整个视场的平均光[7]。请注意，当 I=σ 时，视网膜神经元的响应变为最大值的一半。如图 1(a) 所示，该响应模型在半对数坐标上具有关于其中点 (σ, 0.5) 的对称 S 形。此外，类似于HVS的机制，其中感光器调整对背景照明条件的适应，随着适应水平的增加，Michaelis-Menten方程的曲线沿水平轴从左到右移动。图 1(b) 显示它显着压缩了场景中的明暗区域，而中间范围随着灵敏度参数的增加保持不变。

尽管 Naka-Rushton 方程是 Michaelis-Menten 方程的特例 (n=1)，已在色调映射文献中广泛使用，但该视网膜反应模型的曲线在半对数坐标上具有对称 S 形[29]。为了克服这一限制，我们提出了一种新的 ASC，它包含不对称和对称形状的曲线。

最近，为了从剂量反应数据中找到最佳拟合曲线，Gottschalk 和 Dunn [30] 采用了一种称为 5PL 函数的不对称 sigmoid 曲线，定义为

 其中x表示输入数据，a、b、c、d和n是用于确定函数曲线形状的五个参数。由于视网膜反应在没有光的情况下变为零，即 R(0)=0，我们从 (2) 获得 a=0。因此，（2）可以重写为

 当 b=1 时，ASC 在半对数坐标上具有关于其中点 (σ, 0.5) 的对称 S 形；否则，它变得不对称。随着参数 σ 的增加，ASC 从左向右移动，如图 1（c）所示。比较图1（b）和（d），随着参数n的增加，ASC在点（σ，1-0.5b）附近具有陡峭的斜率，类似于Michaelis-Menten方程的曲线。

如上一节所述，我们设计了 ASC 来获得全局色调映射函数。因此，困难在于确定如何根据 HDR 场景适当地选择不对称参数 b。下一节将解释图像自适应参数估计方法。

3. Proposed tone mapping operators

3.1. ASC-based tone mapping operator

控制照片最终外观的区域系统技术 [27] 用于确定输入 HDR 图像的 (5) 中的不对称参数 b。区域系统将一个场景在色调尺度上划分为 11 个区域，每个区域从纯黑色到纯白色都进行了适当的匹配。在这些区域中，V 区代表 18% 的中灰，通常用作标准灰卡。

在 [6] 中，区域系统与 Naka-Rushton 方程的修改版本一起使用，用于将 HDR 场景转换为 LDR 图像，如下所示：

 其中 f (∙) 是映射函数； α表示键值； L 和 Lavg 分别是输入 HDR 图像的亮度和对数平均亮度； Lwhite 表示映射到纯白色的最小亮度值，例如，对于 8 位 LDR 图像，为 255。 HDR 图像的亮度 L 是通过对输入 HDR 图像的三个颜色通道的值进行加权平均获得的，如下所示：

 在(9)中，由于k的范围是[-1,1]，所以参数α在[0.045,0.72]的范围内。这里，重要的问题是，在经典区域系统中，区域 III 和区域 VII 的适当反射率分别约为 4.5% 和 72%。因此，我们可以得出结论，如果 Lwhite=1，Reinhard 全局色调映射曲线总是经过一个点 (Lavg, α)，而关键值 α 表示以 k 表示的 Zone III 和 Zone VII 之间的反射率值。如图 1(d) 所示，提出的 ASC 总是通过点 (σ, )。此外，如上一节所述，适应水平 σ 通常计算为对数平均亮度。因此，我们设置 σ = Lavg 并将从区域系统获得的点 (Lavg, α) 与 ASC 上的点 (σ, ) 相等。换言之，非对称参数b由以下等式确定：。最后，基于 ASC 提出的色调映射函数 由下式获得

 

 在最近的一项工作 [9] 中，亮度值的算术平均值和中位数之间的几何平均值比对数平均亮度更能代表背景亮度。因此，我们计算背景强度：（10）和（11）中的 。

3.2. Contrast-enhancing tone mapping operator

在本节中，我们提出了一种通过使用（10）中基于 ASC 的色调映射函数和输入 HDR 图像的亮度直方图来生成对比度增强色调映射函数的方法。沃德等人[8] 首先采用亮度直方图的累积分布作为全局色调映射函数。生成的色调映射 LDR 图像显示出类似于直方图均衡 LDR 图像的增强对比度。然而，基于直方图的全局色调映射算子往往会丢失 HDR 图像在明亮或黑暗区域的细节 [32]。尽管局部色调映射算子可以增强局部对比度和细节的可见性，但它需要很高的计算复杂度，如第 1 节所述

为了解决这个问题，我们提出了一个具有两个目标的优化问题：保持上一节中描述的基于 ASC 的色调映射函数的形状，并根据HDR 图像累积分布函数 (CDF) 调整目标映射函数的斜率。这个双准则优化问题可以表述为

 

 

 在 (12) 中，CDF 的斜率 Dcx 等于输入 HDR 图像的概率分布函数。此外，我们最小化目标映射曲线的斜率与 Dcx 之间的差异，而不是绝对差异。这种策略对于只改变目标映射曲线的斜率而不改变 ASC 的形状很有用。我们将在本节末尾展示所提出的优化策略的有效性。

hx为列向量，hx第i个元素为i到i+1区间像素个数，i是以log域等分划分，然后归一化 。

 

 

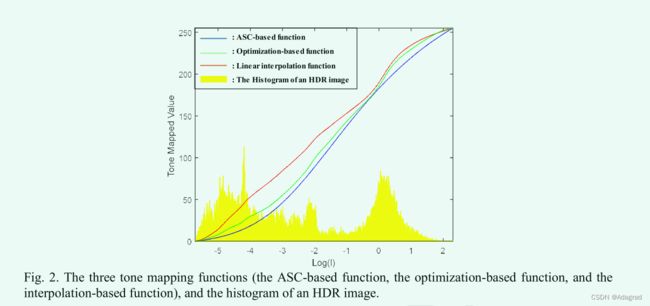
 在所提出的方法中，基于 ASC 的映射函数通过解决优化问题而不是简单的插值方法与 CDF 相结合。图 2 显示了使用优化策略和插值方法的色调映射函数。基于插值的色调映射函数由下式获得

 

4. Experimental results

4.1. Implementation

在本节中，实施了大量实验来验证所提出的色调映射函数 和 的性能。

在评估所提出的方法之前，将颜色校正的线性公式 [34] 应用于每个颜色通道以进行色调映射中的颜色处理，如下所示：

 其中 C 表示颜色通道之一（红色、绿色和蓝色），Lout 是建议的色调映射算子的输出亮度，s 是颜色饱和度的控制参数。

在实验中，从两个 HDR 图像数据集，即 MPI 和 sIBL 中选择了 40 个测试图像。请注意，MPI 数据集已广泛用于 HDR 色调映射，而 sIBL 数据集包含最新的 HDR 图像，主要覆盖超高分辨率的户外场景，如图 3 所示。

4.2. Subjective evaluation

图 4 显示了所提出的基于 ASC 的色调映射方法在 (10) 中具有不同 b 值的结果。对于色调映射，参数设置为 n=1。如图4（a）所示，所提出的色调映射函数（b = 1）的对称版本倾向于保留暗区的精细细节并去除亮区的纹理。随着 b 减小，色调映射结果变得更暗，如图 4（b）和（c）所示。因此，非对称参数 b 对色调映射 LDR 图像的图像质量具有显着影响。在图 4(d) 中，使用 (10) 计算的参数 b 在结果图像的明亮区域和暗区域的细节保留之间提供了良好的折衷。

与具有 256 个量化级别的 LDR 图像的直方图不同，HDR 图像的亮度值是连续的，并且 HDR 图像的直方图 bin 的数量 N 会影响我们的对比度增强色调映射结果的质量。图 5 显示了所提出的基于 ASC 的色调映射方法对（14）中不同 N 值的结果。由于较小的 N 在直方图生成过程中压缩了更多的 HDR 信息，图 5（a）和（b）表明，使用较小的 N 获得的结果在明暗区域表现出更多的细节损失。否则，使用较大 N 的色调映射算子会生成视觉上合理的图像细节，同时需要高计算复杂度。由于 N = 1000 的色调映射结果与 N = 3000 的结果之间没有显着差异，如图 5（c）和（d）所示，我们将所有实验设置为 N = 1000。

图 6 显示了使用所提出的具有不同 λ 的对比度增强色调映射方法的色调映射 LDR 图像。如第 III-B 节所述，参数 λ 控制色调映射过程中亮度直方图的影响。随着λ的增加，大概率区域附近的色调映射曲线的斜率变得更陡峭，色调映射图像的全局对比度也显着增强。在实验中，参数 λ 和 γ 分别根据经验确定为 400 和 50。

为了与所提出的方法进行性能比较，使用了其他最先进的全局色调映射方法，例如 Drago 方法 [4]、Mantiuk 方法 [5]、两种 Reinhard 方法 [6][7]、Ward 方法 [8 ] 和 Ferradans 的方法 [9]。图 7 显示了我们的两种色调映射方法和 sIBL 数据集的传统全局色调映射方法的结果。在实验中，基于 Naka-Rushton 方程的色调映射结果如图 7（d）和（e）所示。虽然结果在暗区有足够的细节，但它们也出现了低对比度。在传统方法中，Mantiuk 的方法 [5] 在保持全局对比度方面表现最好。然而，可以观察到明亮和昏暗区域中图像细节的可见度较差，如图7（c）所示。相比之下，输入 HDR 图像的重要细节和纹理在所提出的基于 ASC 的色调映射方法的结果中得到了很好的呈现，如图 7(g) 所示。在图 7（h）中，所提出的对比度增强色调映射方法不仅保留了图像细节，而且增强了色调映射 LDR 图像的全局对比度。这种趋势也清楚地显示在图 8 中，它使用了 MPI 数据集。

4.3. Objective evaluation

为了客观评估色调映射结果，采用了两种定量质量评估方法。第一种评估方法[35]使用两个输入图像，一个用于输入 HDR 图像作为参考图像，另一个用于色调映射 LDR 图像作为测试图像。评估结果包括一个失真图，它代表了每个像素的对比度失真误差。失真图的灰色、绿色、红色和蓝色分别表示没有失真、可见对比度损失、对比度反转和对比度放大。此外，每种颜色密度都意味着误差的大小。在图 9 中，我们展示了使用两种建议的色调映射算子和传统方法生成的色调映射 LDR 图像和失真图。如图 9(g) 和 (h) 所示，所提出的两种色调映射方法都比其他方法产生更少的失真。

为了分析数值误差，我们从包含 20 个 sIBL 图像和 20 个 MPI 图像的 40 个色调映射 LDR 图像中提取每个像素的误差值，并计算平均值，如表 1 所示。性能最好的方法是粗体，第二个是斜体。除了关于对比度损失的类别外，两种提出的方​​法都优于其他色调映射方法。在表 I 中，与其他传统方法相比，Ward 方法相对导致较低的损耗和较高的反转以及对比度的放大。此外，与基于 ASC 的色调映射算子相比，增强对比度的色调映射算子在放大和反转类别中产生了更多的错误。由于这两种方法的色调映射结果通常在图 1-2 中表现出增强的对比度。从图 7 和图 8 可以看出，带有亮度直方图的色调映射算子在增强全局对比度的同时，会导致对比度反转和放大的误差。

在第二个实验中，采用了由局部结构保真度测量和统计自然度测量组成的色调映射图像质量指数（TMQI）[20]。该指标给出了 [0, 1] 之间的整体性能得分，其中得分越高表示性能越好。为了公平比较，我们在第一个实验中使用了相同的 HDR 数据集，并计算了三个平均质量分数（结构保真度、统计自然度和整体质量）及其标准偏差。结果列于表II。尽管 Mantiuk 的方法 [5] 在结构保真度方面比提出的对比度增强色调映射方法略好，但在统计自然度和整体性能方面，提出的方法优于 Mantiuk 的方法。此外，表 II 中的标准差表明，所提出的对比度增强方法的每个质量得分往往接近平均质量得分。

使用所提出的对比度增强方法的色调映射结果获得了各种 HDR 图像的高分。请注意，这种趋势在图 1 和图 2 中清晰可见。如图 7 和 8 所示，与其他色调映射方法相比，所提出的对比度增强方法的色调映射 LDR 图像不仅保留了局部细节，而且显示出更好的视觉质量。

5. Conclusion

在本文中，我们介绍了一种新的基于人类视觉系统的不对称 S 型曲线 (ASC)，其中视网膜响应曲线具有不对称的形状。然后，我们提出了两个使用 ASC 的全局色调映射算子。第一个采用区域系统根据 HDR 图像确定映射曲线的曲率。第二个是通过使用 HDR 图像的亮度直方图制定双准则优化问题来增强色调映射 LDR 图像的全局对比度。由于可以以封闭形式计算该问题的最优解，因此它需要较低的计算复杂度。所提出的色调映射算子使用两种定量质量评估方法进行了评估，并显示出与先前方法相比的高性能。

Acknowledgements

这项工作得到了韩国政府 (MSIT) (2017-0-00250, Intelligent Defense Boundary Surveillance Technology Using Collaborative Reinforced Learning of Embedded Edge Camera and Image Analysis) 资助的信息和通信技术促进研究所 (IITP) 赠款的支持