数据结构----结构--线性结构--链式存储--链表
数据结构----结构–线性结构–链式存储–链表
1.链表的特点
空间可以不连续,长度不固定,相对于数组灵活自由
搜索:
时间复杂度O(n)
增删:
头增头删时间复杂度O(1)
其他时间复杂度为O(n)
扩展:单向循环链表的特性
从任意节点出发皆可遍历整个链表
2.链表的组成
链表由数据域和指针域组成
3.链表及其功能的实现
1.创建一个链表,并查看每一个链表中所存的值
//在Visual Studio 2022编译器下的用c语言的写法
#include 思考如何将链表反向打印,不破环原有链表结构
方法:
1.暴力 时间复杂度O(n的平方) 空间复杂度O(1)
2.交换 时间复杂度O(n的平方) 空间复杂度O(看怎么使用交换来确定)
3.栈 时间复杂度O(n) 空间复杂度O(n)
4.头插法造新链表 时间复杂度O(n) 空间复杂度O(n)
5.数组 时间复杂度O(n) 空间复杂度O(n)
6.递归 时间复杂度O(n) 空间复杂度O(n)
这里用递归进行实现
//此函数的定义及其实现依赖于上面的链表代码
void ReserveList(List* head) {
if (head->pNext == NULL) {//如果到了最后一个节点
printf("%d ", head->nValue);//打印该节点
return;//返回
}
ReserveList(head->pNext);//先处理下一个
printf("%d ", head->nValue);//打印当前节点
}
2.将链表进行反转(用不消耗空间的方法)
消耗空间的方法:
1.栈
2.数组
3.递归
4.头插法创建一个新链表
不消耗空间的方法
用三个指针来实现
1.分别记三个指针为头,拿,断
2.处理:(1)插入 :将拿的指针所指的节点的下一个节点改为头指针所指向的节点
(2)改变标记:头的指针所指向的节点变为拿的指针所指向的节点
拿的指针所指向的节点变为断的指针所指向的节点
断的指针所指向的节点为断的指针所指向的节点的下一个节点
代码实现
//此函数的定义及其实现依赖于上面的链表代码
List* FanZhuan(List* P_head) {
if (P_head == NULL || P_head->pNext == NULL) return P_head;
List* NewHead = NULL;
List* Na = P_head;
List* Duan = P_head->pNext;
while (Duan) {
Na->pNext = NewHead;
NewHead = Na;
Na = Duan;
Duan = Duan->pNext;
}
Na->pNext = NewHead;
return Na;
}
3.将两个链表进行合并且按照链表中数据的大小进行排序
方法:
1.定义两个指针一个确定新表头之后指向新表头(后续会对这个指针进行操作),一个指向新表头之后进行返回
2.处理:用传入的两个指针比较两链表,之后在新链表进行尾添加,然后相应的指针移到下一个节点,直到两个指针中的其中一个指针指向为空结束循环
3.将有剩余链表与新链表的尾部进行连接
代码实现
//此函数的定义及其实现依赖于上面的链表代码
List* HeBing(List* list1_head, List* list2_head) {
if (!list1_head) {
return list2_head;
}
if (!list2_head) {
return list1_head;
}
List* newHead = NULL;
List* HEAD = NULL;
if (list1_head->nValue < list2_head->nValue) {//确定表头
newHead = list1_head;
HEAD = newHead;
list1_head=list1_head->pNext;
}
else {
newHead = list2_head;
HEAD = newHead;
list2_head = list2_head->pNext;
}
while (list1_head && list2_head) {//循环判断拼接链表
if (list1_head->nValue < list2_head->nValue) {
newHead->pNext = list1_head;
newHead = newHead->pNext;
list1_head = list1_head->pNext;
}
else {
newHead->pNext = list2_head;
newHead = newHead->pNext;
list2_head = list2_head->pNext;
}
}
if (list1_head) {
newHead->pNext = list1_head;
}
if (list2_head) {
newHead->pNext = list2_head;
}
return HEAD;
}
4.链表题目的练习
第一题(网址为https://leetcode.cn/problems/LGjMqU/)
题目:
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln-1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
解决:
方法一:
暴力(不用这个)
方法二:
第一步:将这个链表从中间拆成两个链表(如果不是偶数长度,则前一个链表比后一个长一个节点)
第二步:翻转第二个链表
第三步:将两个链表进行合并,合并的方法为先第一个链表的节点,再第二个链表的节点,以此类推
代码如下
//这里的代码是c++语言下的
class Solution {
public:
void reorderList(ListNode* head) {
if(head->next==nullptr) return;
int listsize=0;
ListNode* headsize=head;
while(headsize){//判断链表长度
listsize++;
headsize=headsize->next;
}
if(listsize==2){//如果链表长度为2,结束
return;
}
headsize=nullptr;
//将链表分成两个
int listsize2=listsize/2; //链表2长度
int listsize1=listsize-listsize2;//链表1长度
ListNode* Temp=nullptr;
ListNode* head1=head;//链表一头节点
ListNode* head2=head;//链表二
if(listsize1==1){//将链表一与链表二断开 1
Temp=head1;
}
while(listsize1--){//遍历获得链表二头节点
head2=head2->next;
if(listsize1==1){
Temp=head2;//记录链表一的尾节点
}
}
Temp->next=nullptr;//将链表一与链表二断开 2
Temp=nullptr;
ListNode* Temp1=nullptr;
ListNode* Temp2=nullptr;
//将链表二进行翻转
//链表长度大于1进行翻转
if(listsize2>1){
ListNode*NewlistHead=nullptr;
ListNode*Na=head2;
ListNode*Duan=head2->next;
while(Duan){
Na->next=NewlistHead;
NewlistHead=Na;
Na=Duan;
Duan=Duan->next;
}
Na->next=NewlistHead;
//将两链表进行拼接 第一种
Temp1=head1;
Temp2=Na;
}
else{//不大于1
//将两链表进行拼接 第二种
Temp1=head1;
Temp2=head2;
}
while(1){
ListNode* Temp3=Temp1->next;
Temp1->next=Temp2;
Temp1=Temp3;
if(Temp2==nullptr||Temp1==nullptr){
break;
}
ListNode* Temp4=Temp2->next;
Temp2->next=Temp1;
Temp2=Temp4;
}
}
};
第二题(网址为https://leetcode.cn/problems/3u1WK4/)
题目:
给定两个单链表的头节点 headA 和 headB ,请找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
解决:
方法一:
暴力(不用这个 用的时间和空间太多了)
方法二:
栈 (两个链表出栈时,进行比较,看是否有相同的)
方法三:
差值法:
第一步:遍历两个链表获得两个链表的长度
第二步:进行相减,获得长度差
第三步:长的那个先走长度差的距离,之后两个指向链表的指针一起走,
如果两个指针指向相同的节点时,结束找到了。
如果两个链表指向空地址了还没找到,结束没找到。
这里用方法三来写,方法三的代码如下
//这里的代码是c++语言下的
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int headAsize=0;
int headBsize=0;
ListNode*headA1=headA;
ListNode*headB1=headB;
int x=0;
while(headA1){
headAsize++;
headA1=headA1->next;
}
while(headB1){
headBsize++;
headB1=headB1->next;
}
headA1=headA;
headB1=headB;
if(headAsize>=headBsize){
x=headAsize-headBsize;
while(x--){
headA1=headA1->next;
}
}
else{
x=headBsize-headAsize;
while(x--){
headB1=headB1->next;
}
}
while(1){
if(headA1==headB1) return headA1;
if(headA1==nullptr||headB1==nullptr) return 0;
headA1=headA1->next;
headB1=headB1->next;
}
}
};
第三题(网址为https://leetcode.cn/problems/c32eOV/)
题目:
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
**说明:**不允许修改给定的链表。
解决:
方法一
快慢指针:
第一步:用快慢指针找到交点(如果找不到节点就是无环)
第二步:将交点断开(之后要还原)
第三步:定义从交点和起始点开始的两个指针,遍历获得长度
第四步:进行相减,获得长度差
第五步:长的那个先走长度差的距离,之后两个指向链表的指针一起走,
两个指针指向相同的节点时,返回该节点。
方法二:
将链表进行翻转,将链表每一次要翻转的链表进行一个存储(用指针数组存),之后在存储的这个指针数组中,数组的头和尾一起往中间遍历,当第一次找到不一样的节点时,返回上一次的节点就是入环点
方法三:
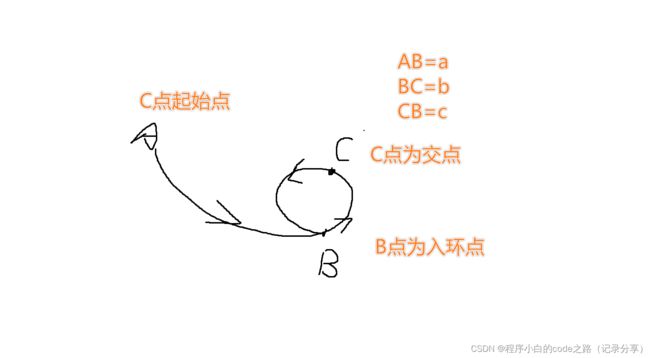
数学推导法:
经过推导得 a=(R-1)(b+c)+c
所以得出只要用两个指针指向A点和C点并且同时同速度出发,最后就会在B点相遇,可得入环点
这里用方法一来写,方法一的代码如下
//这里的代码是c++语言下的
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
if(head==nullptr){//如果没节点返回空,无环
return head;
}
if(head->next==nullptr){//如果只有一个节点返回空,无环
return 0;
}
//定义快慢指针
ListNode *Fast=head;
ListNode *Slow=head;
//定义一个指针指向交点
ListNode *JiaoDian=nullptr;
ListNode *JiaoDian2=nullptr;
//快慢指针进行遍历找到交点
while(1){
if(Fast->next==nullptr){//如果快指针会指向为空,无环
return Fast->next;
}
else if(Fast->next->next==nullptr){
return Fast->next->next;
}
Fast=Fast->next->next;
Slow=Slow->next;
if(Fast==Slow){//找到交点
JiaoDian=Fast;
JiaoDian2=Slow=Slow->next;//断点的下一个
Fast->next=nullptr;//将交点断开,一会要还原
break;
}
}
//定义从交点和起始点开始的指针
ListNode *StartJiao=Slow;
ListNode *Start=head;
//遍历两个指针获得长度
int StartJiaolen=0;
int Startlen=0;
while(StartJiao){//起点开始的长度
StartJiaolen++;
StartJiao=StartJiao->next;
}
while(Start){//断点开始的长度
Startlen++;
Start=Start->next;
}
StartJiao=Slow;//回到起点
Start=head;
int chalen=0;//相差长度
if(StartJiaolen>Startlen){
chalen=StartJiaolen-Startlen;
while(chalen--){//移动交点指针
StartJiao=StartJiao->next;
}
}
else{
chalen=Startlen-StartJiaolen;
while(chalen--){//移动开始指针
Start=Start->next;
}
}
while(1){//移动找到入口点
if(Start==StartJiao){
JiaoDian->next=JiaoDian2;
return Start;
}
if(Start->next==nullptr||StartJiao->next==nullptr){
return 0;
}
Start=Start->next;
StartJiao=StartJiao->next;
}
}
};
第四题(网址为https://leetcode.cn/problems/fu-za-lian-biao-de-fu-zhi-lcof/)
题目:
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
解决:
方法一:
暴力 时间复杂度为O(n的平方) ,时间太久,不用此方法
方法二:
第一步:创建一个新链表(实现了next指针)
第二步:将两个链表交叉合并
第三步:实现(random指针)
第四步:将两个链表分开还原
第五步:返回新链表
时间复杂度为O(n) 空间复杂度为O(1)
代码如下
//这里的代码是c++语言下的
class Solution {
public:
Node* copyRandomList(Node* head) {
if(head==nullptr){
return head;
}
Node* BianLi=head;//用于遍历原来链表的指针
Node* NewHead=nullptr;//新链表
Node* Temp=nullptr;//用来指向新链表的表头
//添加完成新链表(random指针还没有实现)
NewHead=Temp=NewNode(*BianLi);//表头
BianLi=BianLi->next;
while(BianLi){
Node* Temp2=NewNode(*BianLi);
BianLi=BianLi->next;
Temp->next=Temp2;
Temp=Temp->next;
}
//将两个链表相交连接
Temp=NewHead;//重置 用于遍历新链表的指针
BianLi=head;//重置 用于遍历原来链表的指针
while(1){
Node* LinShi1=BianLi->next;//临时变量
BianLi->next=Temp;
BianLi=LinShi1;
if(BianLi==nullptr){
break;
}
Node* LinShi2=Temp->next;//临时变量
Temp->next=BianLi;
Temp= LinShi2;
}
//将random指针实现
Node* Temp3=head;//用于遍历合并后两个链表的指针
int bool1=1;//判断是不是原有链表的节点
while(1){//循环将复制的节点的复杂指针实现
if(bool1%2==1){
if(Temp3==nullptr){//结束条件
break;
}
if(Temp3->random==nullptr){//如果指向为空,那对应的就给空,这里是因为我合并的那个链表只有一个nullptr
Temp3->next->random=nullptr;
}
else{
Temp3->next->random=Temp3->random->next;
}
}
Temp3=Temp3->next;
bool1+=1;
}
//将两个链表进行拆分
Temp3=head;//重置 用于遍历合并后两个链表的指针
while(1){
if(Temp3==nullptr){//终止条件
break;
}
Node* LinShi1=Temp3->next;//临时变量
if(Temp3->next==nullptr||Temp3->next->next==nullptr){//最后两个数据的处理
Temp3->next=nullptr;
}
else{
Temp3->next=Temp3->next->next;
}
Temp3=LinShi1;
}
return NewHead;
}
//造新节点
Node* NewNode(Node node){
Node*newnode=(Node*)malloc(sizeof(Node));
newnode->val=node.val;
newnode->next=nullptr;
newnode->random=nullptr;
return newnode;
}
};
5.如何判断一个数字是不是2的整数次幂(此题与链表无关)
整数为n 用n&(n-1)看是否等于0等于0就是2的整数次幂
6.找到一个数二进制是1的一位(随机的找是1的一位)(此题与链表无关)
整数为n 用n&(-n)就可以找到了
7.跳跃列表:SkipList(并不是一个链表结构)
跳跃列表基于有序链表
1.跳表查找的实现
1.根据链表的长度判断有几层 层数=log2的链表长度
2.每一层有哪些元素是根据概率来定的(每一个元素是否有的概率都是二分之一)
3.然后找数是从高层往低层找 在每一层跟链表中的元素做比较大于就取右边,小于就取左边,等于就是找到了(这一步和二分类似)
4.到最后一层看是否找到
2.跳表添加的实现
1.根据链表的长度判断有几层 层数=log2的链表长度
2.每一层有哪些元素是根据概率来定的(每一个元素是否有的概率都是二分之一)
3.然后从高层往低层 依次找到要添加的元素在每层该插入的地方,并存起来
4.根据概率判断每一层是否都有这个元素(概率是二分之一)
5.进行插入
8.哈希表(散列表):hashTable
1.确定分组
用求整取余法 公式为:P=key%M(M是个数) (会产生哈希冲突问题)
2.定哈希冲突解决方案
1.开放定址法:
1.线性探测
2.二次探测
2.拉链法:
第一步:定义一个链表结构体
第二步:申请指针数组(数组中每个元素初值为空)
第三步:元素入组(头插法)
第四步:查找
用拉链法实现简单哈希表代码如下(此代码是用c语言写的)
#include 3.线性探测的优化
装载因子 α=元素/表长 <0.8 越趋近于0.8冲突的可能性越高
优化的方法就是申请的空间大些尽量让装载因子小于0.8
4.拉链法与线性探测优化各自的优势
拉链法:
1.处理冲突简单
2.删除数据容易
3.适用于未知元素个数的情况
4.处理元素所占空间大且多的情况,用的空间少
线性探测优化:
处理元素所占空间小且少的情况,用的空间少