数羊

H题数羊

第八届“图灵杯”NEUQ-ACM程序设计竞赛个人赛

题目描述

憨憨小杨晚上睡不着觉，就开始数羊，她觉得一只一只数太慢了，突发奇想出了一种新的数羊方式，羊羊数量A(n,m)由两个整形变量n和m决定，计算方式如下:

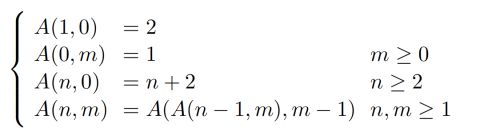
现在给出n和m的值，请你帮小杨数数一共有多少只羊。

输入描述:

多组输入。第一行包含一个整数T(1≤T≤1000)，表示有T组测试数据。每组测试数据包含一行，包含两个整数n(1≤n≤10^9)和m(0≤m≤2).

输出描述:

对每一组输入，在一行中输出A(n,m)的值,由于输出的结果可能会很大，答案对998244353取模

示例1

输入

3
3 0
3 1
3 2

输出

5
6
8

当初看到这题的时候，这不就是一个分段函数吗，只是用到了递归，可当我写完之后并提交，发现爆内存了。

原来，像这种 阿克曼函数 ，最后一个函数递归太多次，把栈递归穿了，那该怎么办呢？

有没有发现，题目的数据范围中，0≤m≤2，所以m只能是0，1，2。所以我们可以分类讨论。

1.当m==0的时候，上面已经有对应的表达式了。

2.当m == 1的时候，则A(n,1)=A(A(n-1,1),0),这时就可以套用第三个函数，也就是说，A(n,1)=A(n-1,1)+2。左边的n一直减小，直到n==0，就到了第二个式子，等于1，这里面加了n-1个2和最后一个1，所以，A(n,1)=2*(n-1)+1吗？其实不是的。

我们观察最后一个函数，发现里面有个n-1，也就是说当n == 1的时候A(1,m)=A(A(0,m),m-1),由第二个式子A(0,m)=1得，A(1,m)=A(1,m-1)，m一直减小，直到m==0，此时符合第一个式子，等于2，因此我们得出一个结论：
$$A(1,m)=2$$

回到刚才，当n减小到1的时候就停在了2，所以实际上有n个2相加，所以
$$A(n,1)=2\ast n$$

3.当m==2的时候，也用同样的分析方法，A(n,2)=A(A(n-1,2),1),此时套用上面的结论A(n,1)=2*n，得出A(n,2)=A(A(n-1,2),1)=2A(n-1,2)，当n减小到1时符合第一个式子，有n个2相乘，因此
$$A(n,2)=pow(2,n)$$

这样就根据m的取值，进行了分类讨论，将看似是阿克曼函数的问题转化成了单纯用if语句就能做的问题

#include
#include
#include
#include
#include
#define endl '\n'
#define int long long
#define Please return
#define AC 0
using namespace std;
const int N=1e5+7;
void fastio(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);}
int qpow(int a,int b,int m){int ans=1;while(b){if(b&1)ans=ans*a%m;b>>=1;a=a*a%m;}return ans;}

int func(int a,int b)
{
  if(b==0)
​    return (a+2)%998244353;
  else if(b==1)
​    return (2*a)%998244353;
  else
​    return qpow(2,a,998244353);//快速幂
}

signed main()
{
  fastio();
  int t;
  cin>>t;
  while(t--)
  {
​    int a,b;
​    cin>>a>>b;
​    cout<<func(a,b)<<endl;
  }
  Please AC;
}