玩转带头双向链表——【数据结构】
W...Y的主页
今天我们接着来说数据结构——带头双向链表
目录
带头双向链表的实现
结构体的创建
初始化兵创建哨兵节点
释放链表所以内容
打印链表函数
尾插
尾删
头插
编辑
头删
计数函数实现
查找数据相应位置函数
在pos位置之前插入
在pos位置删除
顺序表与链表的差别
带头双向链表(Doubly Linked List with Head)相对于普通的双向链表,添加了一个头节点(head node),头节点不存储任何实际的数据,仅用于指示链表的起始位置。下面是带头双向链表的一些优点:
链表操作方便:带头双向链表提供了直接访问链表头部和尾部的能力,使得链表的插入、删除等操作更加高效。你可以通过头节点快速插入第一个元素,也可以通过尾节点快速插入新元素。同时,由于链表的双向性,你可以轻松地在链表中的任意位置进行插入和删除操作。
遍历灵活性:带头双向链表可以从头到尾或从尾到头两个方向遍历。这意味着你可以根据需要选择合适的遍历方式,无论是从前向后还是从后向前遍历链表,都能方便地获取元素。
反向查找:带头双向链表的一个重要优点是可以通过后向链接(back link)从任意节点快速访问该节点的前一个节点。这使得在链表中进行反向查找变得高效。与单链表相比,带头双向链表的反向查找时间复杂度从O(n)降至O(1),这对某些应用程序可能非常重要。
方便的删除节点:在带头双向链表中,删除一个节点不需要访问其前一个节点,只需修改当前节点的前后链接即可。这样,节点的删除操作变得更为方便和高效。
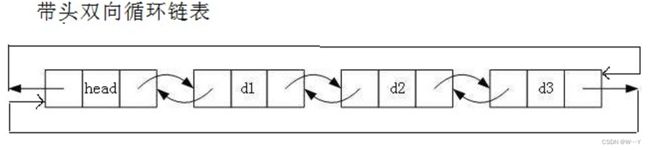
带头双向循环链表:结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构,都是带头双向循环链表。另外这个结构虽然结构复杂,但是使用代码实现以后会发现结构会带 来很多优势,实现反而简单了,后面我们代码实现了就知道了。
带头双向链表的实现
结构体的创建
typedef int LTDataType;
typedef struct ListNode
{
int data;
struct ListNode* next;
struct ListNode* prev;
}LTNode;创建结构体使用typedef将其改名LTNode方便使用,创建next和prev节点用来保存下一个节点与上一个节点。
初始化兵创建哨兵节点
我们创建哨兵位时,可以在data中间增加-1,创建好后将next与prev全部指向自己。但是这个功能与怎加节点函数内容及其相似,所以我们可以先创建节点函数,然后再初始化哨兵位时将其调用即可,防止冗余现象。
LTNode* BuyLTNode(LTDataType x)
{
LTNode* node = (LTNode*)malloc(sizeof(LTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->data = x;
node->prev = NULL;
return node;
}LTNode* LTInit()
{
LTNode* phead = BuyLTNode(-1);
phead->next = phead;
phead->prev = phead;
return phead;
}我们再创建好两个函数时,让LTInit函数去调用BuyLTNode函数,将哨兵位初始化即可。
释放链表所以内容
因为链表使用realloc开辟的空间全部在堆区,所以必须将链表开辟的空间全部释放,防止内存泄漏。
void LTDestory(LTNode* phead)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
LTNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
phead = NULL;
}打印链表函数
在打印链表时,我们要将次链表与单链表区分。单链表只需找到尾NULL即可停止,而双向链表的尾部指向哨兵位,所以我们可以换一种方法进行检测。
void LTPrint(LTNode* phead)
{
assert(phead);
LTNode* cur = phead->next;
printf("phead<->");
while (cur != phead)
{
printf("%d<->", cur->data);
cur = cur->next;
}
}我们创建一个遍历指针cur,让cur = phead->next指向哨兵位下一个节点。然后进行遍历,如果遍历返回到哨兵位phead停止即可。
尾插
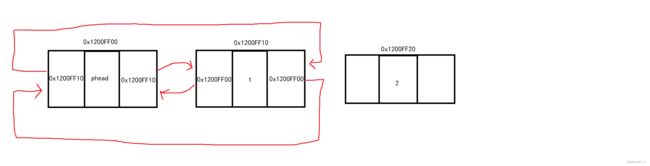
尾插相对于单链表也非常方便,不用遍历找尾节点,只需要访问phead的prev即可找到尾节点。
void LTPushBack(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* tail = phead->prev;
LTNode* newnode = BuyLTNode(x);
newnode->prev = tail;
newnode->next = phead;
tail->next = newnode;
phead->prev = newnode;
}尾删
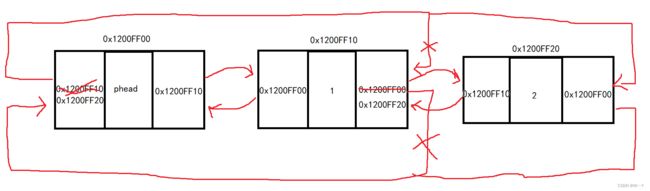
我们首先得检测phead哨兵位是否为空,如果链表为空我们也不能正常进行删除,所以我们得继续判断phead->next != phead。自己的下一个节点不能指向自己。
void LTPopBack(LTNode* phead)
{
assert(phead);
assert(phead->next != phead);
LTNode* tail = phead->prev;
phead->prev = tail->prev;
tail->prev->next = phead;
free(tail);
}删除就非常简单,访问最后一个节点记作tail,将phead连接尾节点的地址切换成尾节点的上一个节点,然后将尾节点上一个节点的next换成哨兵位地址,free掉tail尾节点即可。
头插
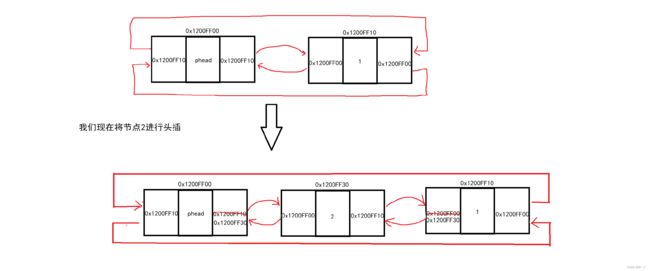
头插与尾插原理基本相同,只需要将哨兵位的内容进行改变即可。
void LTPushFront(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* newnode = BuyLTNode(x);
/*newnode->next = phead->next;
phead->next->prev = newhead;
phead->next = newhead;
newhead->prev = phead;*/
LTNode* first = phead->next;
phead->next = newnode;
newnode->prev = phead;
first->prev = newnode;
newnode->next = first;
}我们可以参照上述代码进行头插,分别有两种方法。第一种(已注释)是不创建任何指针变量进行交换替代,第二种(未注释)即创建变量进行交换。第一种方法再交换次序上必须严谨,先进行尾节点的交互,再进行首节点的交互,否则会交换失败出现错误数据。
头删
在删除时,务必检测链表是否为空,链表是否只有哨兵位方可进行删除操作。
void LTPopFront(LTNode* phead)
{
assert(phead);
assert(phead->next != phead);
LTNode* first = phead->next;
LTNode* second = first->next;
free(first);
phead->next = second;
second->prev = phead;
}
计数函数实现
当我们录入数据量过大时,为了方便计数所创建的函数。‘
int LTsize(LTNode* phead)
{
assert(phead);
int size = 0;
LTNode* cur = phead->next;
while (cur != phead)
{
++size;
cur = cur->next;
}
return size;
}这里只需遍历链表种的每一个节点直到返回到哨兵位即可。
查找数据相应位置函数
当操作人员想知道某个数据在链表中的位置并进行操作时,我们即可调用此函数来返回相应数据所在节点的地址。
LTNode* LTFind(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* cur = phead->next;
while(cur != phead)
{
if (cur->data == x)
return cur;
}
return NULL;
}这里我们使用暴力查找的算法进行整组链表搜索,找到对应数据即可返回。
在pos位置之前插入
这里我们就需要与查找位置函数进行联动配合进行调用。
void LTInsert(LTNode* pos, LTDataType x)
{
assert(pos);
LTNode* posprev = pos->prev;
LTNode* newnode = BuyLTNode(x);
posprev->next = newnode;
newnode->next = pos;
newnode->prev = posprev;
pos->prev = newnode;
}这里其实与头插尾插原理一样,所以我们也可以用此函数进行头插尾插,只需将pos参数传入正确,分别为phead->next(头插)、phead->prev(尾插)。
在pos位置删除
void LTErase(LTNode* pos)
{
assert(pos);
LTNode* posprev = pos->prev;
LTNode* posnext = pos->next;
free(pos);
posprev->next = posnext;
posnext->prev = posprev;
}这里也是与头删尾删原理相同,只需将参数传入正确即可变成头删和尾删。
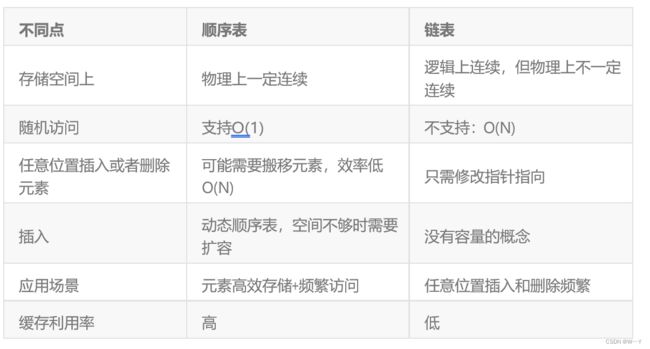
顺序表与链表的差别
所以在不同情况下选择不同的数据结构时是很关键的,我们需要足够了解其中的差别与优势,才能满足各种问题下不同的需求。