华为OD机试真题 Java 实现【跳格子游戏】【2023 B卷 200分】，附详细解题思路

华为OD机试 2023B卷题库疯狂收录中，刷题点这里

专栏导读

本专栏收录于《华为OD机试（JAVA）真题（A卷+B卷）》。

刷的越多，抽中的概率越大，每一题都有详细的答题思路、详细的代码注释、样例测试，发现新题目，随时更新，全天CSDN在线答疑。

一、题目描述

地上共有N个格子，你需要调完地上所有的格子，但是格子间是有强依赖关系的，跳完前一个格子后，后续的格子才会被开启，格子间的依赖关系由多组steps数组给出，steps[0]表示前一个格子，step[1]表示steps[0]可以开启的格子。

比如[0,1]表示从跳完第0个格子以后第1个格子就开启了，比如[2,1],[2,3]表示跳完第2个格子后第1个格子和第3个格子就被开启了。

请你计算是否能由给出的steps数组跳完所有的格子，如果可以输出yes，否则输出no。

说明：

• 你可以从一个格子调到任意一个开启的格子；
• 没有前置依赖条件默认就是开启的；
• 如果总数是N，则所有的格子编号为[0,1,2,3…N-1]l连续的数组

二、输入描述

第一行输入两个正整数，第一个整数N表示总共有多少个格子，第二个整数表示二维数组的大小M。

接下来的M行输入二维数组steps表示所有格子之间的依赖关系。

三、输出描述

如果能按照steps给定的依赖顺序跳完所有的格子输出yes，否则输出no。

四、解题思路

深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索，最糟糕的情况算法时间复杂度为O(n)。

1. 输入N个格子，二维数组的大小M，通过java8 Stream表达式（简洁/方便/上档次）快速拆解输入行；
2. 初始化边edgeLists；
3. 遍历所有节点；
4. 如果节点未被遍历，从该节点开始遍历；
   • 标记节点为正在遍历；
   • 遍历邻居节点；
     • 如果邻居节点未被遍历，递归遍历邻居节点，如果已经无法跳完所有格子，直接返回；
     • 如果邻居节点已被遍历但未完成遍历（即在当前遍历路径中），无法跳完所有格子，标志置为false；
   • 标记节点为遍历完成；
5. 输出结果；

五、Java算法源码

package com.guor.od;

import java.util.*;

public class OdTest {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int[] line1 = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
        // 输入N个格子
        int N = line1[0];
        // 二维数组的大小M
        int M = line1[1];

        // 初始化边
        List<List<Integer>> edgeLists = new ArrayList<>();
        for(int i = 0; i < N; i++) {
            edgeLists.add(new ArrayList<>());
        }
        List<statusEnum> statusList = new ArrayList<>(Collections.nCopies(N, statusEnum.UNVISITED));

        boolean[] stepArr = { true };

        for(int i = 0; i < M; i++) {
            int[] line2 = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
            int a = line2[0];
            int b = line2[1];
            // 记录边
            edgeLists.get(b).add(a);
        }

        // 遍历所有节点
        for(int i = 0; i < N && stepArr[0]; i++) {
            // 如果节点未被遍历
            if(statusList.get(i) == statusEnum.UNVISITED) {
                // 从该节点开始遍历
                dfs(i, statusList, edgeLists, stepArr);
            }
        }

        // 输出结果
        System.out.println(stepArr[0] ? "yes" : "no");
    }

    // 格子状态
    enum statusEnum { UNVISITED, VISITING, VISITED };

    /**
     * 深度优先搜索
     * @param node
     * @param statusList
     * @param edgeLists
     * @param stepAllGrids
     */
    public static void dfs(int node, List<statusEnum> statusList, List<List<Integer>> edgeLists, boolean[] stepAllGrids) {
        // 标记节点为正在遍历
        statusList.set(node, statusEnum.VISITING);

        // 遍历邻居节点
        for(int neighbor : edgeLists.get(node)) {
            // 如果邻居节点未被遍历
            if(statusList.get(neighbor) == statusEnum.UNVISITED) {
                // 递归遍历邻居节点
                dfs(neighbor, statusList, edgeLists, stepAllGrids);

                // 如果已经无法跳完所有格子，直接返回
                if(!stepAllGrids[0]) {
                    return;
                }
                // 如果邻居节点已被遍历但未完成遍历（即在当前遍历路径中）
            } else if(statusList.get(neighbor) == statusEnum.VISITING) {
                // 无法跳完所有格子，标志置为false
                stepAllGrids[0] = false;
                return;
            }
        }

        // 标记节点为遍历完成
        statusList.set(node, statusEnum.VISITED);
    }
}

六、效果展示

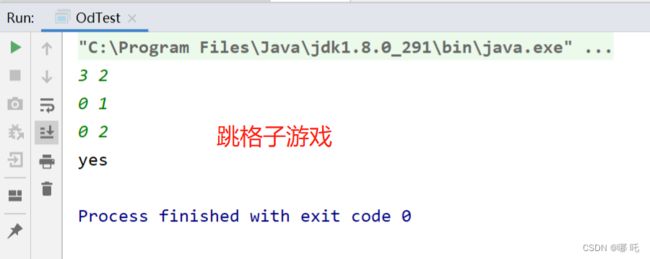
1、输入

3
0 1
0 2

2、输出

yes

3、说明

总共有三个格子[0,1,2],跳完0个格子后第一个格子就开启了，跳到第0个格子后第2个格子也被开启了，按照0->2->1 的顺序都可以跳完所有的格子。

下一篇：华为OD机试真题 Java 实现【路灯照明问题】【2022Q4 100分】，感谢fly晨发现这个问题，并提供更优质的算法

本文收录于，华为OD机试（JAVA）真题（A卷+B卷）

刷的越多，抽中的概率越大，每一题都有详细的答题思路、详细的代码注释、样例测试，发现新题目，随时更新，全天CSDN在线答疑。