简单记录牛客top101算法题（初级题C语言实现）BM17 二分查找 && BM21 旋转数组的最小数字 && BM23 二叉树的前序遍历

1. BM17 二分查找

   要求：给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标（下标从 0 开始），否则返回 -1。

输入：[-1,0,3,4,6,10,13,14],13
返回值：6
说明：13     出现在nums中并且下标为6   

1.1 自己的整体思路

1. 使用二分法，先定义三个指针，左指针，右指针，中间指针。
2. 比较中间指针对应数值与目标数值是否相等，如果相等直接返回该点索引；如果目标值大于中间值，则移动左指针，另其为中间指针加上1；如果目标值小于中间值，则移动右指针，另其为中间指针减1。
3. 直到左指针大于右指针，结束整个循环，这时是没有找到与目标值对应的索引的。

#include 
#include 
int search(int* nums, int numsLen, int target ) {
    // write code here
    int n_pre = 0;                           //首指针位置
    int n_next = numsLen - 1;                //尾部指针位置
    int n_mid = (n_pre + n_next) / 2;        //中间指针位置
    if (numsLen == 0) {                      //数组为空的情况
         return -1;
    }
    while ( nums[n_mid] != target ) {        //中间值是否等于目标值
        if ( nums[n_mid] < target) {         //目标值在中间右侧
           n_pre = n_mid + 1;                //更新左索引
           n_mid = (n_pre + n_next)/2;       //更新中间索引
        }else {
            n_next = n_mid - 1;                //更新右索引
            n_mid = (n_pre + n_next)/2;       //更新中间索引
        }
       if ( n_pre > n_next ) {                //左指针大于右指针,结束整个循环
        return -1;
    }
  }
    return n_mid;
}

  开始上面的结束条件写成了这样的了：

    if ( n_pre == n_next ) {                  //没有找到，最终两个索引会重合   会出现在右边的情况，不是一直到最后都会重合的
            if (nums[n_pre ] == target) {
                  return n_pre ;
            }else {
                  return -1;
        }
      }

  认为两个指针一定会重合，只要判断重合时候的情况就能结束整个循环,但是未通过所有的测试。

1.2 其他的方法（标准判断方法）

  判断条件是左索引是否大于右索引。

int search(int* nums, int numsLen, int target ) {
    // write code here
    if(numsLen == 0) return -1;
    int left=0, right=numsLen-1;
    while(left<=right) {
        int mid = left+(right-left)/2;
        if(nums[mid]==target) return mid;
        if(nums[mid]<target) left=mid+1;
        if(nums[mid]>target) right=mid-1;
    }
    return -1;
}

2. BM21 旋转数组的最小数字

   要求：有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，即把一个数组最开始的若干个元素搬到数组的末尾，变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。请问，给定这样一个旋转数组，求数组中的最小值。

输入：[3,4,5,1,2]
返回值：1

  这个题开始使用的分类讨论的情况，情况太多了，最后也没有写出来，下面是参考大佬的写法：
核心思想：

1.计算中间位置 mid，并与 right 指针所指向的元素进行比较：
 如果 rotateArray[mid] > rotateArray[right]，说明最小值在 mid 右侧，将 left 更新为 mid + 1。
 如果 rotateArray[mid] < rotateArray[right]，说明最小值在 mid 左侧或就是 mid，将 right 更新为 mid。
 如果 rotateArray[mid] == rotateArray[right]，无法确定最小值在哪一侧，但是可以排除 right 指针所指向的元素，将 right 向前移动一位，缩小搜索范围。
2. 循环继续，直到 left 和 right 指针相邻或重合。最终，right 指向的位置即为最小值所在位置。

int minNumberInRotateArray(int* rotateArray, int rotateArrayLen ) {
    int left=0, right=rotateArrayLen-1;
    while(left<right) {
        int mid = left+(right-left)/2;
        if(rotateArray[mid]>rotateArray[right]) left=mid+1;         //说明最小值在右边
        else if(rotateArray[mid]<rotateArray[right]) right=mid;     //说明最小值在左边
        else right--;    //22212或者10111                            //不能说明在左边还是右边，但是肯定不是右值，索引减去1再进行比较                        //关注右边，从右边出发
    }
    return rotateArray[right];
}

3. BM23 二叉树的前序遍历

   要求：给你二叉树的根节点 root ，返回它节点值的前序遍历。
                    

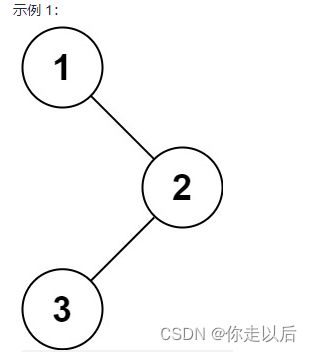
输入：{1,#,2,3}
返回值：[1,2,3]

3.1 自己的整体思路

1. 使用二叉树的前序遍历方法，递归完成二叉树元素的访问。
2. 这里访问二叉树的元素，需要传一个变量（接收数组的索引地址），因为最后结果需要返回该索引值。

具体代码如下：

#include 
#include 
#include 
#include 
void visit_root(struct TreeNode* p ,int *arr, int *a){         //访问二叉树的元素，存到数组中去
    *(arr + *a) = p->val;
    //arr[*a] = p->val;    //写成这样也是可以的
    // *a++;               //这样是错的，优先级不一样，++的优先级要高
    (*a)++;          //索引加1
   }
 void  Preorder(struct TreeNode* p , int *arr, int *a){        //遍历二叉树
         if (p != NULL) {
            visit_root(p , arr, a);
            Preorder(p->left,  arr, a);    //递归左子结点         //这行代码为空的时候，才会运行到下一行
            Preorder(p->right, arr, a );   //递归右子结点
        }
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    //前序遍历 先根，再左，再右
    struct TreeNode* cur =  root;                           //接收根结点
    int*  result = (int *)malloc(100 * sizeof(int));        //申明一个100的空数组
    int a = 0;                                              //接收数组的索引
    int *i = &a;                                            //接收a的地址
    Preorder(cur, result, i);                               //遍历二叉树 
    *returnSize = *i;                                       //必须给行号 ，卡了半天
    return result;
}

3.2 大佬的方法

1. 先判断二叉树有多少元素，这样再动态申请多大的内存。
2. 遍历二叉树即可。

int TreeSize(struct TreeNode* root)
{
   if(root==NULL)
   {
       return 0;
   }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}
void preorder(struct TreeNode* root, int* a,int *i) 
{
    if(root==NULL)
    {
        return ;
    }
    a[*i]=root->val;
    ++(*i);
    preorder(root->left,a,i);
    preorder(root->right,a,i); 
}
int* preorderTraversal(struct TreeNode* root, int* returnSize ) 
{  
    int i=0; 
    int size=TreeSize(root);
    int* a=(int*)malloc(size*sizeof(int));
    preorder(root,a,&i);
    *returnSize=size;
    return a;
}

3.3 小结

3.3.1 malloc函数

   malloc（memory allocation）函数是用于动态分配内存的标准库函数之一。它是在程序运行时从堆（heap）中申请一块指定大小的内存空间，以供程序使用。
   malloc函数的原型如下：
size：要分配的内存空间的大小，以字节为单位。通常使用sizeof运算符来计算要分配的空间大小，以确保正确性。
返回值：malloc函数返回一个void指针，指向已分配内存块的起始地址。由于返回类型是void *，您需要将这个通用指针转换为适当类型的指针，然后才能访问和操作分配的内存。

void *malloc(size_t size);

   举例分配一个包含10个int元素的数组:

 int *array = (int *)malloc(10 * sizeof(int));

注意：

1. malloc分配的内存块是未初始化的，其中的值是不确定的。您应该确保在使用之前将其初始化。
2. 在使用完分配的内存后，必须使用free函数释放它，以避免内存泄漏。
3. 在调用malloc后，应该检查返回的指针是否为NULL，以防止内存分配失败。
4. malloc函数分配的内存是在堆上，与局部变量不同，不会在函数退出后销毁，需要手动释放。

3.3.2 *和++的优先级

++操作符的优先级比*操作符更高，因此会先执行++操作，然后再执行*操作。下面的a是一个int型变量指针
*a++;       //指针会往下加1，再去该地址里面的值，地址变了
(*a)++;     //取指针a对应的变量值，把变量值加1，地址没变