python蓝桥杯

对，学习要从一而终，啥都会一点点，那是没用的，总有人在这方面比你更全面，还是择一门编程语言从一而终，我决定选择python。哈哈哈哈。

真题

最短路

def dfs(node,zz):
    global lc
    if node!=zz:
        dfs(li[node-1].z,zz)
        lc+=li[node-1].mile
    
        
        
class Rode:
    #起点和终点，路径长度
    def __init__(self,qi=0,z=0,mile=0):
        self.qi=qi
        self.z=z
        self.mile=mile
n,m=map(int,input().split())
li=list()
for i in range(m):
    a,b,c=map(int,input().split())
    add_node=Rode(a,b,c)
    li.append(add_node)
                    
lc=0
for i in range(2,n+1):
    dfs(1,i)
    print(lc)
    lc=0
 我知道这个题目还有很多没有考虑到，而且这个类的结构就适合，只有唯一情况的这种，你看就是 那个二叉树 他的左和右一定是定好的了，而这个 比如说起点是1，终点是那就很多种情况了，然后这个题目是要去最短路径，肯定要比较，而且我是用列表存的这些节点，索引的时候也有一些特殊性，但是还能得30分，我已经很开心了，我也对这个全局变量和递归又有了新的感悟。哈哈，这个还是用那个字典最好储存这种了。在配上一个矩阵来存放路径，不过我在想，字典能不能后面再放一个列表呢。

def dfs(node,zz):
    global lc
    for i in table.get(node):
        lc+=dp[node][i]
        if i!=zz:
            dfs(i,zz)
       
        
        else: 
            li.append(lc)
            lc=0
            
            

            
    

n,m=map(int,input().split())
dp=[[0 for i in range(n+1)]for j in range(n+1)]
## 万能储存器
table = {}
table1={}

for i in range(m):
    father, child,mile=map(int,input().split())
    #print(type(father))
    #print(father,child)
    if father not in table:
        table[father]=[]
    
    ##print(table)
    table.get(father).append(child)
    dp[father][child]=mile

lc=0
for i in range(2,n+1):
    li=[]
    dfs(1,i)
    print(min(li))
    
    emmm，看来是我高估了我自己，我用这种套路，也只是得了30分，不过我发现了一个更好的套路，可以解决这个问题。

横向打印二叉树

这道题是很难的，啊，但是一点点去钻研是可以的，加油吧。不断地集思广益，不断地去学习，当然会收获很多了。这个，我以前做那种树的话，用字典来存储关系，这一次，我要用类了，哈哈。

emm，没有成功，照着人家大佬的学习了一下，哎呀，太难了，不愧是大佬，啊，最终也算有了一些收获，list和set以后要加括号。
我也学习了一下类，对类有了了解，但是我会继续努力的。

## 我好像知道是什么意思了，加油
class Node:
    def __init__(self,left=0,right=0,w=0,line=0,leng=0):
        self.left=left
        self.right=right
        self.w=w
        self.line=line
        self.leng=leng
class Solution:
    def printTree(self,nums):
        #将第i个节点和树中本来就存在的cur节点进行比较
        def push(i,cur):
            if node[i].w<node[cur].w:
                if node[cur].left:
                     push(i,node[cur].left)
                else:
                    node[cur].left=i
                    
            else:
                if node[cur].right:
                     push(i,node[cur].right)
                else:
                    node[cur].right=i
            #这个数字的长度
        def wrtLeng(i):
            if i<10:
                node[i].leng=1
            elif i<100:
                node[i].leng=2
            elif i<1000:
                node[i].leng=3
            elif i<10000:
                node[i].leng=4
            else:
                node[i].leng=5
        node=list()
        newnode=Node(w=nums[0])
        node.append(newnode)
        
        for i in range(1,len(nums)):
            add_node=Node(w=nums[i])
            node.append(add_node)
            push(i,0)
        for i in range(len(nums)):
            print(node[node[i].left].w,node[node[i].right].w)

                
nums=[int(i) for i in input().split()]
Solution.printTree(Solution,nums)

货物摆放

这道题就是分解为把2021041820210418 分解为3个因数 然后全排列。
不过 依据我的猜测，想要找3个因数的情况，要先把他分解为两个因数的这种，装到一个列表里面去，
虽然我不知道是为什么。 让我在看一下别人的C版本。
哎呀 我也有点小迷，为什么我3个的那种就不行呢，问题到底出在哪里呢。算了。

a=int(2021041820210418**0.5)
ans=0
rr=set()
jj=set()
for i in range(1,a+1):
    if 2021041820210418%i==0:
        rr.add(i)
        rr.add(2021041820210418//i)
        
for i in rr:
    for j in rr:
        for k in rr:
            if 2021041820210418==i*j*k:
                
                jj.add((i,j,k))


print(len(jj))

目前我终于是去的了一些收获，就是学习之后，可以自己输出了，输入转化为输出
厉害呀
Python-turtle递归画二叉树

大臣的旅费

问题描述
很久以前，T王国空前繁荣。为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J是T国重要大臣，他巡查于各大城市之间，体察民情。所以，从一个城市马不停蹄地到另一个城市成了J最常做的事情。他有一个钱袋，用于存放往来城市间的路费。

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数），他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23。

J大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式
输入的第一行包含一个整数n，表示包括首都在内的T王国的城市数

城市从1开始依次编号，1号城市为首都。

接下来n-1行，描述T国的高速路（T国的高速路一定是n-1条）

每行三个整数Pi, Qi, Di，表示城市Pi和城市Qi之间有一条高速路，长度为Di千米。

输出格式
输出一个整数，表示大臣J最多花费的路费是多少。

样例输入1
5
1 2 2
1 3 1
2 4 5
2 5 4
样例输出1
135
输出格式
大臣J从城市4到城市5要花费135的路费。
虽然超时了，后两项不对，得了50分，虽然不是满分，但是我已经非常开心了，这一段长长的代码是我自己写下来的，哈哈，而且竟然成功了，说明我递归终于有点学明白了，递归回溯。哈哈哈。这一类型的题，我终于不再那么害怕了，哈哈。

def dfs(node,pre):
    global lu
    lu=0
    for i in table.get(node):
        if i!=pre:
            dfs(i,node)
            lu+=dp[i][node]
        
n=int(input())
dp=[[0 for i in range(n+1)]for j in range(n+1)]

table={}
for i in range(n-1):
    list=[]
    for s in input().split():
        list.append(int(s))
    if list[0] not in table:
        table[list[0]]=[]
    if list[1] not in table:
        table[list[1]]=[]
    table.get(list[0]).append(list[1])
    
    table.get(list[1]).append(list[0])
    dp[list[0]][list[1]]=dp[list[1]][list[0]]=list[2]
##储存完毕
list1=[]
#print(table)
for i in range(n):
    dfs(i+1,0)
    list1.append(lu)
a=max(list1)
ans=0
for i in range(a):
    ans+=i+1+10
print(ans)

超时了 但也得了80分

连号区间数

问题描述
小明这些天一直在思考这样一个奇怪而有趣的问题：

在1~N的某个全排列中有多少个连号区间呢？这里所说的连号区间的定义是：

如果区间[L, R] 里的所有元素（即此排列的第L个到第R个元素）递增排序后能得到一个长度为R-L+1的“连续”数列，则称这个区间连号区间。

当N很小的时候，小明可以很快地算出答案，但是当N变大的时候，问题就不是那么简单了，现在小明需要你的帮助。

输入格式
第一行是一个正整数N (1 <= N <= 50000), 表示全排列的规模。

第二行是N个不同的数字Pi(1 <= Pi <= N)， 表示这N个数字的某一全排列。

输出格式
输出一个整数，表示不同连号区间的数目。

样例输入1
4
3 2 4 1
样例输出1
7
样例输入2
5
3 4 2 5 1
样例输出2
9

k=int(input())
list=[]
def check(i,j,list):
    list1=list[i:j+1]
    ##print(list1)
    if max(list1)-min(list1)==j-i:
        return 1
##不用排序 最大值减去最小值加1为区间长度 就符合标准
ans=0
for s in input().split():
    list.append(int(s))

for i in range(k):
    for j in range(i,k):#我草我忘了写range要不直接0,和4
           
        if check(i,j,list):
            ans+=1
print(ans)
        

网络寻路

问题描述
X 国的一个网络使用若干条线路连接若干个节点。节点间的通信是双向的。某重要数据包，为了安全起见，必须恰好被转发两次到达目的地。该包可能在任意一个节点产生，我们需要知道该网络中一共有多少种不同的转发路径。

源地址和目标地址可以相同，但中间节点必须不同。

如下图所示的网络。

1 -> 2 -> 3 -> 1 是允许的

1 -> 2 -> 1 -> 2 或者 1 -> 2 -> 3 -> 2 都是非法的。

输入格式
输入数据的第一行为两个整数N M，分别表示节点个数和连接线路的条数(1<=N<=10000; 0<=M<=100000)。

接下去有M行，每行为两个整数 u 和 v，表示节点u 和 v 联通(1<=u,v<=N , u!=v)。

输入数据保证任意两点最多只有一条边连接，并且没有自己连自己的边，即不存在重边和自环。

输出格式
输出一个整数，表示满足要求的路径条数。
样例输入1
3 3
1 2
2 3
1 3
样例输出1
6
样例输入2
4 4
1 2
2 3
3 1
1 4
样例输出2
10

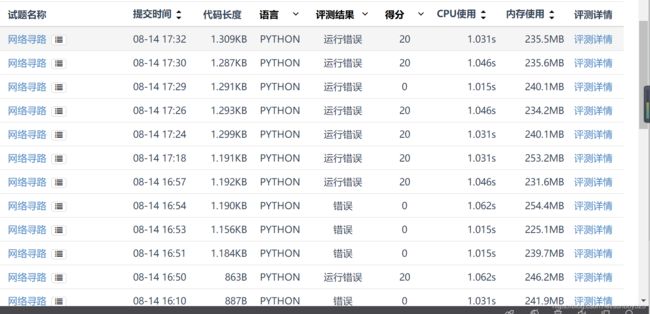
奇怪耶 不知道为啥只有20分，这是为什么呢

def dfs(node,pre,num):
    global ans
    if num==3:
        ans+=1
        return
    for i in table.get(node):
        if i!=pre:
            if dp[node][i]==0:
                 dp[node][i]=1
                 dfs(i,node,num+1)
                 dp[node][i]=0 #回溯
                
                
##            else:
##                if num==2 and i==last:
##                     ans+=1
                     
           
            

global value, table
ans=0
n,m = map(int,input().split())
##value = list(map(int, input().split()))
##value = list(map(lambda x:[0,x],value))
##father, child=list(map(int,input().split()))
    
##print(value)
##value.insert(0,0)
dp=[[0 for i in range(n+1)]for j in range(n+1)]

table = {}

for i in range(m):
    father, child=map(int,input().split())
    #print(type(father))
    #print(father,child)
    if father not in table:
        table[father]=[]
    if child not in table:
        table.update({child:[]})
    ##print(table)
    table.get(father).append(child)
    table.get(child).append(father)
    
##print(table)
#get(键值)
##for i in range(n):
##    father, child = list(map(int, input().split()))
##    table.get(father).append(child)
##    table.get(child).append(father)
##print(table)
#以上就是树的储存
for i in range(n):
    dfs(i+1,0,0)
print(ans)

哎，调了一下午也没能成功得到100，结果是有一部分运行出错，我这个用的是边的关系。他们那个啥的也不管用，算了，先就这样吧，啊。哈哈哈。通过这个 结点选择和那个网络寻路，我还是学到了很多，加油。不放弃。虽然上一个70分，这个20分，都参考了别人的代码，但我学到了很多。像今天，我就更加了解字典。而且也成功的创造出来万能储存器

万能储存器

## 万能储存器
table = {}

for i in range(m):
    father, child=map(int,input().split())
    #print(type(father))
    #print(father,child)
    if father not in table:
        table[father]=[]
    if child not in table:
        table.update({child:[]})
    ##print(table)
    table.get(father).append(child)
    table.get(child).append(father)
    

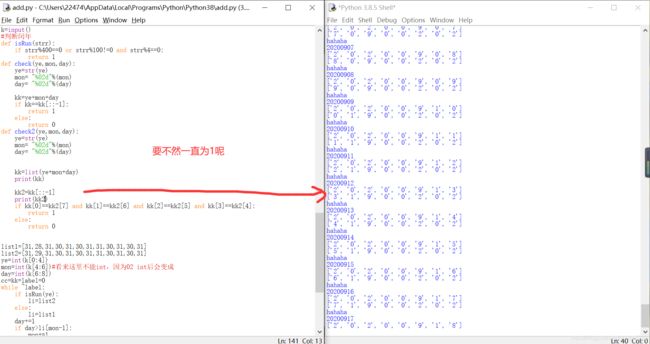
回文日期

2 但是想要输出02 保证长度

字符串拆分为字符存入列表

判断使用 取反~ 不太好

问题描述
2020年春节期间，有一个特殊的日期引起了大家的注意：2020年2月2日。因为如果将这个日期按 yyyymmdd 的格式写成一个8位数是 ，恰好是一个回文数。我们称这样的日期是回文日期。

有人表示 是“千年一遇”的特殊日子。对此小明很不认同，因为不到2年之后就是下一个回文日期： 即2021年12月2日。

也有人表示 并不仅仅是一个回文日期，还是一个 型的回文日期。对此小明也不认同，因为大约 100 年后就能遇到下一个 型的回文日期： 即2121年12月12日。算不上“千年一遇”，顶多算“千年两遇”。

给定一个8位数的日期，请你计算该日期之后下一个回文日期和下一个 型的回文日期各是哪一天。

输入格式
输入包含一个八位整数 ，表示日期。

输出格式
输出两行，每行1个八位数。
第一行表示下一个回文日期，第二行表示下一个 型的回文日期。

样例输入
20200202
Data
样例输出
20211202
21211212

k=input()
#判断闰年
def isRun(strr):
    if strr%400==0 or strr%100!=0 and strr%4==0:
        return 1
def check(ye,mon,day):
    ye=str(ye)
    mon= "%02d"%(mon)
    day= "%02d"%(day)
        
    kk=ye+mon+day
    if kk==kk[::-1]:
        return 1
    else:
        return 0
def check2(ye,mon,day):
    ye=str(ye)
    mon= "%02d"%(mon)
    day= "%02d"%(day)
    
        
    kk=list(ye+mon+day)

   
    
    if kk[0]==kk[2]==kk[5]==kk[7] and kk[1]==kk[6]==kk[3]==kk[4] :
        return 1
    else:
        return 0
    
    
list1=[31,28,31,30,31,30,31,31,30,31,30,31]
list2=[31,29,31,30,31,30,31,31,30,31,30,31]
ye=int(k[0:4])
mon=int(k[4:6])#看来这里不能int，因为02 int后会变成
day=int(k[6:8])
cc=kk=label=0
while 1:
    if isRun(ye):
        li=list2
    else:
        li=list1
    day+=1
    if day>li[mon-1]:
        mon+=1
        day=1
    if mon>12:
        ye+=1
        mon=1
       
    if check(ye,mon,day) and cc==0:
        
        str1=str(ye)+"%02d"%(mon)+"%02d"%(day)
        print(str1)
        cc=1
        
       
        
        
     
    if check2(ye,mon,day) and ~kk:
        kk=1
        str2=str(ye)+"%02d"%(mon)+"%02d"%(day)
        print(str2)
            
        
    label=cc and kk
    if label==1:
        break
       

import calendar
k=input()
#判断闰年
def isRun(strr):
    if strr%400==0 or strr%100!=0 and strr%4==0:
        return 1
def check(ye,mon,day):
    global kk1
    ye=str(ye)
    mon= "%02d"%(mon)
    day= "%02d"%(day)
        
    kk1=ye+mon+day
    if kk1==kk1[::-1]:
        return 1
    
def check2(ye,mon,day):
    global kk2
    ye=str(ye)
    mon= "%02d"%(mon)
    day= "%02d"%(day)
    
        
    kkk=list(ye+mon+day)
    kk2="".join(kkk)

   
    
    if kkk[0]==kkk[2]==kkk[5]==kkk[7] and kkk[1]==kkk[6]==kkk[3]==kkk[4] :
        return 1
    
    
    
list1=[31,28,31,30,31,30,31,31,30,31,30,31]
list2=[31,29,31,30,31,30,31,31,30,31,30,31]
ye=int(k[0:4])
mon=int(k[4:6])#看来这里不能int，因为02 int后会变成
day=int(k[6:8])
cc=kk=label=0
while 1:
    if calendar.isleap(ye):
        li=list2
    else:
        li=list1
    day+=1
    if day>li[mon-1]:
        mon+=1
        day=1
    if mon>12:
        ye+=1
        mon=1
       
    if check(ye,mon,day) and cc==0:
        
       print(kk1)
       cc=1
        
       
        
        
     
    if check2(ye,mon,day) and ~kk:
        kk=1
        print(kk2)
            
        
    label=cc and kk
    if label==1:
        break
       进行优化，处理了一些问题，原来上面我想用函数中的局部变量，可是不会，原来用一个global，就可以了，哈哈哈
       还有bool函数，不用写else return 0， 然后就是标准库calendar.isleap() 就是闰年判断。哈哈。

通过我的努力终于成功了，而且我还学到了很多我不知道的知识，正好梳理一下，不过，就一道题，除了知识之外，还有重要的方法。
我想说，做对题的第一步是仔细阅读，理解正确题意，就这一步是解题的重中之重。我的天啊，我才发现这个AB的是只有两个数，而我却写错了判断条件。呜呜。还有 以后判断 取反值不要用这个~ 还是用赋值和等值判断的好。

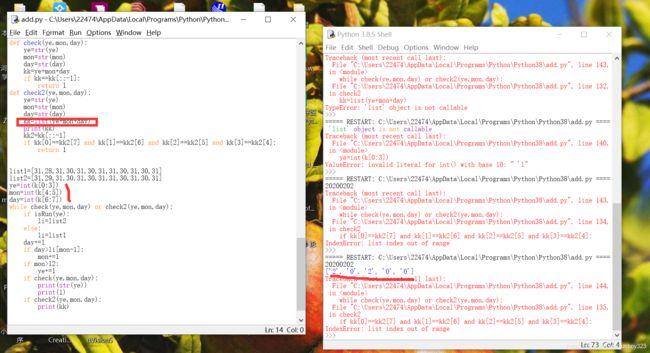
这一次
‘list’ object is not callable 重名

带分数

问题描述
100 可以表示为带分数的形式：100 = 3 + 69258 / 714。

还可以表示为：100 = 82 + 3546 / 197。

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

类似这样的带分数，100 有 11 种表示法。

输入格式
从标准输入读入一个正整数N (N<1000*1000)

输出格式
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。

注意：不要求输出每个表示，只统计有多少表示法！

样例输入1
100
样例输出1
11
样例输入2
105
样例输出2
6

import itertools
n=int(input())
list=[1,2,3,4,5,6,7,8,9];

def getNum(a,b):
        
    num=0
    for i in range(a,b+1):
        
        num=num*10+one[i]
    return num
res=itertools.permutations(list)
ans=0

a=b=c=0
for one in res:
    for i in range(7):#代表循环7次，i依次是0-6
        a=getNum(0,i)
        if a>=n:
            break
        else:
            for j in range(i+1,8):
                b=getNum(i+1,j)
                c=getNum(j+1,8)
                if n==a+b/c and b%c==0 and b>c:
                    ans+=1

                #我终于理解最后一个为啥不用循环，因为c一定要到最后
    ##            for k in range(j+1,9):
    ##                c=getNum(j+1,8)

print(ans)
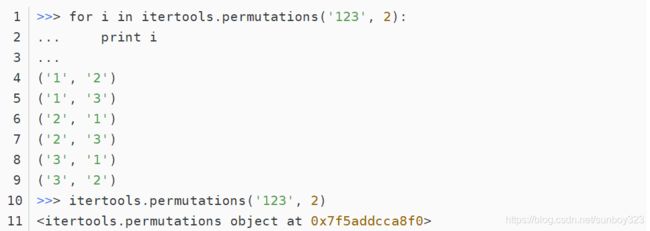
啊，我曾经用这个C++写过这道题，但当时参考大佬的，还是会有一些地方不明白，emm，现在我成功的实现了功能，但是超时了，emm，不过很开心了，还有就是，这个排列，如果你想要显示，只能一个个遍历显示，直接放数组里面显示太多了，会如下图。
 虽然运行超时，但是还是学到了很多。

算法训练

结点选择

链式前向星

for ( init; condition; increment )
{
   statement(s);
}
 for(int i=head[x];i!=-1;i=edge[i].next)
	{
		if(pre==edge[i].to)
		{
			continue;
		}
		int to=edge[i].to;
		dfs(to,x);
		dp[x][0]+=max(dp[to][1],dp[to][0]);
		dp[x][1]+=dp[to][0];
	}

在翻译的过程中，这个可真的是把我难住了，后来我才发现不管是否后面的执行，这个i=edge【i】。next都会执行

#对这个链式前项星还不是很了解，啊，加油。但是我觉得不能再这样，只是眼动了，也得手动起来。

#开始翻译，在翻译的过程中了解把。
maxn=int(1e5+10)
#科学表示法会使浮点

dp=[[0 for i in range(2)]for j in range(maxn)]

head=[-1 for i in range(maxn)]

class node:
    def __init__(self,to=0,nex=0):
        self.to=to
        self.nex=nex
edge=[node() for i in range(maxn*2)]
m=0#边的编号
def add(fro,to):#我好像知道是什么意思了，就是把起点一样的来弄一个联系，就是这个nex，代表现在这条边，它是以u为起点的，nex表示以u为起点的上一条边的编号。我们的编号都储存在head数组里面。
    global m
    
    edge[m].to=to
    edge[m].nex=head[fro]
    
    head[fro]=m
    m+=1


#这个就是深度优先搜索，当他搜到编号为-1，代表以u为起点的
#我好像又明白了，就是这个编号是对应这个权值矩阵的，这个链式前向星就是每一个结构储存前一个的编号，把起点一样的联系在一起，手拉手，

def dfs(x,pre):
    #x此时是起点，pre是前一个点。
    i=head[x]#init
##    print("head【x】",i)
    while i!=-1:#condition
        
        if pre==edge[i].to:
            i=edge[i].nex#increment
            continue
            
        to=edge[i].to
        dfs(to,x)
        dp[x][0]+=max(dp[to][1],dp[to][0])
        dp[x][1]+=dp[to][0]
        i=edge[i].nex#increment
            
    


        


n=int(input())
list=list(map(int,input().split()))

for i in range(1,n+1):
    dp[i][1]=list[i-1] #将权值放到这个选他的时候这个地方，1代表选这个点的最大权值
for i in range(n-1):
    fro,to=map(int,input().split())
    add(fro,to)
    add(to,fro)
##for i in range(9):
##    print("head",i,head[i])
dfs(1,-1)
res=max(dp[1][0],dp[1][1])
    
print(res)
    

安慰奶牛

最小生成树 Krusal算法。并查集

哎哟，真是的，上一次的总结竟然没有被保存，气死我了。我就再写一遍。
这道题不只是最小生成树，还要考虑结点的权值。

#网上没有yhon版本的这道题的解法，但是我学过C++，没事的，我可以翻译。
class e:
    def __init__(sekf,x=0,y=0,d=0):
        sekf.x=x
        sekf.y=y
        sekf.d=d
       #定义这个边的结构，起点编号，终点编号，边的权重。

n,p=map(int,input().split())
tr=[e() for i in range(p)]#  边的权重   重新定义权重 加上点
node=[0 for i in range(n)]#存储点的权重
for i in range(n):
    node[i]=int(input())
for j in range(p):
    x,y,d=map(int,input().split())#这里就是赋值，并重新定义边的权值，因为一定要来回，所以边要走两遍。再加上两个结点。
    tr[j].x,tr[j].y,tr[j].d=x,y,d
    tr[j].d=tr[j].d*2+node[tr[j].x-1]+node[tr[j].y-1]
tr.sort(key= lambda e:e.d)#这一句是关键 将类中的权重按从小到大排序
find=[0 for i in range(n+1)]

for i in range(1,n+1):
    find[i]=i #初始化，每个节点就是一棵树，自已的祖先是自己

def findF(x):#查找根节点  这个并查集有点难理解。
    if find[x]==x:
        return x
    else:
         find[x]=findF(find[x])
         return findF(find[x])
         
        
def Krusal():
   
    ans=0
    k=0
    
    for i in tr:
        father1=findF(i.x)   
        father2=findF(i.y)        
        if father1!=father2:#不是一个祖先，就并到一起
            find[father2]=father1            
            ans+=i.d
            k+=1
            if k==n-1:
                return ans
    
            
aa=Krusal()+min(node)                
print(aa)

Anagrams问题

操作格子

这个很有用 线段树 而且我还又复习了一下全局变量的使用 定义后要在函数内部再次声明。

问题描述
有n个格子，从左到右放成一排，编号为1-n。

共有m次操作，有3种操作类型：

1.修改一个格子的权值，

2.求连续一段格子权值和，

3.求连续一段格子的最大值。

对于每个2、3操作输出你所求出的结果。

输入格式
第一行2个整数n，m。

接下来一行n个整数表示n个格子的初始权值。

接下来m行，每行3个整数p,x,y，p表示操作类型，p=1时表示修改格子x的权值为y，p=2时表示求区间[x,y]内格子权值和，p=3时表示求区间[x,y]内格子最大的权值。

输出格式
有若干行，行数等于p=2或3的操作总数。

每行1个整数，对应了每个p=2或3操作的结果。

样例输入
4 3
1 2 3 4
2 1 3
1 4 3
3 1 4
样例输出
6
3

class tree():
    def __init__(self,l=0,r=0,value=0,maxn=0):
        self.l=l
        self.r=r
        self.value=value
        self.maxn=maxn
k=0
n,m=map(int,input().split())
aa=list(map(int,input().split()))
tr=[tree() for i in range(4*n+1)]
#print(tr)
#print(aa)

def buildtree(root,l,r):
    global k
    tr[root].l=l
    tr[root].r=r
    if l==r:
        
        exm=aa[k]
        k+=1
        tr[root].value=tr[root].maxn=exm
        return
    mid=(l+r)>>1
    buildtree(root<<1,l,mid)
    buildtree(root<<1|1,mid+1,r)
    tr[root].maxn=max(tr[root<<1].maxn,tr[root<<1|1].maxn)
    tr[root].value=tr[root<<1].value+tr[root<<1|1].value
def update(root,what,c):
    if tr[root].l==tr[root].r==what:
        tr[root].maxn=tr[root].value=c
        return
    mid=(tr[root].l+tr[root].r)>>1
    if what<=mid:
        update(root<<1,what,c)
    else:
        update(root<<1|1,what,c)
    tr[root].maxn=max(tr[root<<1].maxn,tr[root<<1|1].maxn)
    tr[root].value=tr[root<<1].value+tr[root<<1|1].value
def query2(root,l,r):
    #print(root)
    if tr[root].l==l and tr[root].r==r:
        return tr[root].value
    mid=(tr[root].l+tr[root].r)>>1
    if r<=mid:
        return query2(root<<1,l,r)
    else:
        if l>mid:
            
            return query2(root<<1|1,l,r)
        else:
            return query2(root<<1,l,mid)+query2(root<<1|1,mid+1,r)
def query1(root,l,r):
    if tr[root].l==l and tr[root].r==r:
        return tr[root].maxn
    mid=(tr[root].l+tr[root].r)>>1
    if r<=mid:
        return query1(root<<1,l,r)
    else:
        if l>mid:
            return query1(root<<1|1,l,r)
        else:
            return max(query1(root<<1,l,mid),query1(root<<1|1,mid+1,r))
        
            
        

buildtree(1,1,n)
for i in range(m):
    a,b,c=map(int,input().split())
    if a==1:
        update(1,b,c)
    if a==2:
        print(query2(1,b,c))

    if a==3:
        print(query1(1,b,c))
        哎呀 终于照着人家的C++版本翻译写出了，这个线段树，哈哈哈，虽然最高不知道原因，还是超时了，哈哈，但是二叉树真的是算法入门最好的这个算法。

哎呀，真头疼，这个线段树又牵扯出了树状数组，真的好难受，不过我终于知道lowbit是啥了，原来是一个数的二进制中最低位1所表示的值。

n,m=map(int,input().split())
lis=list(map(int,input().split()))
def m1(x,y):
    lis[x-1]=y
def m2(x,y):
    ans=0
    for item in lis[x-1:y]:
        ans+=item
    print(ans)
def m3(x,y):
    k=0
    k=max(lis[x-1:y])
    print(k)
for i in range(m):
    a,b,c=map(int,input().split())
    if a==1:
        m1(b,c)
    elif a==2:
        m2(b,c)
    else:
        m3(b,c)
妈呀，还运行超时，只得了50分，
      这道题我还小看了他呢，因为时间的原因，竟然使用了线段树，明天AC。

n1 = input() # 大小写
n2 = input()
n1 = n1.casefold() #全部转换成小写
n2 = n2.casefold()
count = 0
if len(n1) != len(n2):
    print('N')
elif len(set(n1))!=len(set(n2)):
    print('N')
else:
    for i in set(n1):
        if n1.count(i) == n2.count(i):
            count += 1
        else:
            break
    if count == len(set(n1)):
        print('Y')
    else:
        print('N')```
人家全部转了小写，啊，以后我也这样，casefold

a="wijqdQDJ"
print(a.upper())
这个也是可以的，啊啊啊。不用非要casefold upper和lower也是可以的。
```c
m=input()
n=input()
li={}
li1={}
for s in m:
    if s not in li.keys():
        li[s]=1
        if s.isupper():
            li[s.lower()]=1
        else:
            li[s.upper()]=1
        
    else:
        li[s]+=1
        if s.isupper():
            li[s.lower()]+=1
        else:
            li[s.upper()]+=1
        
for s in n:
    if s not in li1.keys():
        li1[s]=1
        if s.isupper():
            li1[s.lower()]=1
        else:
            li1[s.upper()]=1
        
    else:
        li1[s]+=1
        if s.isupper():
            li1[s.lower()]+=1
        else:
            li1[s.upper()]+=1
                    
def check():
    for s in m:
        if li[s]!=li1[s]:
            return 'N'
    return 'Y'
print(check())
我只得了70分，哎呀，真是的，不过我看了一下别人的，啊，人家的满分，而且代码比我短，正好就可以自己先写一下，然后学习下人家的代码。

出现次数最多的整数

编写一个程序，读入一组整数，这组整数是按照从小到大的顺序排列的，它们的个数N也是由用户输入的，最多不会超过20。然后程序将对这个数组进行统计，把出现次数最多的那个数组元素值打印出来。如果有两个元素值出现的次数相同，即并列第一，那么只打印比较小的那个值。
　　输入格式：第一行是一个整数N，N £ 20；接下来有N行，每一行表示一个整数，并且按照从小到大的顺序排列。
　　输出格式：输出只有一行，即出现次数最多的那个元素值。
输入输出样例
样例输入
5
100
150
150
200
250
样例输出
150

n=int(input())
if n>0:
    li={}
    for i in range(n):
        k=int(input())
        if k not in li.keys():
            li[k]=1
        else:
            li[k]+=1
    maxx=0        
    for i in li.keys():
        if li[i]>maxx:
            maxx=li[i]
            ans=i

    print(ans)  
           
也不知道为蛇魔 就得啦八十分，奇怪。
kao,无语，原来要加一个是否n大于0

矩阵乘法

问题描述
　　输入两个矩阵，分别是ms，sn大小。输出两个矩阵相乘的结果。
输入格式
　　第一行，空格隔开的三个正整数m,s,n（均不超过200）。
　　接下来m行，每行s个空格隔开的整数，表示矩阵A（i，j）。
　　接下来s行，每行n个空格隔开的整数，表示矩阵B（i，j）。
输出格式
　　m行，每行n个空格隔开的整数，输出相乘後的矩阵C（i，j）的值。
样例输入
2 3 2
1 0 -1
1 1 -3
0 3
1 2
3 1
样例输出
-3 2
-8 2

提示
矩阵C应该是m行n列，其中C(i,j)等于矩阵A第i行行向量与矩阵B第j列列向量的内积。
例如样例中C(1,1)=(1,0,-1)(0,1,3) = 1 * 0 +01+(-1)*3=-3

m,s,n=map(int,input().split())
##A=[[0 for i in range(s)]for j in range(m)]
##B=[[0 for i in range(n)]for j in range(s)]
#初始化的话 后面就不用append 否则会out of range
A=[]
B=[]
C=[[0 for i in range(m)]for j in range(n)]
for i in range(m):
    A.append(1)
    A[i]=[int(k) for k in input().split()]


for j in range(s):
    B.append(1)
    B[j]=[int(k) for k in input().split()]
#表示是【】【】不是【i，j】
for i in range(m):
    
    for j in range(n):
        tp=0
        for k in range(s):
            tp+=A[i][k]*B[k][j]
        C[i][j]=tp
for i in range(m):
    for j in range(n):
        print(C[i][j],end=" ")
    print()
    
操，也不知道怎么回事，竟然只得了42分，很奇怪，问题出在了哪里呢。

大小写转换

a=input()
rew=[]
for st in a:
    if st.isupper():
        st=st.lower()
    else:
        st=st.upper()
    rew.append(st)
s="".join(rew)
print(s)

动态数组使用

n=int(input())
lis=[int(i) for i in input().split()]
a=sum(lis)
print(a,end=" ")
print(a//n)

关联矩阵

这题就是规律要发现一下
问题描述
　　有一个n个结点m条边的有向图，请输出他的关联矩阵。
输入格式
　　第一行两个整数n、m，表示图中结点和边的数目。n<=100,m<=1000。
　　接下来m行，每行两个整数a、b，表示图中有(a,b)边。
　　注意图中可能含有重边，但不会有自环。
输出格式
　　输出该图的关联矩阵，注意请勿改变边和结点的顺序。
样例输入
5 9
1 2
3 1
1 5
2 5
2 3
2 3
3 2
4 3
5 4
样例输出
1 -1 1 0 0 0 0 0 0
-1 0 0 1 1 1 -1 0 0
0 1 0 0 -1 -1 1 -1 0
0 0 0 0 0 0 0 1 -1
0 0 -1 -1 0 0 0 0 1

m,n=map(int,input().split())
dp=[[0 for i in range(n)]for j in range(m)]
for i in range(n):
    a,b=map(int,input().split())
    dp[a-1][i]=' 1'
    dp[b-1][i]='-1'
for i in range(len(dp)):
    for j in range(len(dp[0])):
        if dp[i][j]==0:
            print(" 0",end=" ")

        else:
            
            print(dp[i][j],end=" ")
    print()
    
哎呀，这个也真是矫情，还非要给他弄成字符串 主要是输出格式需要注意
    

全排列

import itertools

n=int(input())
list=[]
for i in range(1,n+1):
    list.append(i)
for i in itertools.permutations(list):
    for j in i:
        print(j,end=" ")
    print()

分数对等级

结点选择2

这个跟上面那个竟然都是python版70分，但是用的方式不一样，可以说是不同的算法，不过我觉得这个用的字典还挺通俗易懂的，而且写得也挺少的。

看这一张图，其实是这样的，就是当他本身调用本身时，调用一次，就往更深的函数走，但是如果说最深的这一层走不下去了，就开始返回到上一层，并执行完上一层的下面的内容。当上一层也走到了尽头，就回到他的上一层，阻塞打开，执行完剩下的部分。原来是这样。
这道题 最重要的就是 先储存树 然后遍历 使用递归（深度优先遍历 dfs）

#递归 深度搜索真的就很难理解
def dfs(node,pre):
    global value,table
    for i in table.get(node):
        print(i,node,"..1..")
        if i !=pre:
            print(i,node,"..2..")
            dfs(i,node)
            print(i,node,"..3..")
            value[node][0]+=max(value[i][0],value[i][1])
            value[node][1]+=value[i][0]
            print('value["%d"][0]="%d"'%(node,value[node][0]))
            print('value["%d"][1]="%d"'%(node,value[node][1]))

global value, table
n = int(input())
value = list(map(int, input().split()))
value = list(map(lambda x:[0,x],value))

print(value)
value.insert(0,0)
print(value)
table = {}
for i in range(n):
    table.update({i + 1: []})
print(table)
#get(键值)
for i in range(n - 1):
    father, child = list(map(int, input().split()))
    table.get(father).append(child)
    table.get(child).append(father)
print(table)
#以上就是树的储存

dfs(1,0)
print(max(value[1][0],value[1][1]))
哎呀 这道题是真的很难，但是我还是学到了很多，这就是python的优点，他有列表可以嵌套，还有字典，可以用来储存树，好的。
 我今天好像与理解了更深一点，就是递归，其实。

k=int(input())
if k>=90:
    print("A")
if  90>k>=80:
    print("B")
if 80>k>=70:
    print("C")
if 70>k>=60:
    print("D")

if k<60:
    print("E")    

1的个数

问题描述
　　输入正整数n，判断从1到n之中，数字1一共要出现几次。例如1123这个数，则出现了两次1。例如15，那么从1到15之中，一共出现了8个1。
输入格式
　　一个正整数n
输出格式
　　一个整数，表示1出现的资料
样例输入
15
样例输出
8
数据规模和约定
　　n不超过30000

ans=0
n=int(input())
for i in range(1,n+1):
    a=str(i).count("1")
    ans+=a
print(ans)

二进制数数

问题描述
　　给定L,R。统计[L,R]区间内的所有数在二进制下包含的“1”的个数之和。
　　如5的二进制为101，包含2个“1”。
输入格式
　　第一行包含2个数L,R
输出格式
　　一个数S，表示[L,R]区间内的所有数在二进制下包含的“1”的个数之和。
样例输入
2 3
样例输出
3
数据规模和约定
　　L<=R<=100000;

ans=0
m,n=map(int,input().split())
for i in range(m,n+1):
    a=format(i,"b").count("1")
    ans+=a
print(ans)
也可以在这里总结一下了，就是十进制转其他 format（数字，“进制符号”）
						其他转十进制 int（数字，几进制）
					若是其他转其他，先转为10进制，再换	

Luckdays

时间限制：1.0s 内存限制：512.0MB
问题描述
　　厨师夏尔定义了一个数列S，如下所述：
　　S[1]=A
　　S[2]=B
　　S[i]=(XS[i-1]+YS[i-2]+Z)mod P, 对于 i>=3
　　夏尔认为C是一个幸运数字，而且第i天是一个幸运天当且仅当S[i]=C,夏尔的餐厅在幸运天将会有好事发生。你的工作就是计算区间内幸运天的数量。就是说，对每个询问L[i],R[i],你要求出满足L[i]<=k<=R[i]且S[k]=C的k的个数。
输入格式
　　第一行T，表示数据组数。
　　接下来T行，每行8个整数：A,B,X,Y,Z,P,C,Q。接下来Q行每行有两个整数L[i],R[i]。
输出格式
　　对每个询问，输出幸运天的数量。
　　样例输入
2
1 1 1 1 0 2 0 6
1 1
2 2
3 3
4 4
5 5
6 6
1 2 4 5 3 17 4 3
5 8
5 58
58 5858
样例输出
0
1
0
0
1
0
4
362
数据规模和约定
　　1 <= T <= 2
　　2 <= P <= 10007
　　P是一个质数。
　　0 <= A, B, X, Y, Z, C < P
　　1 <= Q <= 20000 (2*10^4)
　　1 <= L[i] <= R[i] <= 1000000000000000000 (10^18)
样例说明
　　对于第一组数据：
　　S[1] = A = 1
　　S[2] = B = 1
　　S[3] = (S[2] + S[1]) mod 2 = (1 + 1) mod 2 = 0
　　S[4] = (S[3] + S[2]) mod 2 = (0 + 1) mod 2 = 1
　　S[5] = (S[4] + S[3]) mod 2 = (1 + 0) mod 2 = 1
　　S[6] = (S[5] + S[4]) mod 2 = (1 + 1) mod 2 = 0
　　S[7] = (S[6] + S[5]) mod 2 = (0 + 1) mod 2 = 1
　　
呜呜呜，我把那个1e8降低，拿了25分，emm，无语。对了这个1e8是一个浮点数，要int。

list=[]

k=int(input())
for i in range(k):
    A,B,X,Y,Z,P,C,Q=map(int,input().split())
    list.append(1) #列表该位置为空不能直接赋值
    list.append(A)
    list.append(B)
   
    for i in range(3,int(1e4)):
        list.append(1)
        list[i]=((X*list[i-1]+Y*list[i-2]+Z)%P)
    for k in range(Q):
        kk=0
        a,b=map(int,input().split())
        for i in range(a,b+1):
            if list[i]==C:
                kk+=1
        print(kk)
啊，这道题也是让我学到了新的知识，就是空列表是不能直接赋值的，但是可以先
for i in range(3,int(1e4)):
        list.append(1)
        list[i]=((X*list[i-1]+Y*list[i-2]+Z)%P)
        弄个1占个位，哈哈
        可是emm，这个结果是对的，可是超时了

加法运算

问题描述
　　你的表妹正在学习整数的加法，请编写一个程序来帮助她学习。该程序调用了一个函数GetTwoInts，由它来返回两个从键盘读入的100以内的整数，然后计算这两个整数之和，并把答案显示出来。要求：在主函数中不能使用scanf等函数直接输入这两个整数，而必须通过调用GetTwoInts函数来完成，在GetTwoInts函数中可以使用scanf函数。另外，由于该函数必须同时返回两个整数，因此不能采用函数返回值的方式，而必须采用指针的方法来实现。
　　输入格式：输入只有一行，即两个100以内的整数。
　　输出格式：输出只有一行，即这两个整数之和。
输入输出样例
样例输入
4 7
样例输出
11

print(sum(list(map(int, input().split()))))
啊，原来这就是python的指针，可以同时返回多个数 而且sum函数只对list有效

字符串合并

问题描述
　　输入两个字符串，将其合并为一个字符串后输出。
输入格式
　　输入两个字符串
输出格式
　　输出合并后的字符串
样例输入
一个满足题目要求的输入范例。
Hello

World
样例输出
HelloWorld

a=input()
b=input()
print(a+b)

笑死了，这种题emm，可能是因为python太方便了

猴子吃包子

格式化输出 print format

问题描述
　　从前，有一只吃包子很厉害的猴子，它可以吃无数个包子，但是，它吃不同的包子速度也不同；肉包每秒钟吃x个；韭菜包每秒钟吃y个；没有馅的包子每秒钟吃z个；现在有x1个肉包，y1个韭菜包，z1个没有馅的包子；问：猴子吃完这些包子要多久？结果保留p位小数。
输入格式
　　输入1行，包含7个整数，分别表示吃不同包子的速度和不同包子的个数和保留的位数。
输出格式
　　输出一行，包含1个实数，表示吃完所有包子的时间。
样例输入
4 3 2 20 30 15 2
样例输出
22.50
数据规模和约定
　　0

list=[]
for s in input().split():
    list.append(int(s))
ans=0
for i in range(3):
    ans+=list[i+3]/list[i]
print("%.{0}f".format(list[6])%ans)
我感觉我的知识模块在不断的完善，emm，格式化输出，这次用到了format的一个作用

删除数组零元素

从键盘读入n个整数放入数组中，编写函数CompactIntegers，删除数组中所有值为0的元素，其后元素向数组首端移动。注意，CompactIntegers函数需要接受数组及其元素个数作为参数，函数返回值应为删除操作执行后数组的新元素个数。输出删除后数组中元素的个数并依次输出数组元素。
样例输入: （输入格式说明：5为输入数据的个数，3 4 0 0 2 是以空格隔开的5个整数）
5
3 4 0 0 2
样例输出:（输出格式说明：3为非零数据的个数，3 4 2 是以空格隔开的3个非零整数）
3
3 4 2
样例输入:
7
0 0 7 0 0 9 0
样例输出:
2
7 9
样例输入:
3
0 0 0
样例输出:
0

k=int(input())
list=[]
ans=0
for s in input().split():
    if int(s)!=0:
        ans+=1
        list.append(int(s))


print(ans)
for item in list:
    print(item,end=" ")

对了，remove应该是偶默认删第一个，但里面写东西了，就删掉他第一个出现的他。

最小乘积(基本型)

同时遍历两个list

问题描述
　　给两组数，各n个。
　　请调整每组数的排列顺序，使得两组数据相同下标元素对应相乘，然后相加的和最小。要求程序输出这个最小值。
　　例如两组数分别为:1 3　　-5和-2 4 1

那么对应乘积取和的最小值应为：
　　(-5) * 4 + 3 * (-2) + 1 * 1 = -25
输入格式
　　第一个行一个数T表示数据组数。后面每组数据，先读入一个n，接下来两行每行n个数，每个数的绝对值小于等于1000。
　　n<=8,T<=1000
输出格式
　　一个数表示答案。
样例输入
2
3
1 3 -5
-2 4 1
5
1 2 3 4 5
1 0 1 0 1

样例输出

-25
6

#原来我想复杂了，就排序，让最大的与最小的相乘
k=int(input())

for i in range(k):
    n=int(input())
    list=[]
    list1=[]
    for s in input().split():
        list.append(int(s))
    for s in input().split():
        list1.append(int(s))
        #做sort变化后，一定要传给原来的变量 我草 这是错的思想 
    list.sort(reverse=True)
    list1.sort()
    

    ans=0
    ##for i in range(len(list)):
    ##    ans+=list[i]*list1[i]
    for (item1,item) in zip(list1,list):
        ans+=item1*item
    print(ans)

哎呀 ，也学了新知识

哎呀刚刚进行了修改，终于知道问题出在哪里了，哈哈哈，前一段时间一直在做难题，现在我终于把这些基本的问题处理了，加油。

Torry的困惑(基本型)

啊，太难了，我用可好长时间才做对，有太多疏忽了，
而且 我意识到 判断有两种
1.一遇到情况就return
2,全部筛过后才能return 而素数判断就是用的这种，就是一有能除尽的就返回0，否则全部筛完了，没有再返回1.
而且真的，思路很重要，当你思路清晰了，然后再把它转化成语句，这也是一种能力呀，要锻炼。

import math

def check(a):# 一碰见 和全部弄完有
    for i in range(2,a):
        if a%i==0:         
            return 0
    return 1

        
k=int(input())
            
a=2#质数
n=1#第几个质数
ans=2#乘积
while n!=k:
    a+=1
    if check(a):
        n+=check(a);
        ans=ans*a
    
print(ans%50000)
而且我发现就是那种直接求取模后的结果只适合加法，递推数列。
我尝试ans=ans*（a%50000）；是错误的。

寻找数组中最大值

问题描述
　　对于给定整数数组a[],寻找其中最大值，并返回下标。
输入格式
　　整数数组a[],数组元素个数小于1等于100。输出数据分作两行：第一行只有一个数，表示数组元素个数；第二行为数组的各个元素。
输出格式
　　输出最大值，及其下标
样例输入
3
3 2 1

样例输出

3 0

k=int(input())
list=[]
for s in input().split():
    list.append(int(s))
print(max(list),end=" ")
print(list.index(max(list)))

K好数 太难了

我草，这个太难了，可能我现在的功力去做这种还特别吃力，哎哎
下面是失败代码，但是我懂这个意思了。以后，再来消化把。
k,l=map(int,input().split())

#创建备忘录
dp=[[0 for i in range(l)]for j in range(k)]#每一行有几个元素，就是前面是内容，后面循环

for i in range(k):
dp[i][0]=1
for i in range(l-1):#先确定位数的位置
for j in range(k):#再确定最高位
kkk=0
for k in range(k):#然后就是低位
if abs(j-k)!=1 or j==k:
kkk+=dp[k][i]

    dp[j][i+1]=kkk

ans=0
for i in range(1,k):
ans+=dp[i][l-1]
print(ans%1000000007)

最大最小公倍数

#我的妈呀，最小公倍数的最大，
只要两个数有一个公因数，则最大公因数一定是相乘再除以这个公因数，比如2,3,4 则为24/2=12 而且紧挨着相邻的两个数一定互质。
1.奇-偶-奇 n为奇数，那么最小公因数一定不是2，假如有一个数含有3这个因数，另外两个也不会含有3，但是,这3个数的跨度也不够3，所以最小公因数也不会是3。后面4,5.。。不可能了 这三个数最大为n,n-1,n-2
2.偶-奇-偶 n为偶数，那么一定会有公因数2，那么最大公倍数会除以2， 不能接受,适当改变,那抹就是n,n-1,n-3.变为奇-偶-奇结构，但是如果n这个偶数中含有因数3，那么就会产生公因数3，那么就变为n-1，n-2，n-3。

k=int(input())
if k%2==0:
    if k%3==0:
        print((k-3)*(k-2)*(k-1))
    else:
        print((k*(k-1)*(k-3)))
else:
    print((k-2)*(k-1)*k)
    太烧脑了
    

区间k大数查询

问题描述
给定一个序列，每次询问序列中第l个数到第r个数中第K大的数是哪个。

输入格式
第一行包含一个数n，表示序列长度。

第二行包含n个正整数，表示给定的序列。

第三个包含一个正整数m，表示询问个数。

接下来m行，每行三个数l,r,K，表示询问序列从左往右第l个数到第r个数中，从大往小第K大的数是哪个。序列元素从1开始标号。

输出格式
总共输出m行，每行一个数，表示询问的答案。
样例输入
5
1 2 3 4 5
2
1 5 2
2 3 2
样例输出
4
2
数据规模与约定
对于30%的数据，n,m<=100；

对于100%的数据，n,m<=1000；

保证k<=(r-l+1)，序列中的数<=106。

def get(l,r,k,list2):
    list1=[]
    list1=list2[l-1:r]
    list1.sort(reverse=True)
    
    print(list1[k-1])
list=[]       
n=int(input())
for s in input().split():
    list.append(int(s))
m=int(input())
for i in range(m):
    l,r,k=map(int,input().split())
    get(l,r,k,list)
哈哈哈，这一题用到了切片，我才发现切片的下标位置也是左闭右开。

基础练习

Fibonacci数列

在本题中，答案是要求Fn除以10007的余数，因此我们只要能算出这个余数即可，而不需要先计算出Fn的准确值，再将计算的结果除以10007取余数，直接计算余数往往比先算出原数再取余简单。
算出了原数导致内存超限
是的 ，大家不难发现，经常有这种递推数列，然后，到了很大的一个数让你做一个简单的计算，可是内存或者用时会超。所以，直接求结果。

问题描述
Fibonacci数列的递推公式为：Fn=Fn-1+Fn-2，其中F1=F2=1。

当n比较大时，Fn也非常大，现在我们想知道，Fn除以10007的余数是多少。

输入格式
输入包含一个整数n。
输出格式
输出一行，包含一个整数，表示Fn除以10007的余数。
说明：在本题中，答案是要求Fn除以10007的余数，因此我们只要能算出这个余数即可，而不需要先计算出Fn的准确值，再将计算的结果除以10007取余数，直接计算余数往往比先算出原数再取余简单。

样例输入
10
样例输出
55
样例输入
22
样例输出
7704
数据规模与约定
1 <= n <= 1,000,000。

def fei(k):
    a=1
    b=1
    for i in range(3,k+1):
        if k>=1 and k<=1000000000:
            c=a+b
            a,b=b,c%10007

    return b;
print(fei(int(input())))
而且这个封装函数，会使速度变快。
        

A+B问题

样例输入
12 45
说明：“样例输入”给出了一组满足“输入格式”要求的输入的例子。

这里给出的输入只是可能用来测试你的程序的一个输入，在测试的时候，还会有更多的输入用来测试你的程序。

样例输出
57

a,b=map(int,input().split())
print(a+b)
这个还是在处理空格这个问题，和前面的数列排序差不多

序列求和

求1+2+3+…+n的值。
输入格式
输入包括一个整数n。
输出格式
输出一行，包括一个整数，表示1+2+3+…+n的值。
样例输入
4
样例输出
10
样例输入
100
说明：有一些试题会给出多组样例输入输出以帮助你更好的做题。

一般在提交之前所有这些样例都需要测试通过才行，但这不代表这几组样例数据都正确了你的程序就是完全正确的，潜在的错误可能仍然导致你的得分较低。

样例输出
5050
数据规模与约定
1 <= n <= 1,000,000,000。

k=int(input())
a=0;
for i in range(1,k+1):
    a+=i
print(a)
上面运行超时
运行成功
k=int(input())
if k>=1 and k<=1000000000:
    a=(k**2+k)/2
print(int(a))
用公式就可以不超时了，因为那个暴力相加，就耗时较多。 而且如雇用触发，结果是浮点数

圆的面积

问题描述
给定圆的半径r，求圆的面积。
输入格式
输入包含一个整数r，表示圆的半径。
输出格式
输出一行，包含一个实数，四舍五入保留小数点后7位，表示圆的面积。
说明：在本题中，输入是一个整数，但是输出是一个实数。

对于实数输出的问题，请一定看清楚实数输出的要求，比如本题中要求保留小数点后7位，则你的程序必须严格的输出7位小数，输出过多或者过少的小数位数都是不行的，都会被认为错误。

实数输出的问题如果没有特别说明，舍入都是按四舍五入进行。

样例输入
4
样例输出
50.2654825
数据规模与约定
1 <= r <= 10000。
提示
本题对精度要求较高，请注意π的值应该取较精确的值。你可以使用常量来表示π，比如PI=3.14159265358979323，也可以使用数学公式来求π，比如PI=atan(1.0)*4。

import math
r=int(input())
s=math.pi*r**2
print("%.7f"%s)

数列排序

问题描述
　　给定一个长度为n的数列，将这个数列按从小到大的顺序排列。1<=n<=200
输入格式
　　第一行为一个整数n。
　　第二行包含n个整数，为待排序的数，每个整数的绝对值小于10000。
输出格式
　　输出一行，按从小到大的顺序输出排序后的数列。
样例输入
5
8 3 6 4 9
样例输出
3 4 6 8 9

天哪 下面这个不可以，是因为输入必须是1行，而我这个每输入1个就需要换行，

天哪，input().split()的类型竟然是list，而int（）里面需要是string。

以空格分割输入多个数存入列表

哎呀，其实这一题最难的就是格式问题。
终于成功了

list=[];
k=int(input());
for i in range(k):
    list.append(int(input()));

list.sort(); #默认从小到大
print(list);
错

list=[];
k=int(input());
for item in input().split():
    list.append(int(item))
list.sort()
for item in list:
    print(item,end=" ")

###特殊的数字
问题描述
　　153是一个非常特殊的数，它等于它的每位数字的立方和，即153=111+555+333。编程求所有满足这种条件的三位十进制数。
输出格式
　　按从小到大的顺序输出满足条件的三位十进制数，每个数占一行。

list1 = []
def get(n):

    a=n%10
    b=(int(n/10))%10
    c=(int(n/100))%10
    if n==a*a*a+b*b*b+c*c*c:
        list1.append(n)
for i in range(100,1000):
    get(i)
for i in range(len(list1)):
    print(list1[i],end="") #这里真是作妖 单纯的print设置空格为输出空格，结尾为换行，不过也可以指定。
    print()

而且这个他不是像C那样a/100 是舍去后面小数部分，得到一个整数，而是double类型。

回文数

list=[]
def get(n):
    w=n%10
    ww=(int(n/10))%10
    www=(int(n/100))%10
    wwww=(int(n/1000))%10
    if w==wwww and ww==www:
        list.append(n)
for i in range(1000,10000):
    get(i)
# for i in range(len(list)):
#     print()
for item in list:
    print(item)

特殊回文数

import  time
n=int(input())
start=time.clock()

def is_hui(k):
    strr=str(k)
    if strr==strr[::-1]:
        return True
    else:
        return False
def summ(k):
    std=str(k)
    sum=0
    for item in std:
        sum+=int(item)
    return  sum
for i in range(10000,1000000):
    if is_hui(i):
        if summ(i)==n:
            print(i)
end=time.clock()
print(end-start)

转进制 用python 一句话的事情

进制转换

n=int(input())
k=input()
print(format(n,"X"))# 10进制转16进制
print(int(k,16))#16进制转10进制 而且这个输入必须是字符串

#16转8 16先转10，再转8
s=input()
k=int(s,16)
print(format(k,"o"))

十六进制转八进制

资源限制
时间限制：1.0s 内存限制：512.0MB
问题描述
　　给定n个十六进制正整数，输出它们对应的八进制数。

输入格式
　　输入的第一行为一个正整数n （1<=n<=10）。
　　接下来n行，每行一个由0_{9、大写字母A}F组成的字符串，表示要转换的十六进制正整数，每个十六进制数长度不超过100000。

输出格式
　　输出n行，每行为输入对应的八进制正整数。

【注意】
　　输入的十六进制数不会有前导0，比如012A。
　　输出的八进制数也不能有前导0。

样例输入
　　2
　　39
　　123ABC

样例输出
　　71
　　4435274

【提示】
　　先将十六进制数转换成某进制数，再由某进制数转换成八进制。

n=int(input())
for i in range(n):
    k=input()
    print(format(int(k,16),"o"))

汇编语言听起来真的那啥，还是要亲自编一下，嗯。原来Dosbox是模拟的，哈哈 好吧 我要加油了
真是的，我能拿奖就怪了，你看才做了多少，而且吸收又不能100%，哎。没事，知道失败的经验就行了，其实看经验贴，最重要的是看失败的经验贴。