机器学习实战2-决策树算法

开发环境是：jupyter lab需要的库可以自行百度安装

决策树算法核心是要解决两个的关键问题

1、如何从数据表中照出最佳节点和最佳分支
2、如何让决策树停止生长防止过拟合

就是说假如我有一张数据表，数据表中有成千上万个特征，我要把他们都提问完吗？

sklearn中的决策树模型

本文主要是学习分类树和回归树

sklearn建模步骤

from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf = clf.fit(x_train, y_train)
result = clf.score(x_test, y_test)

分类树

Criterion

为了将表格转化为一棵树，决策树需要找到最佳节点和最佳分支方法，对于分类数来说衡量最佳的方法是叫做不纯度，通常来说不纯度越低，决策树对训练集的拟合效果越好，所有的决策树算法都是将和不纯度相关的某个属性最优化，不管我们用那个算法，都是追求的与不纯度相关的指标最优化
不纯度基于节点来计算，树中的每个节点都会有一个不纯度，并且子节点的不纯度一定低于父节点的不纯度，在一棵决策树上叶子节点的不纯度一定是最低的

Criterion这个参数就是用来决定不纯度计算方法的，sklearn中提供了两种方法
一种是输入“entropy”，使用信息熵
一种是输入"gini",使用基尼系数

我们无法干扰信息熵和基尼系数的计算，所以这里我们知道怎么算的即可，sklearn中的方法我们是无法干扰的
相比于基尼系数来说，信息熵对于不纯度更加敏感，对不纯度的更强，但在实际使用中两者的效果差不多，信息熵的计算相比于基尼系数会慢一点，因为基尼系数没有对数运算，因为信息熵对于不纯度更加敏感，所以信息熵在计算决策树时候会更加仔细，所以对于高维数据或者噪音很多的数据来说很容易过拟合
关于参数如何选择


我们可以看到我们的决策树中并没有用到我们所给的所有属性

clf = tree.DecisionTreeClassifier(criterion = "entropy", random_state=30)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest) # 返回预测的准确度accuracy
score

random_state && splitter

用来设置分支中的随机模式的参数，默认为None，在高维度时随机性会表现更明显，低维度数据几乎不会显现，我们任意给random_state一个数值可以让模型稳定下来
决策树是随机的
splitter也是用来控制决策树中随机选项的可以输入best，决策树虽然分支时会随机但会有限选择更重要的特征进行分支，输入random分支时会更加随机，树会更深，拟合将会降低，这也是防止过拟合的一种方法

clf = tree.DecisionTreeClassifier(criterion = "entropy", splitter="best")
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest) # 返回预测的准确度accurac
score

剪枝参数

在不加限制的情况下，一颗决策树会生长到衡量不纯度的指标最优，或没有更多的特征可用停止，这样的决策树往往会过拟合，也就是说他会在训练集上表现很好，在测试集上表现却很糟糕

score = clf.score(Xtrain, Ytrain)
score

我们要分清楚过拟合的概念，过拟合，也就是说他会在训练集上表现很好，在测试集上表现却很糟糕，但如果我们在训练集和测试集上的表现效果都很好的话不能称为过拟合

剪枝策略对于决策树的影响巨大，正确的剪枝策略是决策树优化的核心

max_depth

限制树的最大深度，超过设定深度的树枝全部剪掉
这是用的最广泛的剪枝参数，在高维度低样本量时非常有效，决策树多生长一层对样本的需求量就会增加一倍，所以限制决策树的深度能够特别有效的限制过拟合，在集成算法中也非常常用，在实际使用过程中，建议我们从3开始尝试，看看拟合的效果再决定是否增加深度

min_samples_leaf&&min_samples_split

这两个是用来限制叶子节点的参数，
min_samples_leaf建议从5开始使用
min_samples_split：一个节点至少包含min_samples_split个样本才被允许进行分支

max_features&&min_impurity_decrease

确认最优剪枝参数

使用确认超参数的曲线

import matplotlib.pyplot as plt
test = []
for i in range(10):
    clf = tree.DecisionTreeClassifier(criterion = "entropy"
                                      , random_state=30
                                      , splitter="random"
                                      , max_depth = i + 1
                                     )
    clf = clf.fit(Xtrain, Ytrain)
    score = clf.score(Xtest, Ytest) # 返回预测的准确度accuracy
    test.append(score)
plt.plot(range(1,11), test,color = "red", label="max_depth")
plt.legend()
plt.show()

目标权重参数

重要属性和接口

fit
score
apply
predict

回归树

参数、属性、接口

Criterion

回归树衡量分枝质量的指标，支持的有三种
1、mse使用均方误差
2、friedman_mse误差费尔德曼均方误差
3、mae绝对均方误差
这里面也有许多数学原理，但是我们在使用sklearn时不用关心，因为这些因素我们并无法干预

属性依然是feature_importance_
接口中依然是
fit
score
apply
predict
是最核心

交叉验证

交叉验证是用来验证模型稳定性的一种方法，我们将数据划分为n份，依次使用其中一份作为测试集，其他n-1份作为训练集，多次计算模型的精确性来评估模型的平均准确程度

导入所需要的库

from sklearn.datasets import load_diabetes
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor

导入数据集

diabetes = load_diabetes()

实例化并交叉验证

regressor = DecisionTreeRegressor(random_state = 0) #实例化
cross_val_score(regressor
				, diabetes.data
				, diabetes.target
				, cv = 10
				, scoring = "neg_mean_squared_error") #交叉验证

参数解读
1、第一个参数可以是回归也可以是分类，这里的模型不止可以是决策树，可以是其他的支持向量机、随机森林等等模型，可以是任何我们实例化后的算法模型
2、第二个参数是完整的不需要分测试集和训练集的特征矩阵，交叉验证会自己帮我们划分测试集和数据集
3、第三个参数是数据的标签（完整的数据标签）
4、cv = 10是将数据集分成10分，每次用其中的一份作为测试集，通常我们将这个数设为5
5、scoring用后面的neg_mean_squared_error衡量我们交叉测试的结果，当默认时会返回R^{2可能为负数，但是我们在做回归时最常用的是均方误差，neg_mean_squared_error是负均方误差，R}2越接近1越好

sin函数模拟实例（回归树）

导入库

import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

随机种子

rng = np.random.RandomState(1)

生成数据

x = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(x).ravel() # 降维使我们的数据只有一维
# y = np.sin(x).ravel()我们现实中不可获得的数据的真实的状况，所以我们需要加入一些噪声
print(y.shape)
y[::5] += 3 * (0.5 - rng.rand(16)) # 这里涉及切片的用法，行、列、最后一个是步长，这里表示对所有的数进行步长为5的切片，这一步是添加噪声

作图

plt.figure()
plt.scatter(x, y, s= 20, edgecolor = "black", c = "darkorange", label = "data")

不包含噪声的图

包含噪声的图

降维函数ravel()的使用、

实例化模型

regr_1 = DecisionTreeRegressor(max_depth = 2)
regr_2 = DecisionTreeRegressor(max_depth = 5)
regr_1.fit(x, y)
regr_2.fit(x, y)

生成测试集

X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
# 用numpy生成的随机数

np.arange(开始点, 结束点, 步长)

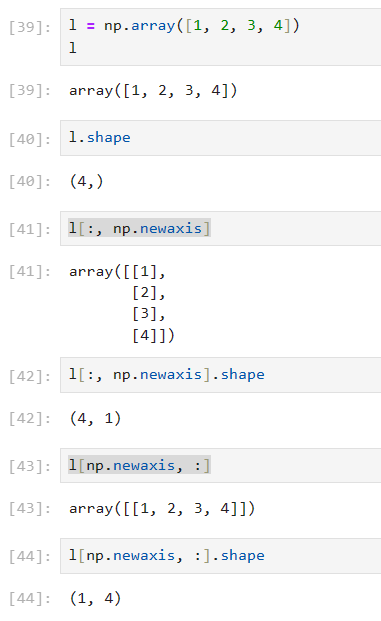
增维切片np.newaxis

作图

plt.figure() # 告诉python我们要画图了，让他帮我们生成一张画布
plt.scatter(x, y, s = 20, edgecolor = "black", c = "darkorange", label = "data")
## 画的是我们两个回归模型的结果
plt.plot(X_test, y_1, color = "cornflowerblue", label = "max_depth = 2", linewidth=2)
plt.plot(X_test, y_2, color = "yellowgreen", label = "max_depth = 5", linewidth=2)
## 横坐标的名称
plt.xlabel("data")
## 纵坐标的名称
plt.ylabel("target")
# 图的名称
plt.title("Decision Tree gression")
# 显示图例
plt.legend()

plt.show()

案例：泰坦尼克号幸存者的预测

导库

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
import matplotlib as plt
from sklearn.model_selection import GridSearchCV

读入数据

data = pd.read_csv(r"C:\Users\cxy\OneDrive\桌面\titanic\train.csv") #加r之后不用将里面面向左的下划线改成向右的

数据如下图

数据来源于坦坦尼克号数据集
观察我们的数据集，我们的标签一般我们习惯上放在最后一列，但是在这个数据集中并不是在最后一列所以这里我们用切片的方式将标签提取出来
我们先来探索数据

data.info()

我们的数据集一共有891行0到890是我们的索引，
我们还可以观察到我们的这些标签中有很多不是数字类型的，有很多类类型，而我们的分类器是不能处理这些数据类型的
我们还可以观察到表中还有很多缺失值，例如年龄这些都是需要我们去处理的

#显示前几行数据，可以有一个参数n，如果不填默认是5，可以有效地帮我查看表的样式
data.head()

数据预处理

筛选特征

data.drop(['Cabin', "Name", "Ticket"], inplace = True, axis = 1)

删除名为’Cabin’, “Name”, "Ticket"的列， inplace = True这个参数的作用是用新生成的表覆盖原表，axis=1表示对列进行操作

处理缺失值

我们可以看到当我筛选完特征之后数据中依然含有一些特征是有很多的缺失值的，所以这时我们要对这些缺失值进行处理

data['Age'] = data['Age'].fillna(data['Age'].mean())

这里我们对于这种缺失值的处理使用年龄的平均值去进行处理的，这里也给我们的数据添加了一些噪声，对于有些缺失值我们也可以直接用0去填补

可以看到我们填充之后年龄这一属性就没有缺失值了
这里我们再次观察我们的数据集，我们会发现Embarked这一属性还是有缺失值，但是缺失值只有几个比较少，我们就直接把那几个缺失值的行给删去即可

data = data.dropna(axis = 0)

处理数据类型

我们知道决策树是处理不了文字类型的所以遇到文字类型，我们需要处理这些文字类型的数据
unique（）方法是对数据进行去重，我们就可以得到这个数据有多少种取值

data['Embarked'].unique()

data['Embarked'].unique().tolist()

这里tolist()方法可以将array转化为list

data['Embarked'].apply(lambda x : labels.index(x))

labels.index("S")

只要我们unique()后的数据不超过10个我们都可以用这种方式来处理数据，前提是我们的数据之前没有联系就比如我们的S、Q、C中的数据没有任何关系

对于性别的处理我们仍然可以按照上述方式不过这里性别是二分类，我们可以另一种方式去处理

data.loc[:,"Sex"] = (data["Sex"] == "male").astype("int")

数据处理完之后我们就可接着回到sklearn了，sklearn中特征和标签是分开的，所以这里我们也需要将特征和标签分开

x = data.iloc[:, data.columns != "Survived"]

y = data.iloc[:, data.columns == "Survived"]

数据集的划分

Xtrain, Xtest, Ytrain, Ytest = train_test_split(x, y, test_size = 0.3)

我们可以看到由于我们的数据集是随机划分的，所以划分完之后的索引也变乱了，如果我们不是刻意需要保持索引的乱序，我们一般来说需要将索引调整为升序

Xtrain.index = range(Xtrain.shape[0])

for i in [Xtrain, Xtest, Ytrain, Ytest]:
    i.index = range(i.shape[0])

因为有四组数据我们可以直接用循环来处理

索引的处理是很重要的，我们只要在进行了某些随机操作，为了避免后续出错一般来说都需要将索引恢复到正常

至此我们将数据处理的所有工作完成，下面我们就可以开始跑模型了

模型的建立

实例化模型

clf = DecisionTreeClassifier(random_state=30)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)

score

交叉验证

from sklearn.model_selection import cross_val_score
clf = DecisionTreeClassifier(random_state=25)
# mean()是求均值的方法
score = cross_val_score(clf, x, y, cv = 10).mean()
score

我们可以看到这里平均得分相比于我们上面随机划分的数据集得分低，这说明我们随机划分的数据集比较好，接下来我们就需要通过调参来将模型的得分调高

调参

画超参数的曲线

import matplotlib.pyplot as plt 
te = []
tr = []
for i in range(10):
    clf = DecisionTreeClassifier(random_state = 25
                                ,max_depth = i + 1)
    clf = clf.fit(Xtrain, Ytrain)
    score_tr = clf.score(Xtrain, Ytrain)
    score_te = cross_val_score(clf, x, y, cv = 10).mean()
    tr.append(score_tr)
    te.append(score_te)
print(max(te))
plt.plot(range(1, 11), tr, color = "red", label = 'train')
plt.plot(range(1, 11), te, color = 'blue', label = 'test')
plt.xticks(range(1, 11))
plt.legend()
plt.show()

我们可以看到随着树的层数的加深，过拟合的程度越来越严重，我可以看到极值点在3这说明在max_depth = 3的时候过拟合程度是最小的，所以我们就需要将max_depth固定在3然后i去调节其他参数
我们可以看到当我们将criterion设置为entropy后score会有怎样的变化

import matplotlib.pyplot as plt 
te = []
tr = []
for i in range(10):
    clf = DecisionTreeClassifier(random_state = 25
                                ,max_depth = i + 1
                                ,criterion = 'entropy'
                                )
    clf = clf.fit(Xtrain, Ytrain)
    score_tr = clf.score(Xtrain, Ytrain)
    score_te = cross_val_score(clf, x, y, cv = 10).mean()
    tr.append(score_tr)
    te.append(score_te)
print(max(te))
plt.plot(range(1, 11), tr, color = "red", label = 'train')
plt.plot(range(1, 11), te, color = 'blue', label = 'test')
plt.xticks(range(1, 11))
plt.legend()
plt.show()

可以看到我们模型的结果变好了
我们仍需要剪枝调参，我们不可能一个一个的画学习曲线，找出最优的组合，这里我们就要引入一个新的知识点叫网格搜索

网格搜索

网格搜索能够帮助我们一次调节多个参数的技术，枚举的思路
缺点：计算量很大，这时由于枚举本身就很耗时

linspace和arange的区别
linspace是随机的，arange是指定步长

import numpy as np
# 在给定的数据范围内取出指定个有顺序的随机数
jini_threholds = np.linspace(0, 0.5, 50)
# enproty_threholds = np.linspace(0, 1, 50)

# 一些参数和这些参数对应的，我们希望网格搜索来搜索的参数的取值范围
parameters = {"criterion" : ("gini", "rntropy")
              ,"splitter" : ("best", "random")
              ,"max_depth"  : [*range(1, 10)]
              ,"min_samples_leaf":[*range(1, 50, 5)]
              ,"min_impurity_decrease" : [*np.linspace(0, 0.5, 50)]
              
}

clf = DecisionTreeClassifier(random_state = 25)
GS = GridSearchCV(clf, parameters, cv = 10) # 同时满足了fit, score, 交叉验证三种功能
GS = GS.fit(Xtrain, Ytrain)

网格搜索模型中的参数（两个比较重要的参数）

GS.best_params_ #从我们输入的参数和参数取值的列表中，返回最佳组合
GS.best_score_ #网格搜索后的模型的评判标准