第二章 算法分析

系列文章目录

目录

• 引论：算法
• 2.1   数学基础
• 2.2   模型
• 2.3   要分析的问题
• 2.4   运行时间计算

---

前言

这一章我们将讨论：

• 如何估计一个程序所需要的时间
• 如何将一个程序的运行时间从天或年降低到秒
• 粗心地使用递归的后果
• 将一个数自乘得到其幂以及计算两个数的最大公因数的非常有效的算法

---

引论：算法

算法(algorithm)是为求解一个问题需要遵循的、被清楚地指定的简单指令的集合。对于一个问题，一旦给定某种算法并且(以某种方式)确定其是正确的，那么重要的一步就是确定该算法将需要多少诸如时间或空间等资源量的问题。如果一个问题的求解算法需要长达一年的时间，那么这种算法就很难有什么用处。同样，一个需要1GB内存的算法在当前的大多数机器上也是无法使用的。

2.1   数学基础

1.定义：相对增长率（relative rate of growth）

（1）若存在正常数和使得当时，则记为，大O记法

的增长率小于等于（）的增长率

是的上界（upper bound）

（2）若存在正常数和使得当时，则记为，

的增长率大于等于（）的增长率

是的下界（lower bound）

（3）当且仅当且时，

的增长率等于（）的增长率

（4）若且，则，小o记法

的增长率小于（）的增长率

注：根据上下文等选择最好的答案

2.法则：

（1）若且，则

（a）

（b）

（2）若是一个次多项式，则

（3）对任意常数，，对数增长得非常缓慢

注：在大O记法中，常数和低阶项一般可以忽略

函数	名称
	常数
	对数级
	对数平方根
	线性级
	平方级
	立方级
	指数级

图2-1      典型的增长率

3.极限确定相对增长率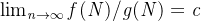：，洛必达法则等

（1），

（2），

（3）为，

（4）极限摆动，二者无关

注：，无意义，定义已经隐含不等式

2.2   模型

      为了在正式的框架中分析算法，我们需要一个计算模型。我们的模型基本上是一台标准的计算机，在机器中顺序地执行指令。该模型有一个标准的简单指令系统，如加法、乘法、比较和赋值等。但不同于实际计算机情况的是，模型机做任意一件简单的工作都恰好花费一个时间单元。为了合理起见，我们将假设该模型像一台现代计算机那样有固定范围的整数（比如32位）并且不存在诸如矩阵求逆或排序等运算，他们显然不能再一个时间单元内完成。我们还假设模型机有无限的内存。

      显然，这个模型有些缺点。很明显，在现实生活中不是所有的运算都恰好花费相同的时间。特别是在该模型中，一次磁盘读入计时同一次加法，虽然加法一般要快几个数量级。还有，由于假设有无限的内存，我们再也不用担心缺页中断，它可能是个实际问题，特别是对高效的算法。

2.3   要分析的问题

1.运行时间

（1）要分析的最重要的资源一般就是运行时间

（2）有几个因素影响着程序的运行时间：有些因素（如使用的编译器和计算机）显然超出了任何理论模型的范畴，因此，虽然他们是重要的，但是我们再这里还不能处理他们；剩下的主要因素则是所使用的算法以及对该算法的输入。

（3）通常，输入的大小时主要的考虑方面。定义函数：

：输入为N时算法所花费的平均运行时间

：最坏情况下的运行时间

若存在更多的输入，则这些函数可以有更多的变量

（4）一般来说，若无另外的指定，则所需要的量是最坏情况下的运行时间。其原因之一是它对所有的输入提供了一个界限，包括特别坏的输入，而平均情况分析不提供这样的界。另一个原因是平均情况的界计算起来通常要困难得多。在某些情况下，“平均”的定义可能影响分析的结果。

2.最大子序列和问题

      给定整数（可能有负数），求的最大值（为方便起见，若所有整数均为负数，则最大子序列和为0）

2.4   运行时间计算

1.简化分析     

      为简化分析，我们采纳如下的约定：不存在特定的时间单元。因此，我们抛弃前导常数和低阶项，计算大O运行时间。有于大O是一个上界，我们必须仔细，绝不要低估程序的运行时间。实际上，分析的结果为程序在一定时间范围内能够终止运行提供了保障。程序可能提前结束，但绝不可能延后。

2.一个简单的例子

计算的一个简单的程序片段：

int Sum(int N)
{
        int i, PartialSum;

/*1*/        PartialSum = 0;
/*2*/        for (i = 1; i <= N; i++)
/*3*/             PartialSum += i * i * i;
/*4*/        return PartialSum;
}

（1）声明不计时间

（2）第1行和第4行各占用一个时间单元

（3）第3行每执行一次占用4个时间单元（两次乘法、一次加法和一次赋值），而执行N次共占用4N个时间单元。

（4）第2行在初始化i、测试i <= N和对i的自增运算中隐含着开销。初始化占一个时间单元，所有的测试占N+1个时间单元，以及所有的自增运算占N个运算单元，共2N+2个时间单元。

（5）忽略调用函数和返回值的开销，得到的总量是6N+4，所以该函数是的

3.一般法则

（1）for循环：一次for循环的运行时间至多是该for循环内语句（包括测试）的运行时间乘以迭代的次数。

（2）嵌套的for循环：从里向外分析这些循环。在一组嵌套循环内部的一条语句总的运行时间为该语句的运行时间乘以该组所有的for循环的大小的乘积。

如下列程序片段的运行时间为：

    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            k++;

（3）顺序语句：将各个语句的运行时间求和即可（其中的最大值就是所得的运行时间，见2.1节的法则1（a））

如下列程序片段先用去，再花费，总的开销也是：

  for (i = 0; i < N; i++)
        A[i] = 0;
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            A[i] += A[j] + i + j;

 （4）if/else语句：一个if/else语句的运行时间从不超过判断的时间加上S1和S2中运行时间较长者的总的运行时间（对下列的程序片段）

if (Condition)
    S1
else
    S2

（5）其他法则：从内部（或最深层部分）向外展开；若有函数调用，首先分析；若有递归过程：若只是稍加掩饰的for循环，则分析通常是很简单的，如下列的函数实际上就是一个简单的循环，运行时间为

long int
Factorial(int N)
{
    if (N <= 1)
        return 1;
    else
        return N * Factorial(N - 1);
}

总结

提示：这里对文章进行总结：

例如：以上就是今天要讲的内容，本文简单介绍了算法分析的基本步骤和公式。