强化学习(3):DQN及其变式
本章内容主要参考了UC Berkeley Deep RL Bootcamp的内容,由作者按照自己的理解整理而成
本讲讨论著名的DQN算法(Deep Q-Networks Algorithm)
一、对Q-Learning的简单复习
对于参数化后的Q函数 Q θ ( s , a ) Q_\theta(s,a) Qθ(s,a),其自变量是当前所在的状态与进行的动作的组合,函数值代表这种组合对应的奖励值的大小。在进行学习迭代更新的时候采用逐步更新,逼近target的方式进行处理,其中target代表使用greedy方法,利用当前第k轮次Q函数确定的当前状态当前动作对应的奖励值的最优情况,我们引入学习率之后使用梯度方法逐步逼近target,用s‘给s赋值后重复这一过程。其中参数化的方式有很多种,其中一个特殊情况( n = ∣ S ∣ ⋅ ∣ A ∣ n=|S| \cdot |A| n=∣S∣⋅∣A∣)则退化成了Tabular Q-Learning,即用一张表格记录下所有可能的Q函数取值情况,这时每次更新只会对s,a对应的唯一参数产生影响,进行化简可以得到退化后的Tabular Q-Learning的迭代更新表达式。具体的过程如下图所示
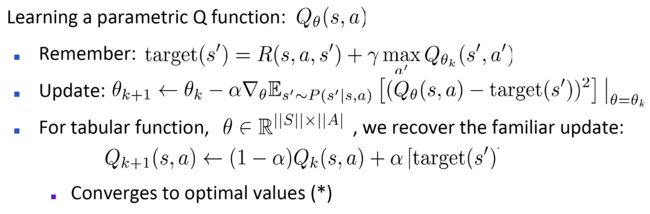
其中需要注意,对于tabular Q-Learning,每次更新Q函数之后相比于更新之前只对一个(s, a)组合的Q函数进行了改变,其他组合并没有发生变化;但是一般的Approximate Q-Learning中进行更新时虽然出发点是对一个特定(s, a)组合的Q值进行修正,但是由于参数化对状态进行了概括归纳(generalize),这种改变同样会影响其他的状态-动作组合的Q函数值。本讲中我们着重考虑的情况是,由于参数化的方式十分多样难以选到合适的,不妨采用神经网络的方式对Q函数进行模拟,即确定一个Q-Network,输入是当前状态s与选择的动作a,输出是 Q ( s , a ) Q(s,a) Q(s,a),参数即为网络的权重参数。但是DQN算法并不能简单地Approximate Q-Learning的方法中参数化的方式改成使用神经网络,参数是网络权重,这样会面临一些困难,在接下来的部分将会具体分析DQN针对这些问题的解决方法,也就是DQN的独特创新之处。
二、DQN算法
正如左图所示,直接用神经网络替换模拟函数主要会面临两个困难。第一个是不稳定性,正如上边所分析的那样,由于每次更新不仅会改变当前状态-动作组合的Q函数值,由于generalize的特点,同样也会改变其他状态-动作组合的Q函数值,因此一个现在已经“调好”的合适Q函数值也可能在对别的状态进行调整的时候再度被改变,离开已经处在的最优情况。另一个困难是更新和路径相关,或者说更新被限制在路径之内,这对整体的探索和学习来说并不是一件好的事情。
DQN算法的高层观点(High-level idea)是:使Q-Learning看起来更像supervised learning,为了提升稳定性,有两个关键的技术手段,一个是replay buffer,另一个是target network
(1)replay buffer
之前所描述的一般的Q-Learning采用online update的方法进行更新,也就是伴随着学习过程的进行,每走一步(state变化一次)就会对Q网络进行一次更新,但是这种更新过于频繁,是导致不稳定情况出现的原因之一。因此我们引入replay buffer来降低更新的频次。具体来说,我们把每次状态的transition pair(s, a, s’, r)组合存入有一定容量限制的replay buffer中,随着探索的不断进行buffer中数据量的规模也在不断增大,在加入新的pair的时候也会讲旧的pair删除,最终将buffer中的数据量维持在一个合适的规模(一般是one million左右)。在学习更新Q网络的时候,对buffer中的pairs进行采样(比如采样32个pairs),之后就这32个pairs的情况进行学习,也就是分别求它们的Q函数值与各自的target方差(或者是别的误差函数),之后再求和,针对这个量进行梯度下降的更新操作。通过设置replay buffer有效降低了Q网络更新的频率,增强了学习的稳定性。
(2)target network
target network的设立是上述High-level idea的一个直接体现。在Q-Learning的过程中,我们通过梯度下降的方式让当前的Q函数(在当前状态-动作组合的Q函数值)趋近于target,以达到优化的目的,但是伴随着Q函数每次的更新,用于target计算的Q函数也随之变化,也就是计算target的“标准”也是一直在变化的,跟随Q函数的变化而变化。回顾一下target的计算过程,当不涉及terminal状态的时候,有
t a r g e t ( s ′ ) = R ( s , a , s ′ ) + γ max a ′ Q k ( s ′ , a ′ ) (1) target(s')=R(s,a,s')+\gamma \max_{a'}Q_k(s',a')\tag{1} target(s′)=R(s,a,s′)+γa′maxQk(s′,a′)(1)
我们通过greedy的方式计算target值,这和我们在训练当中选择action的策略(最新Q网络, ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略)不同,即这种做法是off-policy的。这里之所以说target是s’的函数,是由于在给定s,a的时候,由于下一个状态s‘仍然是不确定的,这就成了影响target的唯一因素,所以说s’是自变量。正如上边所描述的,每次更新Q网络之后都会影响target的计算方法,这种target变化过于频繁的情况同样不利于学习的稳定性。所以我们单独设置独立于Q网络之外的target network,作为降低target计算方法变化的手段。target network是Q网络的一个复制版本,但是其的更新频率慢于Q网络,也就是Q网络更新若干次后才更新一次target network,这样就可以使得学习过程中Q网络有更多机会逼近target,取得更好的学习效果。这种想法就高度类似于supervised learning。更进一步来说,如果不设置target network,设想一个场景,一个状态s在进行动作a之后获得了一个奖励,进入下一个状态s‘。如果状态空间是平滑的(smooth),那么通常情况下相邻的两个状态的差别(参数上的)不会太大,也就是s与s’高度相似。在这个transition当中由于获得了奖励,当从replay buffer中选到这个transition进行训练时,就会试图增大这个(s, a)组合的Q函数值,但是由于Q网络的generalize特性,实际上与s非常相近的状态s‘相关的Q函数值也很可能会增大,这就导致了一个后果,当再次遇到这个状态的时候, ϵ − g r e e d y p o l i c y \epsilon-greedy\ policy ϵ−greedy policy选择动作a会发现此时的target值更大了,而且和当前相比的距离和上次差不多,学习的结果就是进一步增大(s, a)。这个过程不断持续,最终造成的后果就是"chasing its own tail because of bootstrapping",Q网络的某些位置可能会得出无穷的结果,导致学习失败。因此target network的设置是十分必要的。
DQN的具体过程如左图所示,由于这个算法的重要性,在这里有必要对他的过程进行进一步的阐释。首先对replay buffer D D D进行初始化,注意D有大小限制N;然后对Q网络进行随机权重的初始化,并复制一份作为target网络的初始化。之后开始循环过程,每次循环的开头重新设定一个初始状态,随后进行T次的子循环处理,每次子循环中首先采用 ϵ − g r e d d y \epsilon-greddy ϵ−greddy策略进行action选择,确定状态-动作组合之后运行并获得奖励r和状态s‘,并将这个transition pair(s, a, r, s’)存入replay buffer。之后进行一次学习,在D中采样选出一定数量的transition作为minibatch进行学习,对选出的transition使用target network计算target值,之后采用误差函数计算误差,再进行梯度下降更新Q网络参数 θ \theta θ。其中,每进行C次的Q网络更新,就进行一次target网络的更新,将最新版本的Q网络复制到target网络当中。
注意到在上边叙述DQN算法的过程时,并没有直接说使用方差的方法计算Q函数值和target的误差,这是因为我们通常选择采用别的误差函数例如Huber loss function,以其增强学习过程的鲁棒性。另外,神经网络训练的优化算法选择也会对Q网络的训练效果产生巨大的影响,实际上这也是deep reinforcement learning的一个特点,神经网络训练的优化算法会对训练效果产生很大影响,通常会使用 A t o m Atom Atom或 R M S P r o p RMSProp RMSProp优化算法取代传统的 v a n i l l a S G D vanilla\ SGD vanilla SGD算法。另外, ϵ − g r e e d y \epsilon-greedy ϵ−greedy算法中 ϵ \epsilon ϵ算法的变化情况也应当加以注意,其的大小应该在第一阶段逐渐下降,在进行million量级次的训练过后,逐渐稳定在0.05到0.1左右的值。
我们通常会使用Atari平台上的游戏来测试RL算法,结合CNN的方法,已经取得了很好的效果。正如左图展示的那样,我们在一个名为Pong的游戏当中测试算法性能,可以看到不同局面下Q网络给出的值,可选的动作有no-op,up,down三种,在1号局面下虽然小球距离右侧的距离已经很近,但是网络判定现在的局面还可以不用急于作出反应;2号局面和1号局面很相近,但是形势更加“危急”一点,Q网络判定此时“up”这一action的Q函数值是正的,而另外两个都是负的,说明Q网络希望引导agent作出向上移动的决定,这和我们的认知是符合的。另外两个局面也可以一样解读,Q网络的预测和我们的认知基本相似,其效果相当可观。
三、Double DQN以及一些其他的改进
这一部分列举了几个对于DQN的改进,首先要解释一点,作者之所以把Double DQN着重强调并不是由于它相比于别的改进版本更为重要,完全是出于个人需要,因为作者目前正在使用的TD3算法(基于policy gradient算法,是DDPG的改进版本)借鉴了Double DQN的思路,因此在这里着重提一下便于之后使用。
(1)Double DQN
在(1)当中我们给出了计算target的方法,其中采用max函数选择s‘状态下当前Q函数值最大的动作进行target计算。事实上这种方法存在估计值过大的偏向性(upward bias),可能会导致最终Q网络的值偏高,影响正确决策。之前的DQN方法中采用target网络作为动作选择和评估的网络,也就是根据target网络Q函数值的大小评估s‘状态下各动作a’对应的(s’, a’)组合,选择最大的一个动作a‘【选择】,再直接使用刚刚用于评估的此a’的target网络Q值带入计算target【评估】。在double DQN算法中将选择和评估动作分开,选择时采用当前Q网络,评估的时候才采用target网络,即target计算是这样的
t a r g e t ( s ′ ) D D Q N = R ( s , a , s ′ ) + γ Q ^ k ( s ′ , a r g m a x a ′ ( Q k ( s ′ , a ′ ) ) ) (2) target(s')_{DDQN}=R(s,a,s')+\gamma \hat Q_k(s',argmax_{a'}(Q_k(s',a')))\tag{2} target(s′)DDQN=R(s,a,s′)+γQ^k(s′,argmaxa′(Qk(s′,a′)))(2)
通过这种方式,可以有效减小upward bias,获得更好的学习效果
(2)Prioritized Experience Replay
在replay buffer中存储着相当数量的transition,但是在DQN算法当中,每次学习时都是针对其随机采样,没有任何偏向性,但是不同transition的“学习价值”是不同的,有的transition可能Q函数值和target值差距很小,学习价值较低;相应的差别较大的transition学习价值较高,值得反复学习,因此Prioritized Experience Replay采用Bellman error ∣ R + γ m a x a Q ( s ′ , a ′ ) − Q ( s , a ) ∣ |R+\gamma max_aQ(s',a')-Q(s,a)| ∣R+γmaxaQ(s′,a′)−Q(s,a)∣来对transition赋予权重,使得采样时更有偏向性地选到值得反复学习的transition pairs,大大提高了学习效率。
(3)Dueling DQN
Dueling DQN将Q函数值进行分解,分解成value/advantege两个部分
Q π ( s , a ) = V π ( s ) + A π ( s , a ) (3) Q^\pi(s,a)=V^\pi(s)+A^\pi(s,a)\tag{3} Qπ(s,a)=Vπ(s)+Aπ(s,a)(3)

正如左图所示,相比于传统DQN,Dueling DQN的Q函数网络输出的不是单一的Q(s, a),而是V(s)和A(s, a)两部分,通过这种方法就可以奇迹般地提高学习效果。