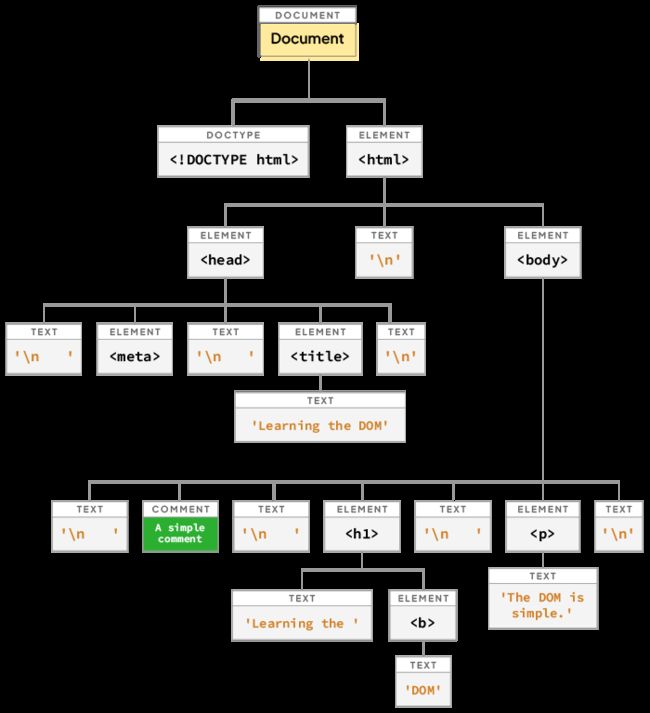
【数据结构与算法——TypeScript】树结构Tree
【数据结构与算法——TypeScript】
树结构(Tree)
认识树结构以及特性
什么是树?
真实的树:相信每个人对现实生活中的树都会非常熟悉
我们来看一下树有什么特点?
▫️ 树通常有一个根。连接着根的是树干。
▫️ 树干到上面之后会进行分叉成树枝,树枝还会分叉成更小的树枝。
▫️ 在树枝的最后是叶子。
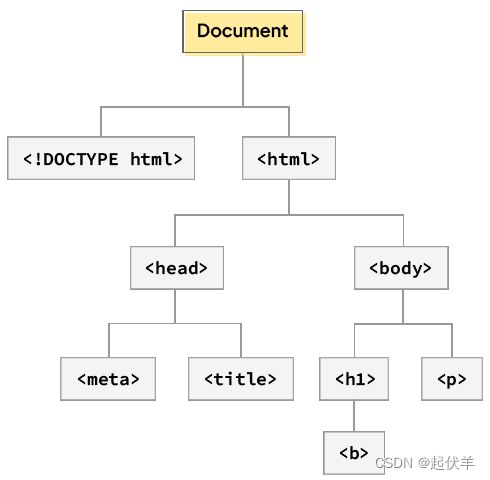
树的抽象:
专家们对树的结构进行了抽象,发现树可以模拟生活中的很多场景。
模拟树结构
树结构的抽象
❤️ 我们再将里面的数据移除,仅仅抽象出来结构,那么就是我们要学习的树结构

树结构的优点和术语
树结构的优点
我们之前已经学习了多种数据结构来保存数据,为什么要使用树结构来保存数据呢?
树结构和数组/链表/哈希表的对比有什么优点呢?
数组:
❤️ 优点:
- 数组的主要优点是根据下标值访问效率会很高。
- 但是如果我们希望根据元素来查找对应的位置呢?
- 比较好的方式是先对数组进行排序,再进行二分查找。
- 链表的插入和删除操作效率都很高。
缺点:
- 需要先对数组进行排序,生成有序数组,才能提高查找效率。
- 另外数组在插入和删除数据时,需要有大量的位移操作(插入到首位或者中间位置的时候),效率很低。
链表:
❤️ 优点:
- 链表的插入和删除操作效率都很高。
缺点:
- 查找效率很低,需要从头开始依次访问链表中的每个数据项,直到找到。
- 而且即使插入和删除操作效率很高,但是如果要插入和删除中间位置的数据,还是需要重头先找到对应的数据。
哈希表:
❤️ 优点:
- 我们学过哈希表后,已经发现了哈希表的插入/查询/删除效率都是非常高的。
- 但是哈希表也有很多缺点。。
缺点:
- 空间利用率不高,底层使用的是数组,并且某些单元是没有被利用的。
- 哈希表中的元素是无序的,不能按照固定的顺序来遍历哈希表中的元素。
- 不能快速的找出哈希表中的最大值或者最小值这些特殊的值。
树结构:
❤️ 优点:
- 我们不能说树结构比其他结构都要好,因为每种数据结构都有自己特定的应用场景。
- 但是树确实也综合了上面的数据结构的优点(当然优点不足于盖过其他数据结构,比如效率一般情况下没有哈希表高)。
- 并且也弥补了上面数据结构的缺点。。
而且为了模拟某些场景,我们使用树结构会更加方便。
- 因为数结构的非线性的,可以表示一对多的关系
- 比如文件的目录结构。
树的术语
-
在描述树的各个部分的时候有很多术语。
- 为了让介绍的内容更容易理解,需要知道一些树的术语。
- 不过大部分术语都与真实世界的树相关,或者和家庭关系相关(如父节点和子节点),所以它们比较容易理解。
-
❤️ 树(Tree):n(n≥0)个节点构成的有限集合。
- 当n=0时,称为空树;
-
对于任一棵非空树(n>0),它具备以下性质:
-
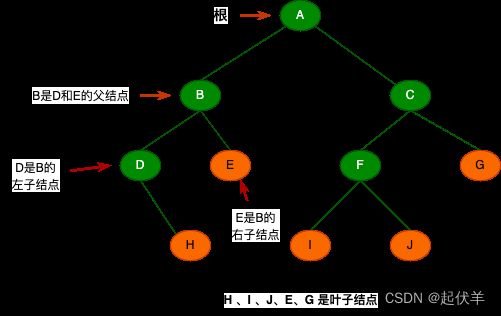
树的术语
- 节点的度(Degree):节点的子树个数。
- 树的度(Degree):树的所有节点中最大的度数。
- 叶节点(Leaf):度为0的节点。(也称为叶子节点)
- 父节点(Parent):有子树的节点是其子树的根节点的父节点
- 子节点(Child):若A节点是B节点的父节点,则称B节点是A节点的子节点;子节点也称孩子节点。
- 兄弟节点(Sibling):具有同一父节点的各节点彼此是兄弟节点。
- 路径和路径长度:从节点n1到nk的路径为一个节点序列n1,n2,nk
- ni是n(i+1)的父节点
- 路径所包含边的个数为路径的长度。
- 节点的层次(Level):规定根节点在1层,其它任一节点的层数是其父节点的层数加1。
- 树的深度(Depth):对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0。
- 树的高度(Height):对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0。

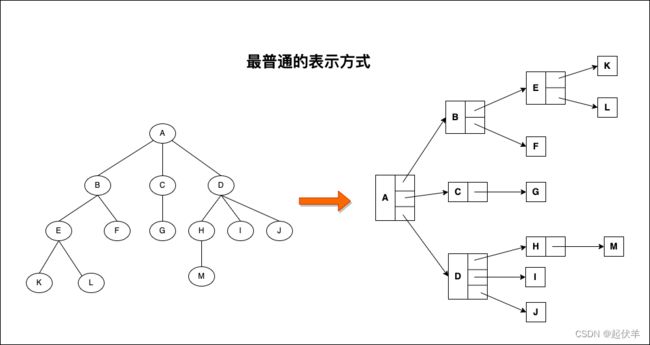
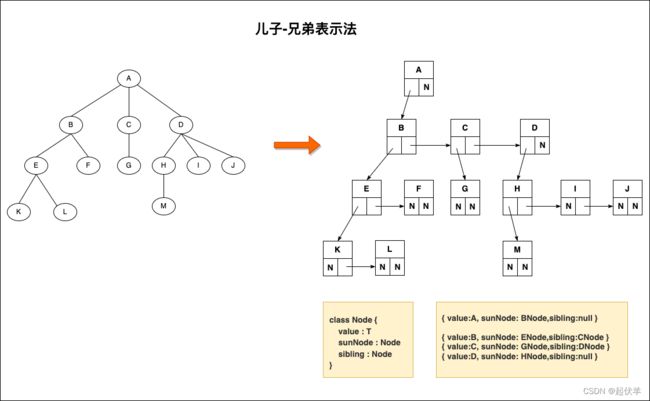
普通的表示方式
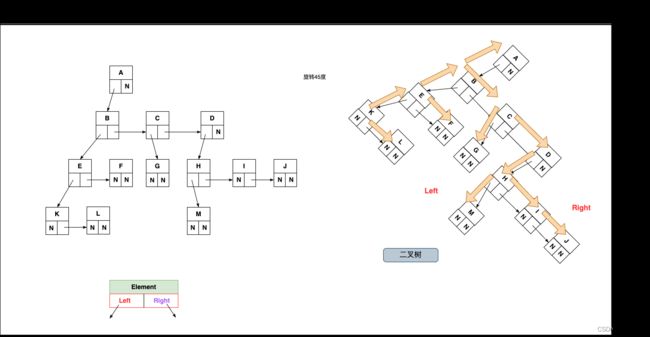
- 儿子-兄弟表示法旋转
- 其实所有树本质上都可以用二叉树模拟出来
二叉树特性以及概念
二叉树的概念
- 如果树中每个节点最多只能有两个子节点,这样的树就成为 “二叉树”。
- 前面,我们已经提过二叉树的重要性,不仅仅是因为简单,也因为几乎上所有的树都可以表示成二叉树的形式。
- 二叉树的定义
- 二叉树可以为空,也就是没有节点。
- 若不为空,则它是由根节点 和 称为其 左子树TL和 右子树TR 的两个不相交的二叉树组成。
- 二叉树有五种形态:
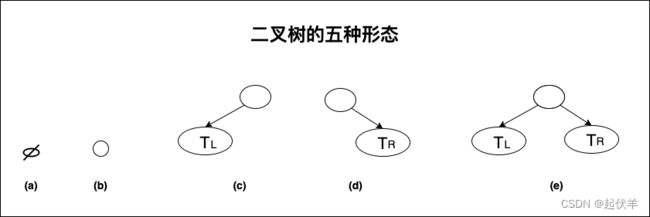
二叉树的特性
- 二叉树有几个比较重要的特性,在笔试题中比较常见:
- 一颗二叉树第 i 层的最大节点数为:2^(i-1),i >= 1;
- 深度为k的二叉树有最大节点总数为: 2^k - 1,k >= 1;
- 对任何非空二叉树T,若n0表示叶节点的个数、n2是度为2的非叶节点个数,那么两者满足关系 n0 = n2 + 1。
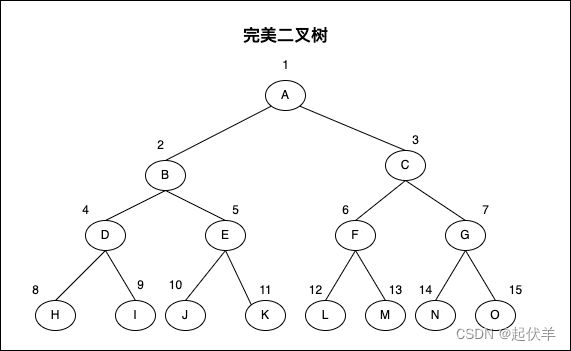
完美二叉树
- 完美二叉树(Perfect Binary Tree) ,也称为满二叉树(Full Binary Tree)
- 在二叉树中,除了最下一层的叶节点外,每层节点都有2个子节点,就构成了满二叉树。
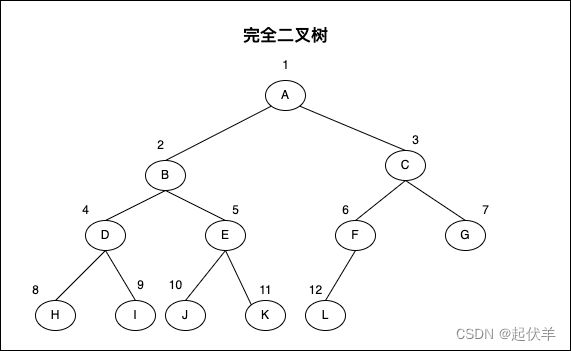
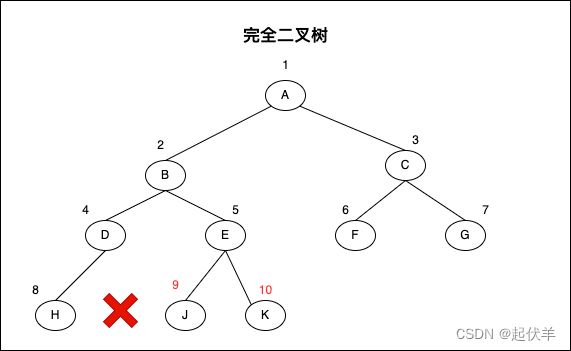
完全二叉树
-
完全二叉树(Complete Binary Tree)
- 除二叉树最后一层外,其他各层的节点数都达到最大个数。
- 且最后一层从左向右的叶节点连续存在,只缺右侧若干节点。
- 完美二叉树是特殊的完全二叉树。
-
下面不是完全二叉树,因为D节点还没有右节点,但是E节点就有了左右节点。
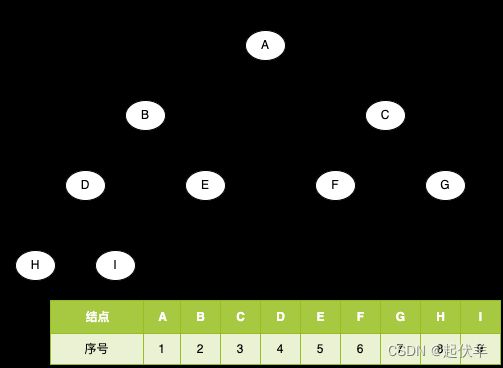
二叉树常见存储方式
二叉树的存储常见的方式是数组和链表
使用数组
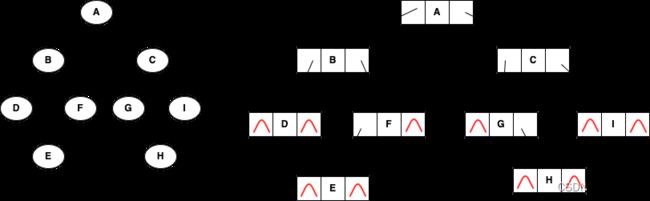
使用链表
认识二叉搜索树特性
什么是二叉搜索树?
-
二叉搜索树(BST,Binary Search Tree),也称 二叉排序树或 二叉查找树。
-
二叉搜索树是一颗二叉树,可以为空
-
如果部位空,满足以下性质:
-
- 非空左子树的所有键值小于其根节点的键值
-
- 非空右子树的所有键值大于其根节点的键值
-
- 左、右子树本身也都是二叉搜索树
-
-
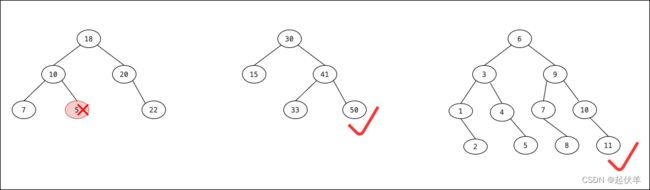
下面哪些是二叉搜索树,哪些不是?
-
二叉搜索树的特点:
- ✅ 二叉搜索树的特点就是相对 较小的值总是保存在左节点上,相对较大的值总是保存在 右节点上
- ✅ 查找效率高,这也是二叉搜索树中,搜索的来源
二叉搜索树
- ⭕️ 这种方式就是二分查找的思想:
- 查找所需的最大次数 等于 二叉搜索树的深度。
- 插入节点时,也 利用类似的方法,一层层比较大小,找到新节点合适的位置。
二叉搜索树类的封装
-
先封装一个BSTree的类
-
代码解析
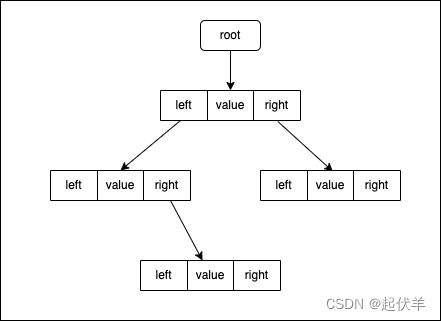
- 封装一个BSTree的类
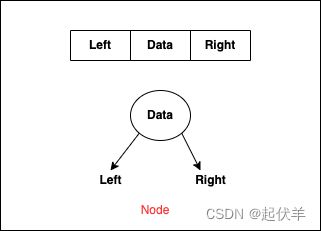
- 还需要封装一个用于保存每一个节点的类 Node
- 该类包含三个属性:节点对应的value、指向的左子节点树left、指向的右子节点树right
- 对于BSTree来说,只需要保存根节点即可,因为其他节点都可以通过根节点找到
-
代码
import { Node } from '../types/INode';
class IBSTreeNode<T> extends Node<T> {
left: IBSTreeNode<T> | null = null;
right: IBSTreeNode<T> | null = null;
}
class BSTree<T> {
root: IBSTreeNode<T> | null = null;
}
export {};
export class Node<T> {
value: T;
constructor(value: T) {
this.value = value;
}
}
二叉搜索树插入操作
- 二叉搜索树常见操作
1. 插入操作
insert (value):向树中插入一个新的数据。
2. 查找操作
search (value):在树中查找一个数据,如果节点存在,则返回true;如果不存在,则返回false 。
min:返回树中最小的值/数据。
max:返回树中最大的值/数据。
3. 遍历操作
inOrderTraverse :通过中序遍历方式遍历所有节点。
preOrderTraverse :通过先序遍历方式遍历所有节点。
postOrderTraverse :通过后序遍历方式遍历所有节点。
levelOrderTraverse :通过层序遍历方式遍历所有节点。
4. 删除操作(有一点点复杂)
remove (value):从树中移除某个数据。
向树中插入数据:分两部分
-
首先,外界调用的
insert方法- 代码解析:
- 首先,根据传入的
value,创建对应的Node。 - 其次,向树中插入数据需要分成两种情况:
- 第一次插入,直接修改根节点即可。
- 其他次插入,需要进行相关的比较决定插入的位置。
- 在代码中的
insertNode方法,我们还没有实现,也是我们接下来要完成的任务。
- 首先,根据传入的
- 代码解析:
-
其次,插入非根节点
- 代码解析:
- 插入其他节点时,我们需要判断该值到底是插入到左边还是插入到右边。
- 判断的依据来自于新节点的value 和原来节点的value值的比较。
- 如果新节点的newvalue 小于原节点的oldvalue ,那么就向左边插入。
- 如果新节点的newvalue 大于原节点的oldvalue ,那么就向右边插入。
- 代码的1序号位置,就是准备向左子树插入数据。但是它本身又分成两种情况
- 情况一(代码1.1位置):左子树上原来没有内容,那么直接插入即可。
- 情况二(代码1.2位置):左子树上已经有了内容,那么就一次向下继续查找新的走向,所以使用递归调用即可。
- 代码的2序号位置,和1序号位置几乎逻辑是相同的,只是是向右去查找。
- 情况一(代码2.1位置):左右树上原来没有内容,那么直接插入即可。
- 情况二(代码2.2位置):右子树上已经有了内容,那么就一次向下继续查找新的走向,所以使用递归调用即可。
- 代码解析:
-
代码:
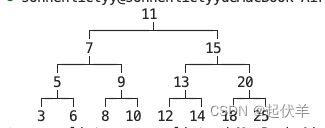
// 插入 private insertNode(node: BSTreeNode<T>, newNode: BSTreeNode<T>) { if (newNode.value < node.value) { // 在左子树节点插入 : 查找空白位置 if (node.left === null) { node.left = newNode; } else { this.insertNode(node.left, newNode); } } else { // 在右子节点查找空白位置 if (node.right === null) { node.right = newNode; } else { this.insertNode(node.right, newNode); } } } insert(value: T): boolean { // 1. 根据value创建TreeNode节点 const newNode = new BSTreeNode(value); // 2. 判断是否有根节点 if (!this.root) { //当前树为空 this.root = newNode; } else { // 递归 this.insertNode(this.root, newNode); } return false; }// 打印树结构 import { btPrint } from 'hy-algokit'; // 打印树结构 print() { btPrint(this.root); }// 测试代码 const bst = new BSTree<number>(); bst.insert(11); bst.insert(7); bst.insert(15); bst.insert(5); bst.insert(3); bst.insert(9); bst.insert(8); bst.insert(10); bst.insert(13); bst.insert(12); bst.insert(14); bst.insert(20); bst.insert(18); bst.insert(25); bst.insert(6); bst.print();
遍历二叉搜索树
前面,我们向树中插入了很多的数据,为了能很多的看到测试结果。我们先来学习一下树的遍历。
- ❗️ 注意:这里我们学习的树的遍历,针对所有的二叉树都是适用的,不仅仅是二叉搜索树。
- ❤️ 树的遍历:
- 遍历一棵树是指访问树的每个节点(也可以对每个节点进行某些操作,我们这里就是简单的打印)
- 但是树和线性结构不太一样,线性结构我们通常按照从前到后的顺序遍历,但是树呢?
- 应该从树的顶端还是底端开始呢? 从左开始还是从右开始呢?
- 二叉树的遍历常见的有四种方式:
- 先序遍历
- 中序遍历
- 后序遍历
- 层序遍历
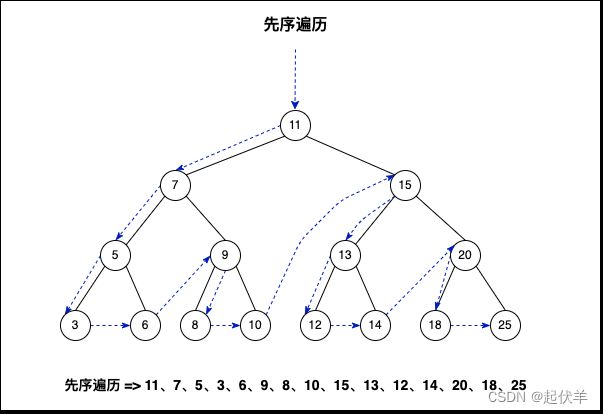
先序遍历 preOrderTraverse
- 遍历过程为:
- 优先访问根节点;
- 之后访问其左子树;
- 再访问其右子树。
private preOrderTraverseNode(node: BSTreeNode<T> | null) {
if (node) {
console.log(node.value);
this.preOrderTraverseNode(node.left);
this.preOrderTraverseNode(node.right);
}
}
preOrderTraverse() {
this.preOrderTraverseNode(this.root);
}
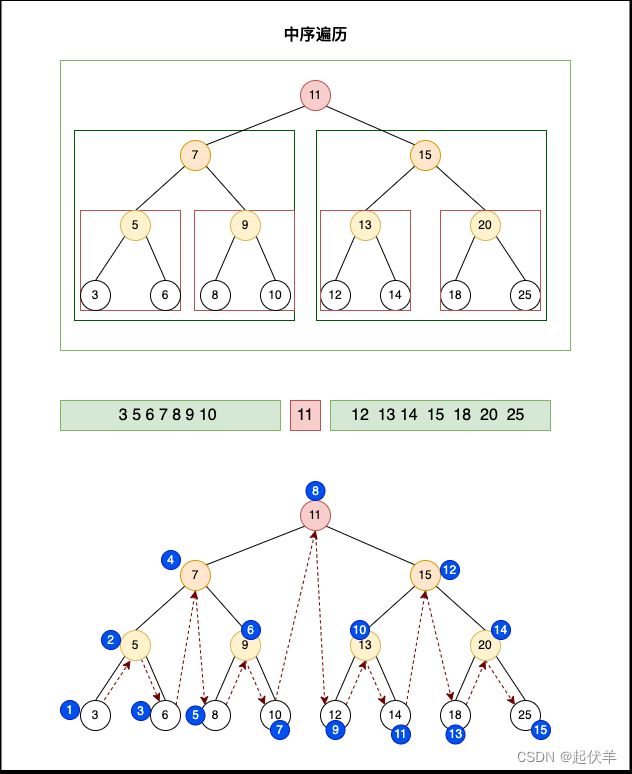
中序遍历 inOrderTraverse
- 遍历过程为:
- 中序遍历其左子树;
- 访问根节点;
- 中序遍历其右子树。
private inOrderTraverseNode(node: BSTreeNode<T> | null) {
if (node) {
this.inOrderTraverseNode(node.left);
console.log(node.value);
this.inOrderTraverseNode(node.right);
}
}
inOrderTraverse() {
this.inOrderTraverseNode(this.root);
}
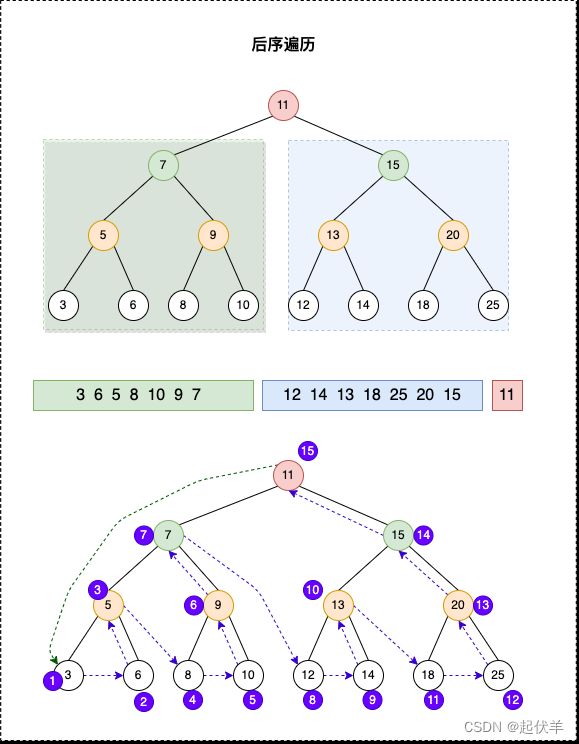
后序遍历 postOrderTraverse
- 遍历过程为:
- 后序遍历其左子树;
- 后序遍历其右子树;
- 访问根节点。
private postOrderTraverseNode(node: BSTreeNode<T> | null) {
if (node) {
this.postOrderTraverseNode(node.left);
this.postOrderTraverseNode(node.right);
console.log(node.value);
}
}
postOrderTraverse() {
this.postOrderTraverseNode(this.root);
}
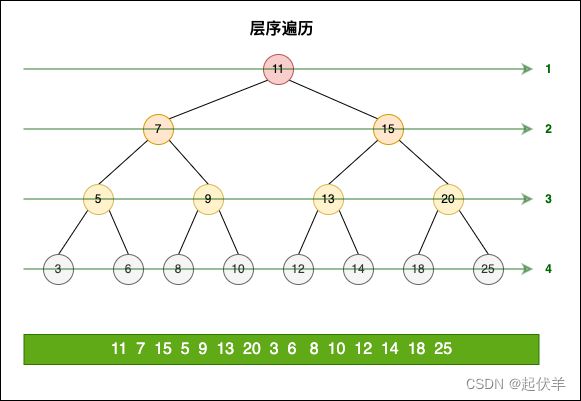
层序遍历 levelOrderTraverse
- 遍历过程为:
- 层序遍历很好理解,就是从上向下逐层遍历。
- 层序遍历通常我们会借助于队列来完成;
✓ 也是队列的一个经典应用场景;
- 代码分析
- 使用队列 : 遍历整个队列
- 访问队列中的出队元素
- 将出队的节点的左子节点和右子节点分别加入队列
levelOrderTraverse() {
// 1. 如果没有根节点,那么不需要遍历
if (!this.root) return;
// 2. 创建一个队列
const queue: BSTreeNode<T>[] = [];
// 队列中第一个节点是根节点
queue.push(this.root);
// 3. 遍历队列的长度
while (queue.length) {
// 弹出队列中当前元素
const current = queue.shift()!;
console.log(current.value);
// 将当前元素的左子节点和右子节点添加到队列
if (current.left) {
queue.push(current.left);
}
if (current.right) {
queue.push(current.right);
}
}
}
获取最大值和最小值
getMaxValue(): T | null {
let current = this.root;
while (current && current.right) {
current = current.right;
}
return current?.value ?? null;
}
getMinValue(): T | null {
let current = this.root;
while (current && current.left) {
current = current.left;
}
return current?.value ?? null;
}
search搜索特定的值
-
二叉搜索树不仅仅获取最值效率非常高,搜索特定的值效率也非常高。
- ❗️注意:这里的实现返回boolean类型即可。
-
代码解析:
- 这里我们还是使用了递归的方式。
- 递归必须有退出条件,我们这里是两种情况下退出。
- node === null,也就是后面不再有节点的时候。
- 找到对应的value,也就是node.value === value的时候。
- 在其他情况下,根据node.的value和传入的value进行比较来决定向左还是向右查找。
- 如果node.value > value,那么说明传入的值更小,需要向左查找。
- 如果node.value < value,那么说明传入的值更大,需要向右查找。
-
代码:
// 搜索特定值
private searchNode(node: BSTreeNode<T> | null, value: T): boolean {
// 如果node为空
if (node === null) return false;
// 判断node节点的value和value
if (node.value < value) {
return this.searchNode(node.right, value);
} else if (node.value > value) {
return this.searchNode(node.left, value);
} else {
return true;
}
}
search(value: T): boolean {
return this.searchNode(this.root, value);
}
二叉搜索树的删除
二叉搜索树的删除有些复杂,我们一点点完成。
-
删除节点要从查找要删的节点开始,找到节点后,需要考虑三种情况:
- 该节点是叶节点(没有字节点,比较简单)
- 该节点有一个子节点(也相对简单)
- 该节点有两个子节点.(情况比较复杂)
-
我们先从查找要删除的节点入手
- 先找到要删除的节点,如果没有找到,不需要删除
- 找到要删除节点
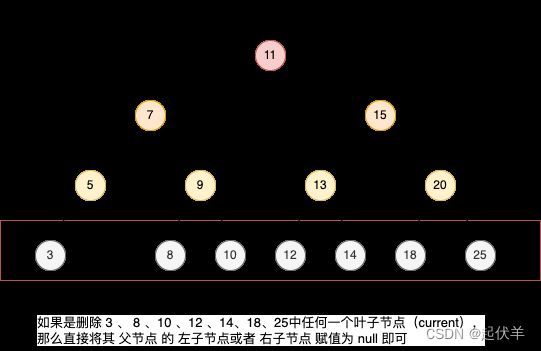
- 删除叶子节点
- 删除只有一个子节点的节点
- 删除有两个子节点的节点
-
代码分析:
- 搜索节点,节点是否存在
- 不存在,不需要任何操作
- 删除的节点是一个叶子结点
- 拿到当前叶子结点的父节点parent:判断是左子节点还是右子节点
- parent.left = null
- parent.right = null
- 删除的节点有一个子节点
- 删除的节点有两个子节点
- 搜索节点,节点是否存在
class BSTreeNode<T> extends Node<T> {
.
.
.
parent: BSTreeNode<T> | null = null;
get isLeft(): boolean {
return !!(this.parent && this.parent.left === this);
}
get isRight(): boolean {
return !!(this.parent && this.parent.right === this);
}
}
// 重构searchNode
private searchNode(value: T): BSTreeNode<T> | null {
let current = this.root;
let parent: BSTreeNode<T> | null = null;
while (current) {
// 如果找到current,直接返回
if (current.value === value) return current;
// 继续往下找
parent = current;
if (current.value < value) {
current = current.right;
} else {
current = current.left;
}
// 如果current有值,那么current保存自己的父节点
if (current) {
current.parent = parent;
}
}
return null;
}
remove(value: T): boolean {
// 1. 搜索:当前要删除的值
const current = this.searchNode(value);
// 1.1 节点不存在,不需要任何操作
if (!current) return false;
return true;
}
情况一:没有子节点
-
情况一:没有子节点
- 这种情况相对比较简单,我们需要检测current的left以及right是否都为null.
- 都为null之后还要检测一个东西,就是是否current就是根,都为null,并且为跟根,那么相当于要清空二叉树(当然,只是清空了根,因为只有它).
- 否则就把父节点的left或者right字段设置为null即可.
-
如果只有一个单独的根,直接删除即可
-
如果是叶节点,那么处理方式如下:
remove(value: T): boolean {
// 2.获取三个元素:当前节点、当前节点父节点、是属于左子节点/右子节点
// console.log('当前节点:', current.value, '当前节点父节点:', current.parent?.value);
// 2. 删除的节点是一个叶子结点
if (current.left === null && current.right === null) {
if (current === this.root) {
// 如果只有一个单独的根,直接删除即可
this.root = null;
} else if (current.isLeft) {
// 父节点的左子节点
current.parent!.left = null;
} else {
current.parent!.right = null;
}
return true;
}
return true;
}
情况二:有一个子节点
- 情况二:有一个子节点
- 要删除的current节点,只有2个连接(如果有两个子节点,就是三个连接了),一个连接父节点,一个连接唯一的子节点.
- 需要从这三者之间:爷爷 - 自己 - 儿子,将自己(current)剪短,让爷爷直接连接儿子即可.
- 这个过程要求改变父节点的left或者right,指向要删除节点的子节点.
- 当然,在这个过程中还要考虑是否current就是根.
- 分析:
- 如果是根的情况,比较简单.
- 如果不是根,并且只有一个子节点的情况.
remove(value: T): boolean {
// 3. 有一个子节点
// 3.1 只有左子节点
else if (current.right === null) {
if (current === this.root) {
this.root = current.left;
} else if (current.isLeft) {
current.parent!.left = current.left;
} else {
current.parent!.right = current.left;
}
}
// 3.2 只有右子节点
else if (current.left === null) {
if (current === this.root) {
this.root = current.right;
} else if (current.isLeft) {
current.parent!.left = current.right;
} else {
current.parent!.right = current.right;
}
}
return true;
}
情况三:两个子节点
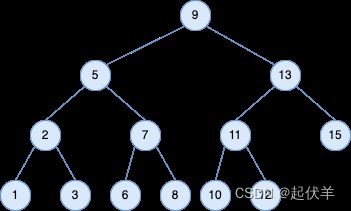
看下面的集中情况你怎么处理?
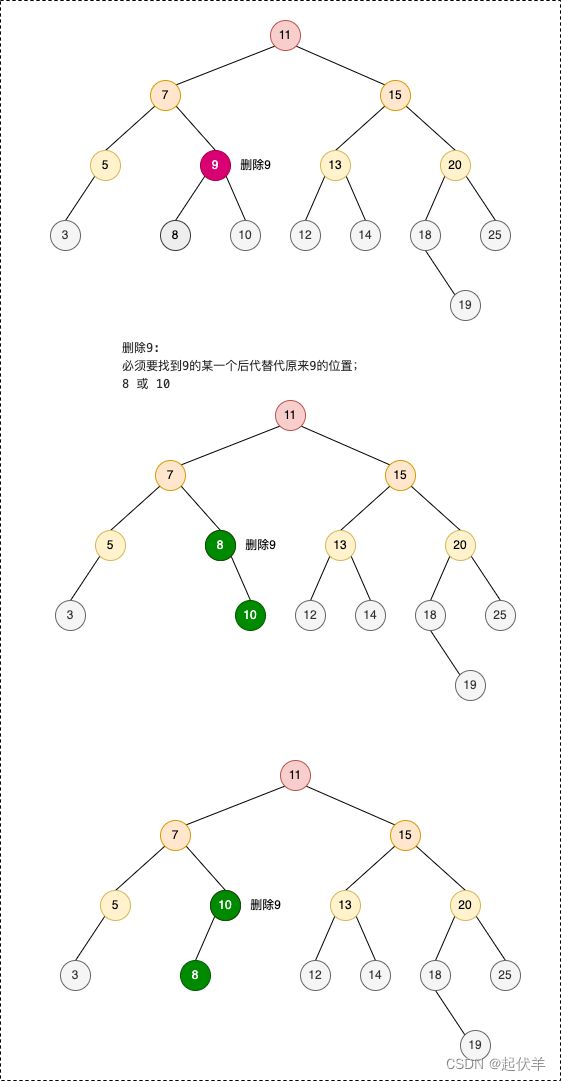
- 情况一:删除9节点
- 处理方式相对简单,将8位置替换到9,或者将10位置替换到9
- 注意:这里我说的是替换也就是8位置替换到9时7指向8,而8还需要指向10。
- 画图分析
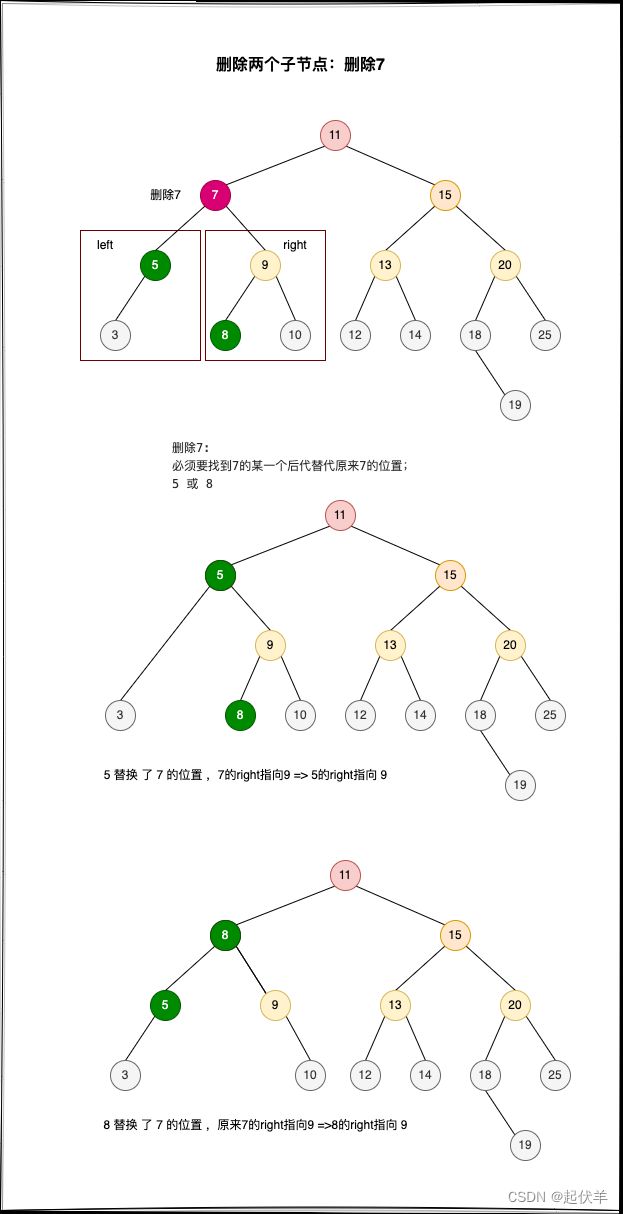
- 情况二:删除7节点
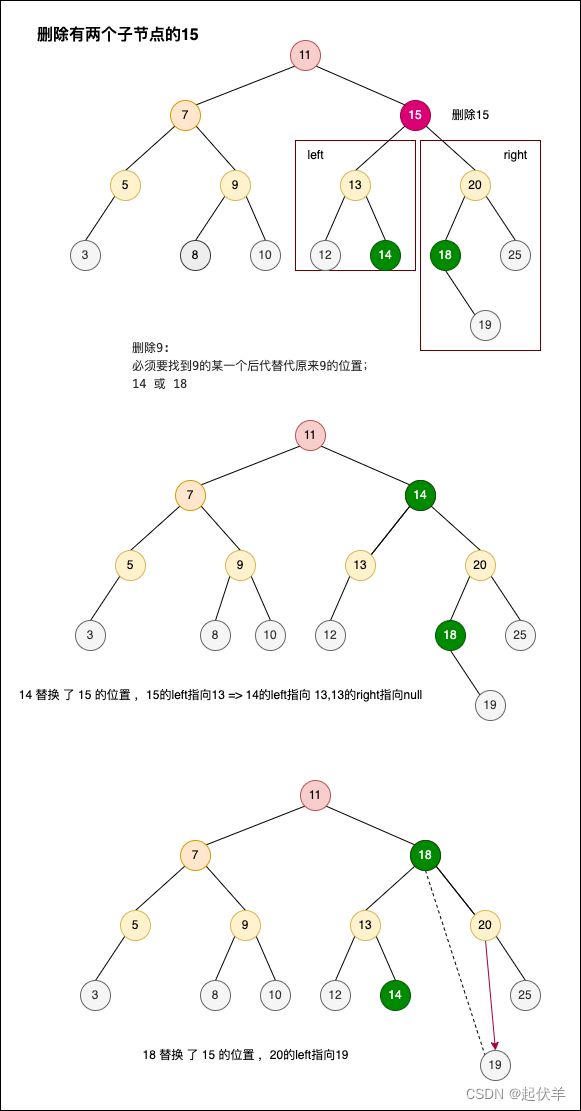
- 情况三:删除15节点,并且我希望也在右边找
寻找规律
如果我们要删除的节点有两个子节点,甚至子节点还有子节点,这种情况下我们需要从下面的子节点中找到一个节点,来替换当前的节点.
- 但是找到的这个节点有什么特征呢? ❤️ 应该是current节点下面所有节点中最接近current节点的.
- 要么比current节点小一点点,要么比current节点大一点点。
- 总结你最接近current,你就可以用来替换current的位置.
- ❤️ 这个节点怎么找呢?
- 比current小一点点的节点,一定是current左子树的最大值。
- 比current大一点点的节点,一定是current右子树的最小值。
- 前驱&后继
- 在二叉搜索树中,这两个特别的节点,有两个特别的名字。
- 比current小一点点的节点,称为current节点的前驱。
- 比current大一点点的节点,称为current节点的后继。
- 也就是为了能够删除有两个子节点的current,要么找到它的前驱,要么找到它的后继。
- 所以,接下来,我们先找到这样的节点(前驱或者后继都可以,我这里以找后继为例)
删除两个子节点代码
// 获取右子树
private getSuccessor(delNode: BSTreeNode<T>): BSTreeNode<T> {
// 获取右子树
let current = delNode.right;
let successor: BSTreeNode<T> | null = null;
while (current) {
successor = current;
current = current.left;
if (current) {
current.parent = successor;
}
}
// 如果拿到了后继节点
// console.log('删除节点:', delNode.value, '后继节点:', successor?.value);
if (successor !== delNode.right) {
successor!.parent!.left = successor!.right;
successor!.right = delNode.right;
}
//一定: 将删除节点的left,赋值给后继节点的left
successor!.left = delNode.left;
return successor!;
}
remove(value: T): boolean {
// 4. 有两个子节点
else {
const successor = this.getSuccessor(current);
if (current === this.root) {
this.root = successor;
} else if (current.isLeft) {
current.parent!.left = successor;
} else {
current.parent!.right = successor;
}
}
return true;
}
树的平衡性
- 为了能以较快的时间O(logN)来操作一棵树,我们需要保证树总是平衡的:
- 至少大部分是平衡的,那么时间复杂度也是接近O(logN)的
- 也就是说树中每个节点左边的子孙节点的个数,应该尽可能的等于右边的子孙节点的个数。
- 常见的平衡树有哪些呢?
- AVL树:
- AVL树是最早的一种平衡树。它有些办法保持树的平衡(每个节点多存储了一个额外的数据)
- 因为AVL树是平衡的,所以时间复杂度也是O(logN)。
- 但是,每次插入/删除操作相对于红黑树效率都不高,所以整体效率不如红黑树
- 红黑树:
- 红黑树也通过一些特性来保持树的平衡。
- 因为是平衡树,所以时间复杂度也是在O(logN)。
- 另外插入/删除等操作,红黑树的性能要优于AVL树,所以现在平衡树的应用基本都是红黑树。
- AVL树:
【数据结构与算法——TypeScript】 系列
1 、【数据结构与算法——TypeScript】数组、栈、队列、链表
2 、【数据结构与算法——TypeScript】算法的复杂度分析、 数组和链表的对比
3 、【数据结构与算法——TypeScript】哈希表