【学习笔记】A Gentle Introduction to Graph Neural Networks
Mask-guided BERT for Few Shot Text Classification
- 前言
- 什么是图
-
- Graphs and where to find them
-
- Images as graphs
- Text as graphs
- Graph-valued data in the wild
-
- Molecules as graphs
- Social networks as graphs
- Citation networks as graphs
- Other examples
- What types of problems have graph structured data?
-
- Graph-level task
- Node-level task
- Edge-level task
- The challenges of using graphs in machine learning
- 图神经网络
-
- The simplest GNN
- GNN Predictions by Pooling Information
- Passing messages between parts of the graph
- Learning edge representations
- Adding global representations
- 实验
-
- Some empirical GNN design lessons
- 相关技术
-
- Other types of graphs (multigraphs, hypergraphs, hypernodes, hierarchical graphs)
- Sampling Graphs and Batching in GNNs
- Inductive biases
- Comparing aggregation operations
- GCN as subgraph function approximators
- Edges and the Graph Dual
- Graph convolutions as matrix multiplications, and matrix multiplications as walks on a graph
- Graph Attention Networks
- Graph explanations and attributions
- Generative modelling
- Final thoughts
- 阅读总结
blog: https://distill.pub/2021/gnn-intro/
前言
图无处不在,一系列对象的连接组合,可以自然表示为图。研究者已经针对图数据构建神经网络,并取得了很好的效果。现在的研究者已经在探索如何将图应用到实际的场景中,如药物发现、物理模拟、交通预测等。
本文分为四个部分:
- 什么样的数据可以用来建模成图。
- 为什么图和其它数据类型不同。
- GNN网络的结构。
- GNN playground。
一个图由节点和关系组成,此外还包含全局的属性,如下图所示:
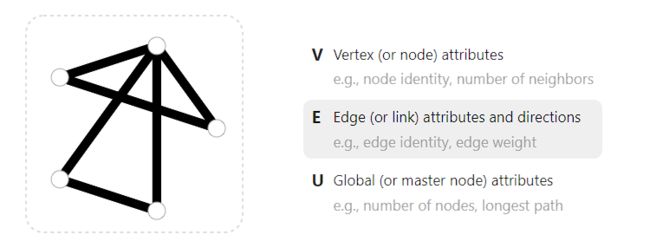
为了进一步描述每个节点、边或者整个图,我们可以把信息存储到图中的每个部分中。
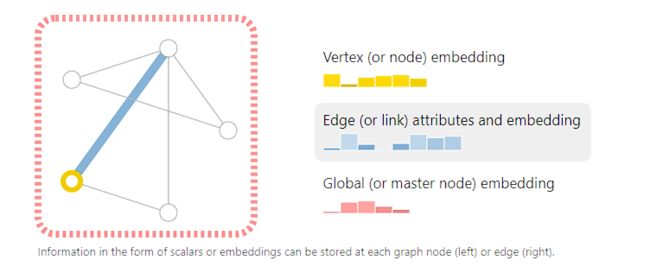
以上图为例,节点embedding维度,6,边embedding维度为8,全局embedding维度为5,这些表征信息都可以通过GNN学习得到。

从方向来说,图又可以分为有向图和无向图,比如微信好友关系就是无向图,而关注关系就是有向图。
什么是图
Graphs and where to find them
图是一种非常强大且通用的数据表示,甚至可以表示文本和图像。通过建模成图的形式,可以帮助我们了解其结构等特性。
Images as graphs
可以将图像中的每个像素点作为节点,通过边缘连接到相邻的像素,每个非边界像素正好有8个邻居,存储在每个节点的信息是三维RGB向量。
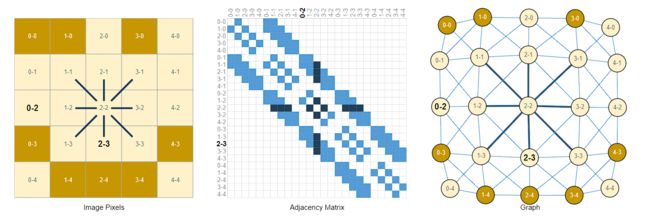
邻接矩阵可以可视化节点之间的连接情况,如上图中间所示。
Text as graphs
我们可以通过将索引关联到每个token,将文本表示为索引的序列,从而将文本数字化。这可以创建一个简单的有向图。

当然,这些文本和图像信息的图表示过于冗余了,因为它们本身就有规则的表示形式。如果强行表示成图的信息,在邻接矩阵中,图就是对角的带状结构,而文本只是一条对角线。
Graph-valued data in the wild
对于异构数据,每个节点的邻居是可变的,如果不用图的形式将很难表示。
Molecules as graphs
分子是由原子和电子组成的三维空间,所有的粒子都在相互作用,原子之间会有共价键来维持稳定,不同原子对有不同的距离,这可以描述为一个图,原子作为节点,共价键作为边。
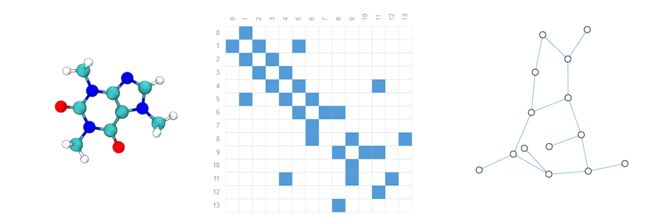
Social networks as graphs
社交网络是常见的图应用场景,可以利用图来表示不同人物之间的关系。
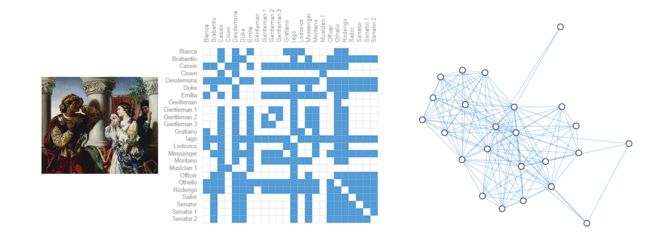
Citation networks as graphs
科学家之间的论文引用也可以建模成图,这是一种有向图的形式,每个节点可以将摘要信息嵌入到节点中。
Other examples
计算机视觉中的目标标签,机器学习建模,程序编码,数学公式等都可以建模成图的形式,其中变量是节点,边是将这些变量输入输出的操作。
What types of problems have graph structured data?
在图上,有三种常见的预测任务类型:
- 图级别:预测整个图
- 节点级别:预测图中节点的性质
- 边级别:预测边的性质
上面的任务都可以用GNN解决,下面对每个任务进行更细致的分析。
Graph-level task
图级别任务的目标是预测整个图的性质,例如,将分子表示为一张图,我们可能想要预测该分子有什么样的气味,或者是否能和与疾病相关的受体结合。

这种预测类似于分类任务。
Node-level task
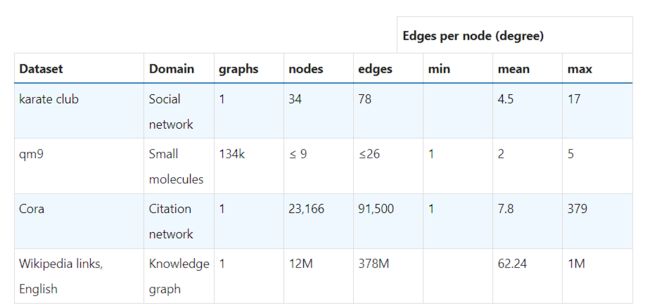
节点级别的任务关注于预测节点的身份或角色。一个经典的问题是扎克的空手道俱乐部。
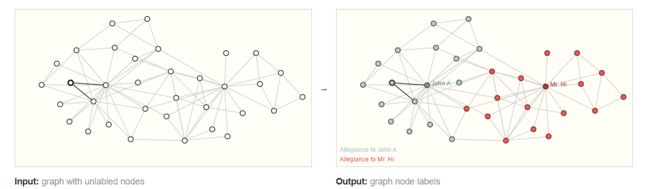
每个节点代表空手道练习者,边表示空手道成员之间的交互,由于管理员和教练产生分歧,空手道俱乐部分成两个流派,任务是预测每个空手道成员是忠于教练还是管理员。
Edge-level task
一个例子是图像场景理解。除了识别图像中的对象之外,深度学习模型还可以用于预测其中不同对象之间的关系。如预测下图中不同任务之间的动作关系。
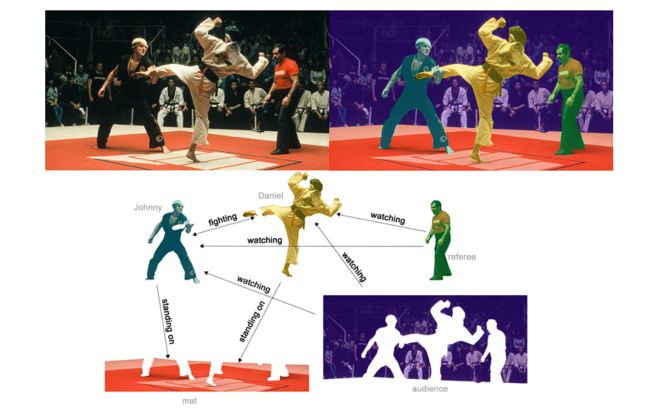
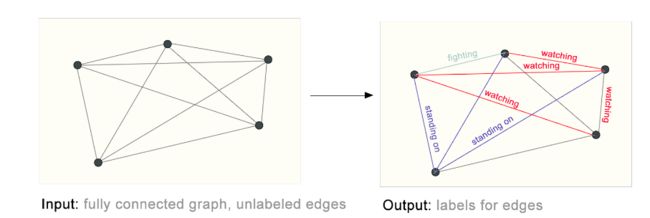
The challenges of using graphs in machine learning
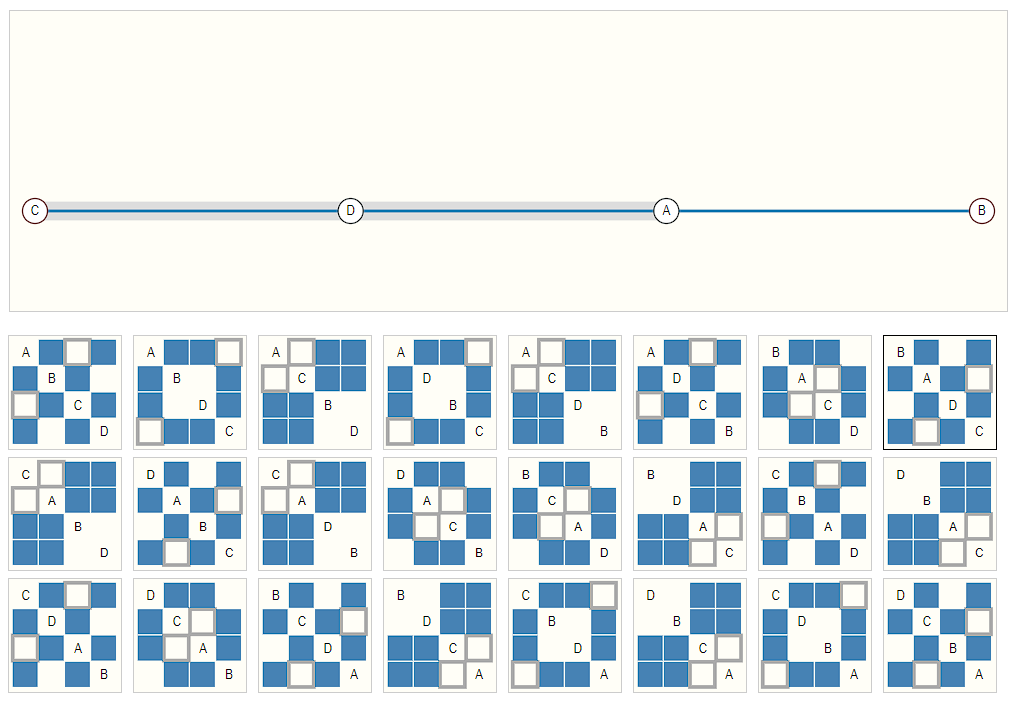
那么如何利用神经网络为这些图任务进行建模呢?第一步是要去思考我们如何将图与神经网络兼容。图中有四种信息:节点,边,全局信息和连接信息。前三者都可以直接建模为向量表征,但是图的连接信息表示更为复杂。连接矩阵虽然可以用于表示,但是由于其稀疏性,导致空间效率低下。此外,多个邻接矩阵可以表示同一个图,但是在神经网络中就会被认为是不同的表示。
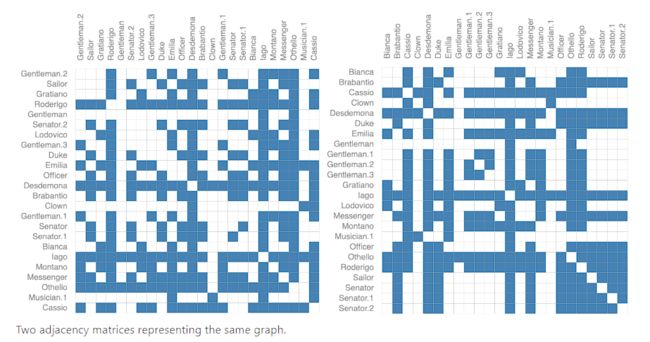
仅仅是四个节点,就可以得到24种不同的组合。
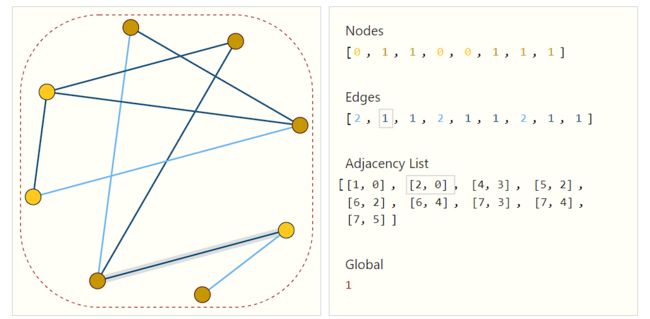
一种优雅的、节省内存的方法是邻接列表,只保存相相邻节点构成的tuple,如下图所示:
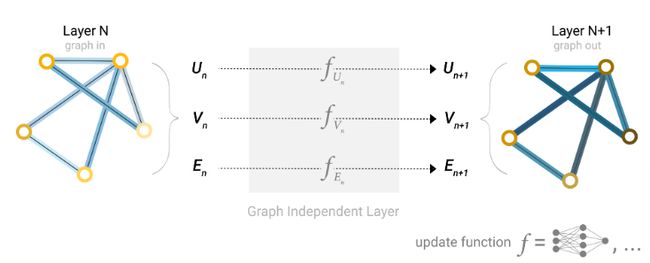
图神经网络
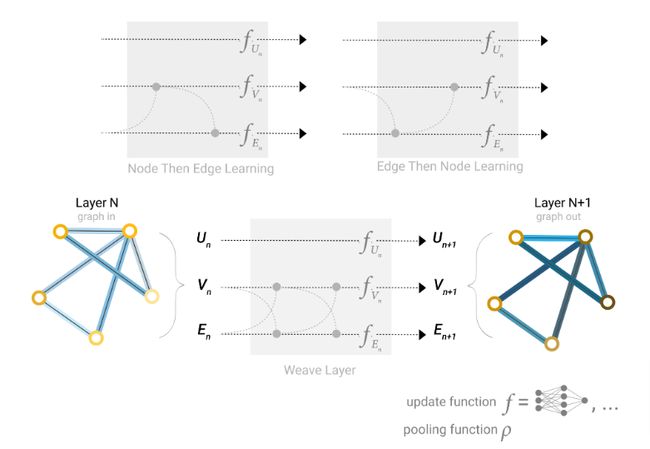
图的描述可以表示成排列不变的矩阵格式,因此可以采用图神经网络来解决图预测问题。GNN是对图的所有属性的可优化变换,它保持图的对称性(排列不变性)。采用信息传递神经网络框架构建GNNs。GNNs采用“图进、图出“结构,即输入是图的节点、边和全局信息,通过GNNs对这些embedding进行变换,输出时不改变图的结构。
The simplest GNN
最简单的GNN架构如上图所示,可以学习所有图属性的embedding,但是没有使用图中顶点的连接关系。GNN每一层可以理解为三个MLP,分别为节点、边和全局信息建模。
GNN Predictions by Pooling Information
既然已经构建好简单GNN模型,如何利用该模型执行预测任务呢?
以分类任务为例。如果任务的工作是预测节点,并且图中已经包含了节点的信息,直接对节点应用一个线性分类,即softmax输出得到预测结果的概率。
如果没有节点信息,只有边的信息,可以采用池化方法。分为两个步骤:
- 对于每个需要池化的item,将它们的embedding连接到一个矩阵中。
- 将聚合的embedding采取相加操作。

上图中相加的embedding,包括两个边和全局信息embedding三个item之间的相加。因此,如果我们只有边级特征,但是需要去预测节点的信息,可以采用池化操作将已知信息聚合起来。如下所示:
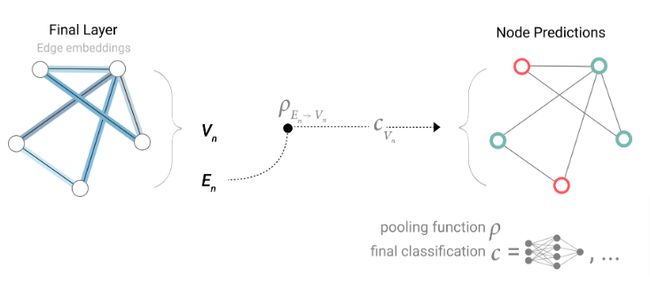
如果只有节点级别信息,需要去预测边的信息,模型将表示如下:
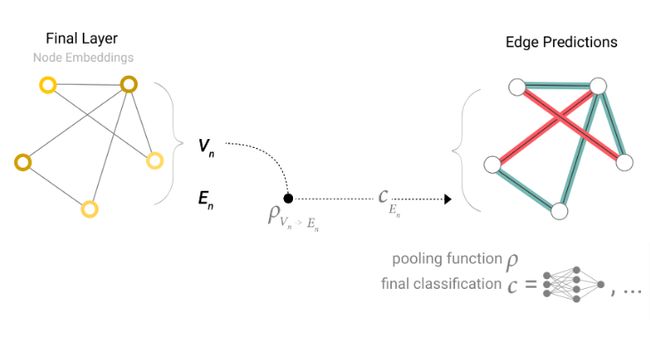
如果只有节点信息,需要去预测全局信息,只需要把所有节点的信息聚合起来,这一点有点像卷积神经网络中的Global Average Pooling层。同样的操作也适用于边信息。
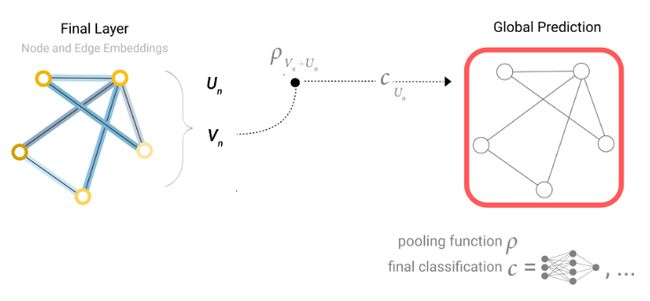
一个端到端使用GNN执行预测的过程如下:

只要有了池化技术,不管是什么属性,都可以通过类似的方法将信息传递过去。
Passing messages between parts of the graph
为了向GNN中引入图的连通信息,也可以采用信息传递的方式。其中,相邻的节点或者边交换各自的信息,并且影响其它节点或边的更新。
信息传递过程分为三步:
- 对于图中的每个节点,汇聚其所有邻居节点的表征信息。
- 通过聚合函数(如 add)聚合信息。
- 所有的池化信息经过更新函数传递,通常是一个可学习的神经网络。
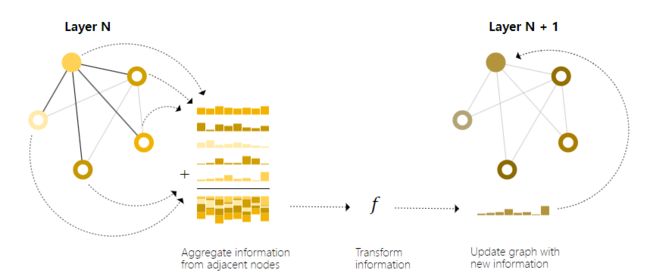
这样的操作和卷积有着异曲同工之妙。本质上,消息传递和卷积都是聚合和处理元素邻居信息的操作,以更新元素的值。在图中,元素是一个节点,在图像中,元素是一个像素,只不过图中的节点邻居是可变的,而图像中像素的邻居基本是固定数量的。
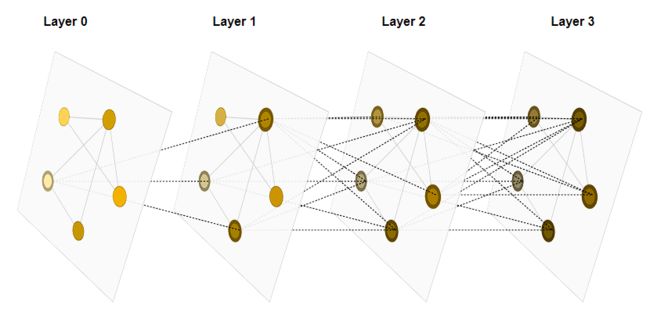
通过堆叠GNN层,一个节点最终可以汇聚图中所有的信息,如果是三层,那么就可以汇聚三步外节点的信息。
Learning edge representations
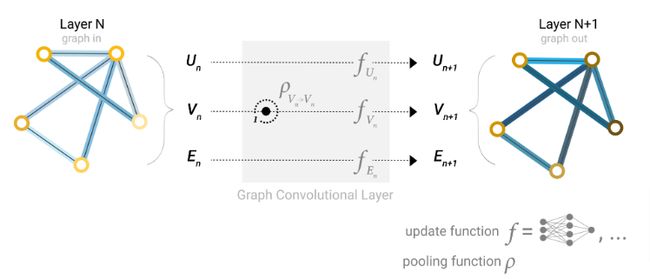
数据集并不是总能包含各个类型组件的信息,如果想要预测节点,但是只有边的信息,虽然上面已经介绍了使用池化技术来传递信息的方法,但是只是作用在模型的最后预测步骤,其实在GNN层中可以使用信息传递来共享信息,通过汇聚节点相邻边的信息对节点信息进行更新。由于边和节点信息的维度可能不同,可以通过学习一个线性的映射将边信息映射到节点信息。
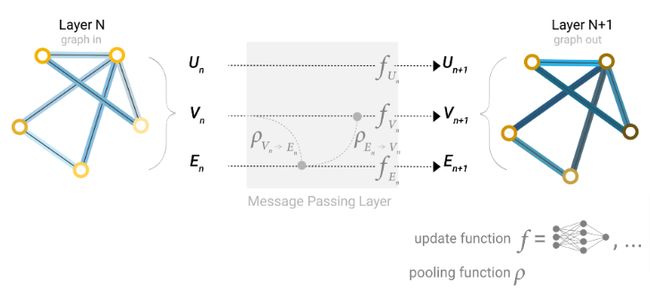
在构建GNN时,我们更新哪些图的属性以及以什么样的顺序去更新都是需要去考虑的。可以选择在边embedding之前更新节点embedding,也可以反过来,这是一个开放的策略。有四种更新的表示:
- 节点到节点
- 边到边
- 节点到边
- 边到节点
Adding global representations
到目前为止我们所描述的GNN网络还是有一定的缺陷,即距离较远的节点可能永远无法传递有效信息,这是受到GNN的层数影响。一种有效的方法是让所有节点能够互相传递信息,但是对于大型图来说,这样的方法成本过于高昂。
一种解决方法是全局表征,有时候又被称为master节点或者上下文向量。这个全局上下文向量连接网络中所有的节点和边,作为不同结点或边信息交换的桥梁,构建出图的全局表征。
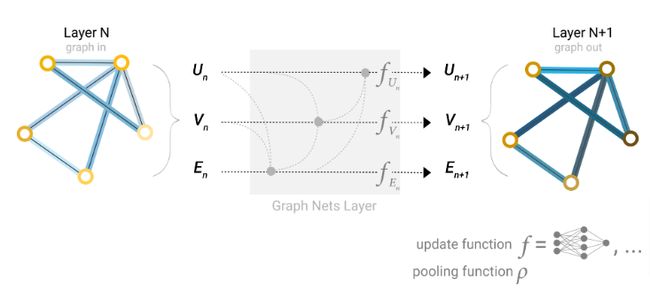
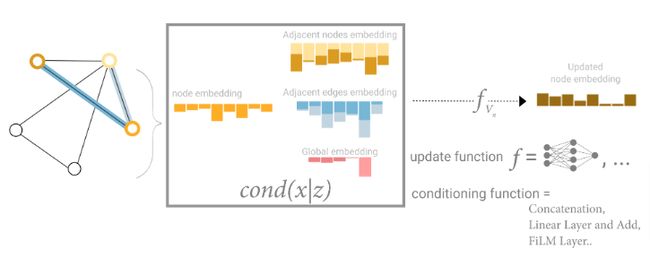
通过上面的描述,图中所有属性都可以学习到表征,因此在池化过程中,可以把我们认为有用的属性信息结合起来用于特定任务。结合可以是简单连接,也可以通过MLP进行映射。
实验
为了探索GNN中的组件如何工作,GNN playerground可以帮助读者通过在线调参,来理解每个部分的作用。使我们使用了关于不同气味分子的Leffingwell dor数据集,预测分子的结构是化学、物理等领域长久的难题。 为了简化问题,只考虑每个分子味道是否刺鼻,这是个二分类问题。每个分子都表示为图的形式,原子以one-hot形式代表是什么类型的元素。模型采用多层GNN,线性层输出最后的分类。可以改变的超参数如下:
- GNN的层数。
- 每个组件embedding的维度。
- 池化函数的类型:max,mean或者sum。
- 消息聚合的形式。
为了理解GNN是如何学习任务特定表征的,我们可视化了GNN倒数第二层激活函数的输出,并采用PCA降维,结果如下图右边所示。
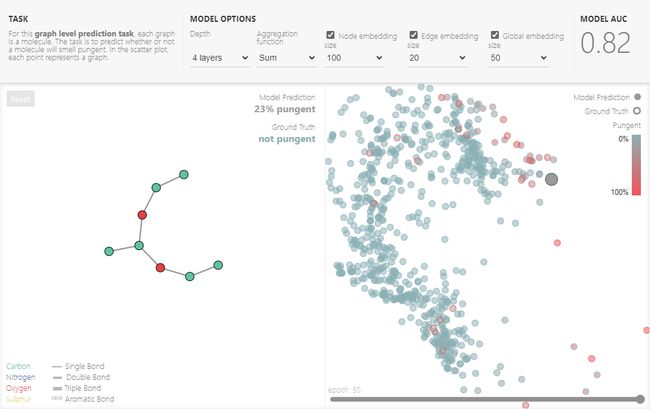
Some empirical GNN design lessons
本节探索什么样的设置会提升模型的性能。我们探索了信息传递的方式,embedding的维度,层数以及聚合函数类型。下图展示了模型性能随着可训练参数量(embedding维度)的变化结果:
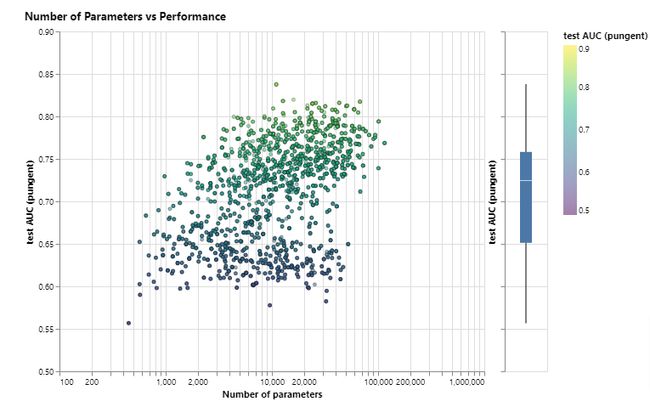
可以看出,可训练参数数量越多,性能呈现更好的趋势,但是即使参数量很小,也可以有很好的表现。具体到各个不同组件的embedding,又有如下的结果:
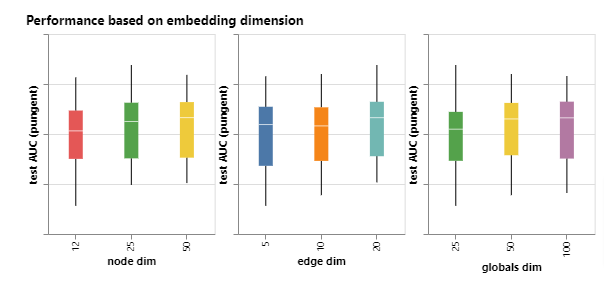
同样,具有更高维度的模型往往具有更好的均值和下界性能,但是在最大值上没有这样的趋势。接下对模型的层数进行分析:
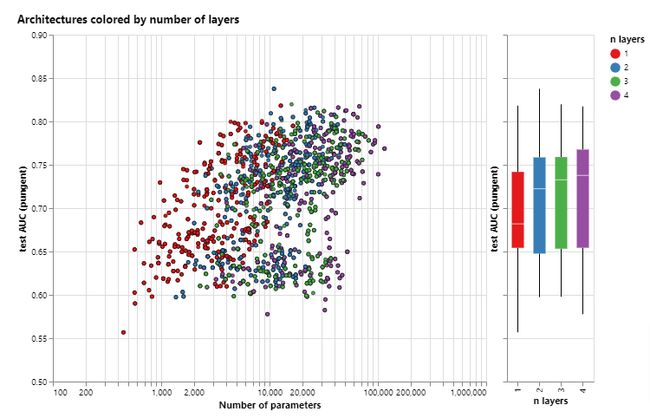
箱线图展现了类似的趋势,平均性能随着层数增加而增加。具有更高层数的GNN可以在更长的距离上广播其信息。
下图对聚合类型进行分析:
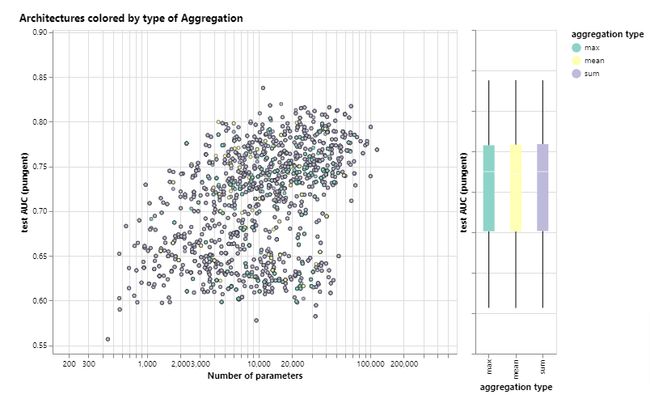
整体上来看,三种聚合类型都没有明显的差别。下面根据信息传递的方式对性能的影响进行分析。这里考虑了不传递信息、传递点信息、传递边信息和传递全局信息的模型。
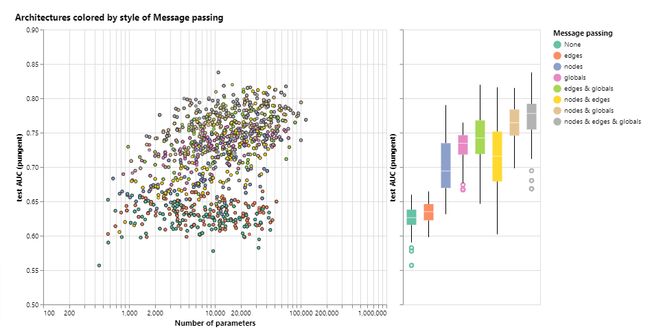
总的来说,随着信息传递的属性越多,模型性能越好,全局表示的信息可以显著提升性能,此外节点信息可能比边信息更有用,因为节点往往包含更多的信息。从这里出发可以有很多的方法来提高模型的表现,但是主要强调两个方向,一个是图算法的复杂度,另一个是图本身。
到目前所介绍的GNN,都是基于邻居池化操作,但是有很多图概念是无法通过这种方式表达的,例如线性图路径。设计新的机制在GNN中提取、执行和传播图是当前的研究方向。
GNN当前的前沿工作并不是建立新的模型和架构,而是如何构建图,具体来说,如何给图注入可以利用的额外结构或关系。正如上图所示,图属性交互越多,模型性能越好,可以考虑在节点中加入额外的空间关系,让图具有更丰富的特征。
相关技术
Other types of graphs (multigraphs, hypergraphs, hypernodes, hierarchical graphs)
上面只描述了每个属性向量化信息,实际上图的结构更灵活,可以包含其它类型的信息。幸运的是,消息传递框架非常灵活,通过定义新的图属性传递和更新信息可以帮助GNN适应更复杂的图结构。
比如,可以定义多边图或者嵌套图,如下所示:
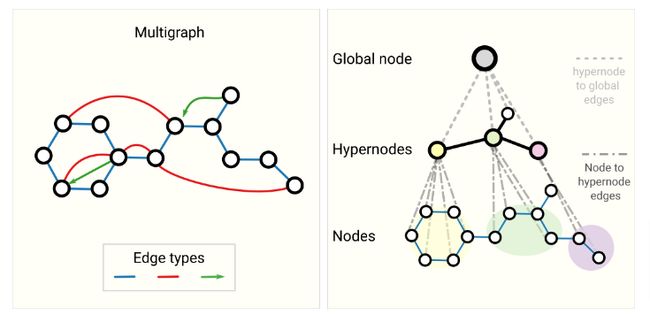
社交网络就可以定义成一种多边图,例如不同人之间的关系类型,嵌套图对表示分层的信息非常有用,比如考虑一个分子网络,一个GNN在化学反应上学习,一个GNN在分子水平上学习。
另一种类型的图是超图,其中一个边可以连接多个节点。
Sampling Graphs and Batching in GNNs
训练神经网络常见的方法是在随机采样的固定大小的批子图上进行梯度下降。对图进行批处理的主要思想是创建保留大图基本属性的子图,这种采样高度依赖上下文。如何采样一个图是一个开放的研究问题。有四种采样的方式:
- Random node sampling。随机采样均匀数量的节点,同时把这些节点k距离的所有节点和边采样出来。但是采样出来的节点个数不固定。
- Random walk sampling。随机游走,首先确定一个节点,从这个节点出发选取固定数量的节点。可以采样出固定的节点个数。
- Random walk with neighborhood。随机游走,并选取相邻k距离节点。
- Diffusion Sampling。选取一个点,将其k层近邻的点也采样出来。
当一个图的大小内存难以满足时,对图的采样就格外重要。
Inductive biases
当任务是解决特定数据类型上的问题时,我们希望构建特定模型能更好利用该数据类型的特征,这样往往能得到更好的性能。比如图像问题我们会采用卷积神经网络,因为它是平移不变的,所以不管图像中的狗在哪里,它都能预测出来。
在图的情况下,我们关心图中的节点、边和全局信息是如何关联的,图的模型应该保持图中实体之间的显式关系以及图的对称性(排列不变性)。在模型设计上,节点或边的操作顺序不重要,GNN对其作用是保持不变的。
Comparing aggregation operations
从邻居节点和边池化信息是任何功能强大GNN架构的重要步骤。由于每个节点的邻居是可变的,所以作者希望使用一种平滑的聚合操作,该操作与节点顺序和提供的节点数量保持不变。
常见的排列不变的操作包括sum、mean和max。
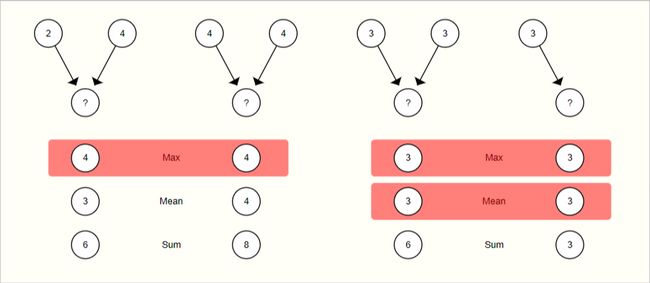
没有一种操作是最佳选择。当节点邻居数量变化很大时,mean操作很有效。当你想突出某个显著特征时,max操作很有效。sum相当于为这二者提供平衡。
GCN as subgraph function approximators
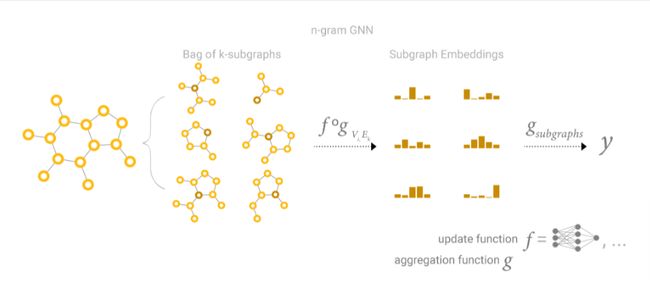
GCN可以看做是k个层、每层只看一个邻居节点的神经网络,该神经网络操作大小为k的子图的embedding。当只关注一个节点,经过k层后,更新的节点的表征包含了k距离范围内所有邻居节点的信息(类似于窗口大小为k的卷积层,但是卷积核权重相等),这个本质上来说是子图表示。边的表征也是同样的道理。
所以GCN是收集大小为k的所有可能的子图,并从一个节点或边的有利位置学习向量表示。可能的子图的数量可以组合增长,因此从一开始就枚举这些子图,而不是动态地构建它们。
Edges and the Graph Dual
点预测和边预测看起来不同,但是经常可以归结为同样的问题,在图上的变预测任务可以被建模为图上点预测的对偶。为了获得G的对偶,可以将节点转换为边(或者边转换为点),一个图和其对偶包含同样的信息,只是表示方式不同。有时候这样的转换可以更容易表示问题。
Graph convolutions as matrix multiplications, and matrix multiplications as walks on a graph
邻接矩阵和点特征矩阵的乘法使用求和方法实现简单的消息传递。需要注意的是,消息传递过程并不是更新节点的特征,而是汇聚邻居节点的特征。但是这很容易通过该MLP在矩阵乘法之前或之后传递特征。
从这一点可以看出邻接列表的好处,如果邻接矩阵稀疏,我们不需要将不连接的两个节点的0值也加进去。只要基于索引,就可以把所有连接的节点检索出。这种不需要矩阵乘法的方法使我们不必要将求和作为聚合操作。
可以想象,多次运用这种操作可以允许我们将信息传递更远,在这个意义上,矩阵的连乘是遍历图的一种方式。比如对于矩阵 A 2 A^2 A2,元素 A i j 2 A^2_{ij} Aij2统计了从节点 i i i到节点 j j j所有步长为2的遍历。
Graph Attention Networks
另一种传递图属性信息的方法是注意力机制。比如当我们考虑了节点和其1度距离的邻居节点的sum聚合时,可以采用加权和的方式。挑战在于如何以排列不变的方式将权重关联起来。一种方法是考虑一个标量评分函数,根据节点对分配权重。该评分函数的核心在于相邻节点和中心节点的关联程度,使用softmax函数将权重集中在任务相关的邻居节点上。从可解释性上分析,得分权重可以用于衡量边相对于特定任务的重要性。
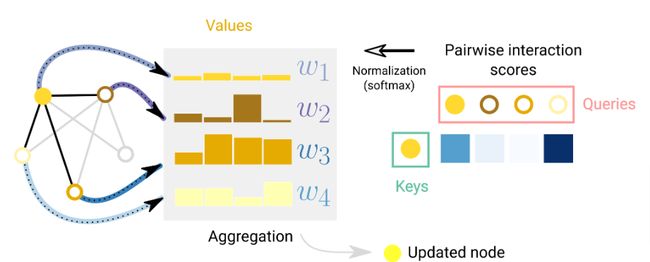
此外,Transformer可以被认为是具有attention机制的GNN。基于这个观点,Transformer模型把元素看做是全连接图的节点,注意力机制为每个节点对分配权重。Transformer和GNN的区别在于,前者是对所有连接进行建模,而后者是稀疏建模。
Graph explanations and attributions
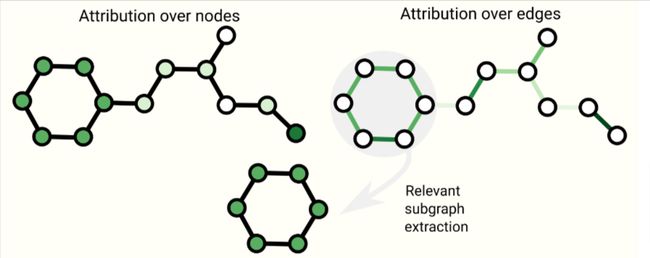
在部署GNN时,我们通常会关心模型的可解释性,以帮助调试模型或产生新的发现。我们发现在不同的上下文下,图的概念会有所不同。例如对于分子图,我们会关心子图的存在或缺失,对于引用图,我们会关系一篇文章的连接程度。由于图概念的多样性,有很多构建解释的方式。GNNExplain将这个问题转化为抽取对任务重要的相关子图。归因技术为图中重要部分分配排名。
Generative modelling
除了学习图上的预测模型,我们还可能关心图上的生成模型。生成模型是从学习分布中采样或给定图生成新图。一个相关的应用是在新药的设计中,需要特定性质的新分子作为治疗疾病的候选。一个挑战在于图的拓补结构,它的大小变化可以很大。一种解决方法是将邻接矩阵建模成带有自动编码器架构的图像。一个边是否存在可以看做是二分类任务。可以通过只预测已知节点之间不存在的边来解决 N n o d e s 2 N^2_{nodes} Nnodes2问题。graphVAE对邻接矩阵中的正连通模式和非连通模式进行建模。
另一种顺序构建图的方式是从图开始,迭代应用添加或删除节点和边的操作,可以采用强化学习policy gradient方法进行。
Final thoughts
图是一个强大丰富的数据类型,相对于文本和图像来说它具有不同的优势和挑战。本文介绍了基于图构建模型的发展历程。近几年GNNs的成功为大量新的问题出现创建了良好的机会,这些亟待研究人员去解决。
阅读总结
一篇GNNs基础性博客,让我了解了图数据类型的结构以及如何针对图这一数据类型进行建模,其中池化操作和信息聚合思想确实和很多经典模型结构如CNN、attention有异曲同工之妙。在我看来,对于任何数据类型,不管做什么样的任务,都需要充分利用好已有的知识,这就需要设计特定的模型来尽可能提取数据的信息。GNN模型的架构就是一种充分利用图类型数据的架构,它的思想无论是在实验效果还是在可解释性上都是独树一帜的。希望能够通过对图神经网络的学习,能够帮助我对NLP领域的研究有所启发。