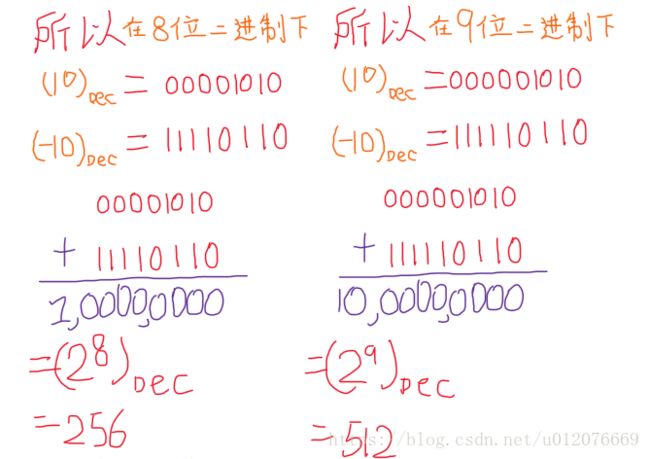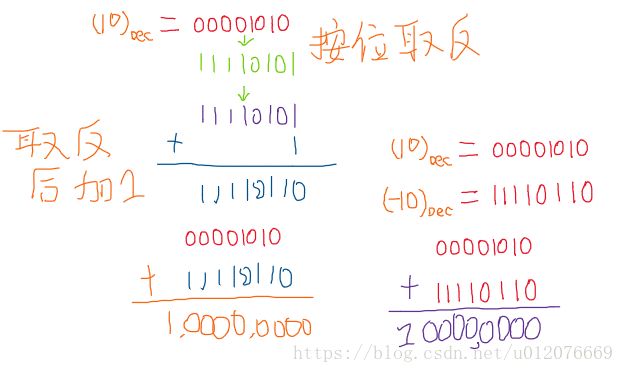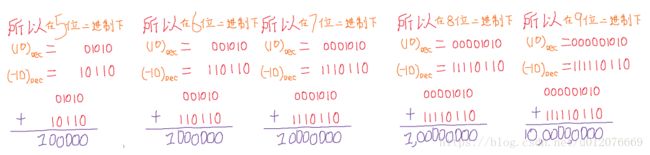微机原理与接口技术
/*符号扩展指令 CBW;CBW功能将AL中8位带符号数扩展为16位存入AX*/
/*C就是转换的意思,B指的是Byte,扩展到Word*/
符号扩展的总原则:
“有符号数在进行符号扩展(8位扩展到16位、16位扩展为32位等)时,正数(符号位为0)高位补0,负数(符号位为1)高位应补1,称为符号扩展。例如:
[00000001]补=[00000000 00000001]补 = 1
[11111111]补=[11111111 11111111]补 = -1”
——《微机原理与接口技术》周锋,倪晖编著
比如AL内容为86H,86H=1000,0110B
要把这个八位的数扩展到16位,那就应该在前面加八个1,而其数值不会变。
那么原理是什么呢?
首先,我们要介绍一下补码。
补码的由来:为了简化计算机ALU算术运算单元的操作,提高CPU的效率。
把ALU比作一个厨房的机械手,这个机械手有两个功能,一个是切菜,一个是炒菜。那么这个机械手在工作的时候,由于要在切菜和炒菜两个不同的任务中进行切换,工作效率(排除极端情况)理论上来说是不如两台机械手,一个负责切菜,一个负责炒菜的工作效率的。因为第一个机械手除了完成任务,还要耗费一定的时间在不同的任务场景之间进行切换。所以,要提高工作效率,最好是让一个机械手负责一个任务。
我们知道,数学有加法运算和减法运算。(乘法和除法暂不介绍)
人类计算加法或减法,是看式子中的符号是+还是-,
但是这个任务对计算机来说有点困难。
所以为了简化ALU的运算,最好就是让减法变成加法。
先插播一下原码的概念,一会会用到,原码就是十进制数转换为二进制数加上符号位(正数,符号位为0,负数,符号位为1),即:
怎么让减法变为加法呢?
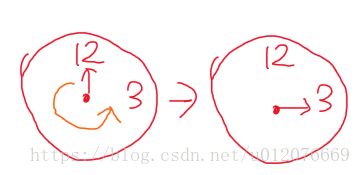
这里要讲到时钟的概念,你把时钟的时针顺时针推三格,和你把时钟的时针逆时针推九格得到的效果是一样的。
比如时针最初都指向十二,那么不管是哪个方法,都会让时针指向三。
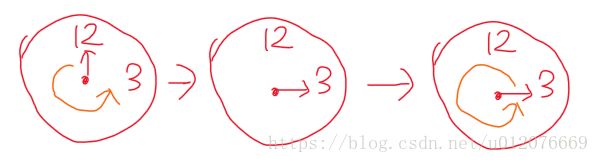
而且,不管你是
1.逆时针旋转9格,
2.顺时针旋转3格
3.或者你逆时针转了9格后,心情好,又逆时针转了12格,
不管是哪种情况,我们都会认为时针指向的是3,
在这种情况中,我们发现逆九和顺三都让时针指向3,且之后不管你逆还是顺了多少个12,结果还是3
所以总结,就是
把-9通过操作转换为正数,遵守的规则是
(-9+T)mod T
“与时钟类似,如果使用8位来表示有符号数,它的一周就是2的8次方=256,所以-1就可以用255(即2的8次方-1)来表示,这就是补码的含义”
给定一个数 -B,-B的补码是多少,必须先看它所处的周期是多少,用T表示周期的话,
T +(-B) 所得的值就是-B在周期T下的补码
例如,-9在周期256下所得的值为247,-9在周期65536下所得的值为65527
所以在周期256中,-9的补码为247;在周期65536中,-9的补码为65527
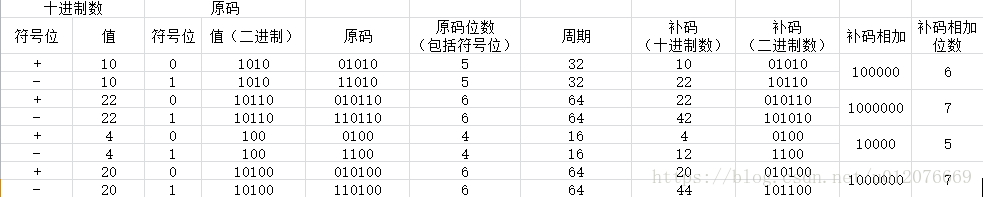
我们下面从几个例子中寻找一下规律
比较一下
发现一个有趣的现象:
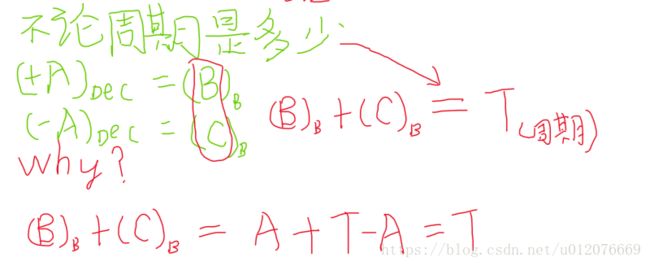
不论周期是多少,一个十进制正数A,与它的相反数-A,这两个数用周期转换成二进制数相加以后,结果一定为周期
比如这个表:
为什么会这样?因为这两个二进制数的运算转换成十进制不就是A+T-A吗,能不等于T吗,你说。
但是如果每次要算一个负数的补码都要先算通过刚才那一套手法:即用它加上周期,然后再进行转换。
这样子真是太麻烦了,首先不说你得先知道周期是多少,而且你还得进行转换(从十进制换成二进制),工作量巨大啊!
这个时候机智的人们发现了一个规律:
就是一个十进制数转成二进制后,与他的相反数转换成的二进制数相加,结果等于周期。
而通过另一种操作,也可以得到同样的结果:
两个方法对比发现,通过不同的操作,实现了相同的结果。
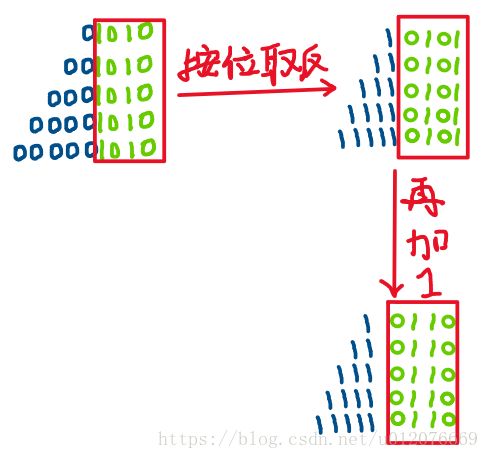
所以,通过将10的二进制数00001010按位取反得11110101后,再加1得11110110
这个11110110就是-10的补码。
概括:0和正数的补码就是本身,负数A的补码就是绝对值按位取反再加1.
恭喜你耐心地看到了这里,现在我们来进入正题,怎么对有符号数进行符号扩展:
同样还是从现象到规律
先观察现象:
机智的你应该发现其中的规律了吧,
如果是负数,要从原来的二进制位比如5位,扩展成9位的二进制数,怎么做?
在前面补1。
如果是正数,要从原来的二进制位比如5位,扩展成9位的二进制数,怎么做?
在前面补0。
为什么负数补1就可以呢?还是因为它的原码的特点来的。因为负数的补码就等于它的绝对值的二进制数按位取反加1,
-10的补码怎么求?首先你得告诉我你打算用几个二进制位来存储10这个数,(当然至少得是4个二进制位),
如果你要用5个二进制位存10,则10表示为01010,
如果你要用6个二进制位存10,则10表示为001010,
如果你要用7个二进制位存10,则10表示为0001010,
如果你要用8个二进制位存10,则10表示为00001010,
如果你要用79个二进制位存10,则10表示为000001010,
在上述五种情况下,用我们刚刚得到的求补码的办法:负数的补码就等于它的绝对值按位取反加1
来求-10的补码,
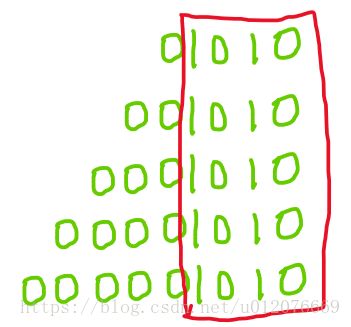
在上述五种情况中,对-10的绝对值的10的二进制为观察发现,最低的四位都是1010,而高位依次多了一个0
对共有部分1010按位取反的值都是一样的,都为0101,再加1,最低位结果也还是固定。
而剩余部分都为0,按位取反的值就都为1,
可不就是在前面补1 了吗。