【Sklearn】基于逻辑回归算法的数据分类预测（Excel可直接替换数据）)

1.模型原理

逻辑回归是一种用于二分类问题的统计学习方法，尽管名字中含有“回归”，但实际上是一种分类算法。它的基本原理是通过建立一个线性模型，然后将线性输出映射到一个概率值，最终将这个概率值转换成二分类的预测结果。

下面是逻辑回归的基本原理：

1. 线性模型： 首先，逻辑回归建立一个线性模型，将特征的线性组合映射到一个连续的实数范围。对于一个有n个特征的样本，线性模型可以表示为：
   $$z=b+w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n$$
   其中，$z$是线性组合的结果，$b$是偏差项（截距），$w_i$是特征的权重，$x_i$是对应的特征值。

2. Sigmoid函数（Logistic函数）： 为了将线性模型的输出转换成概率值，逻辑回归使用Sigmoid函数（也称为Logistic函数）来实现这个映射。Sigmoid函数将任意实数映射到0到1的区间，它的公式为：
   $$\sigma (z)=\frac{1}{1+e^{-z}}$$
   其中，$e$是自然对数的底数。

3. 概率预测： 经过Sigmoid函数映射后，$z$被转换成了一个0到1之间的概率值，表示样本属于正类的概率。对于二分类问题，通常将概率大于等于0.5的预测为正类，小于0.5的预测为负类。

4. 决策边界： 在训练过程中，逻辑回归通过调整权重$w_i$和偏差$b$来拟合训练数据。拟合的过程实际上是在找到一个适合的决策边界，将不同类别的样本分开。决策边界可以是一个超平面，使得在超平面上的点被分类为正类，超平面之外的点被分类为负类。

5. 损失函数和优化： 逻辑回归使用最大似然估计来确定参数，即找到能够使得观测数据出现的概率最大的参数。损失函数常用的是对数似然损失函数。模型通过优化算法（如梯度下降）来最小化损失函数，从而找到最佳的权重$w_i$和偏差$b$。

总之，逻辑回归通过线性模型和Sigmoid函数将特征映射到概率值，然后通过优化算法来调整模型参数，使得概率预测尽可能地与实际标签一致，从而实现对样本的分类预测。

2.模型参数

LogisticRegression类的构造函数允许你传递一系列参数来自定义模型的行为。你可以根据需要修改这些参数以优化模型的性能。以下是一些常用的参数及其说明：

1. penalty: 正则化项，可以是 “l1”、“l2”、“elasticnet” 或 “none”。默认是 “l2”。

2. C: 正则化强度的倒数，必须为正数。较小的值表示更强的正则化。默认为1.0。

3. solver: 优化算法，可以是 “newton-cg”、“lbfgs”、“liblinear”、“sag” 或 “saga”。默认是 “lbfgs”。

4. max_iter: 最大迭代次数，用于算法收敛。默认为100。

5. multi_class: 多分类问题的策略，可以是 “auto”、“ovr” 或 “multinomial”。默认是 “auto”。

6. random_state: 随机数生成器的种子，用于重现随机初始化。

7. class_weight: 类别权重，用于处理不平衡数据集。

8. tol: 收敛容忍度，用于控制算法停止的条件。

等等。

你可以在创建LogisticRegression对象时，通过参数传递来修改这些选项。例如：

from sklearn.linear_model import LogisticRegression

model = LogisticRegression(penalty='l1', C=0.1, solver='saga', max_iter=500)

在这个例子中，我们使用了不同于默认值的正则化方式、正则化强度、优化算法和最大迭代次数。

你可以根据自己的数据和任务需求来调整这些参数，以获得更好的模型性能。不同的参数组合可能会对模型的性能产生不同的影响，因此在选择参数时可以尝试不同的组合，并根据交叉验证等方法来选择最佳的参数设置。

3.文件结构

iris.xlsx						% 可替换数据集
Main.py							% 主函数

4.Excel数据

5.下载地址

- 资源下载地址

6.完整代码

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

def logistic_regression_classification(data_path, test_size=0.2, random_state=42):
    # 加载数据
    data = pd.read_excel(data_path)

    # 分割特征和标签
    X = data.iloc[:, :-1]  # 所有列除了最后一列
    y = data.iloc[:, -1]   # 最后一列

    # 划分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)

    # 创建逻辑回归模型
    # 1. ** penalty: ** 正则化项，可以是"l1"、"l2"、"elasticnet"或"none"。默认是"l2"。
    # 2. ** C: ** 正则化强度的倒数，必须为正数。较小的值表示更强的正则化。默认为1.0。
    # 3. ** solver: ** 优化算法，可以是"newton-cg"、"lbfgs"、"liblinear"、"sag"或"saga"。默认是"lbfgs"。
    # 4. ** max_iter: ** 最大迭代次数，用于算法收敛。默认为100。
    # 5. ** multi_class: ** 多分类问题的策略，可以是"auto"、"ovr"或"multinomial"。默认是"auto"。
    # 6. ** random_state: ** 随机数生成器的种子，用于重现随机初始化。
    # 7. ** class_weight: ** 类别权重，用于处理不平衡数据集。
    # 8. ** tol: ** 收敛容忍度，用于控制算法停止的条件。
    model = LogisticRegression(penalty='l1', C=0.1, solver='saga', max_iter=1000)

    # 在训练集上训练模型
    model.fit(X_train, y_train)

    # 在测试集上进行预测
    y_pred = model.predict(X_test)

    # 计算准确率
    accuracy = accuracy_score(y_test, y_pred)
    return confusion_matrix(y_test, y_pred), y_test.values, y_pred, accuracy

if __name__ == "__main__":
    # 使用函数进行分类任务
    data_path = "iris.xlsx"
    confusion_mat, true_labels, predicted_labels, accuracy = logistic_regression_classification(data_path)

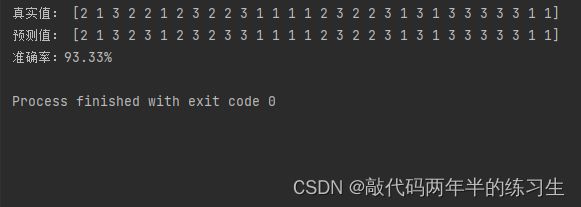
    print("真实值：",true_labels)
    print("预测值：", predicted_labels)
    print("准确率：{:.2%}".format(accuracy))

    # 绘制混淆矩阵
    plt.figure(figsize=(8, 6))
    sns.heatmap(confusion_mat, annot=True, fmt="d", cmap="Blues")
    plt.title("Confusion Matrix")
    plt.xlabel("Predicted Labels")
    plt.ylabel("True Labels")
    plt.show()

    # 用圆圈表示真实值，用叉叉表示预测值
    # 绘制真实值与预测值的对比结果
    plt.figure(figsize=(10, 6))
    plt.plot(true_labels, 'o', label="True Labels")
    plt.plot(predicted_labels, 'x', label="Predicted Labels")

    plt.title("True Labels vs Predicted Labels")
    plt.xlabel("Sample Index")
    plt.ylabel("Label")
    plt.legend()
    plt.show()

7.运行结果