LeetCode 399. 除法求值(中等)
399. 除法求值
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。
注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]
提示:
1 <= equations.length <= 20equations[i].length == 21 <= Ai.length, Bi.length <= 5values.length == equations.length0.0 < values[i] <= 20.01 <= queries.length <= 20queries[i].length == 21 <= Cj.length, Dj.length <= 5Ai, Bi, Cj, Dj由小写英文字母与数字组成
思路:这是一道没做出来的题。最开始的思路是最直接的打算给每个元素赋值,存储在map里,然后根据每个元素的值来计算最终结果,只通过了一半的样例。虽然看出了是有向图的问题,想到了拓扑排序和深度遍历,但是对这些数据结构和算法仅仅停留在了了解和认识的层面,还不会应用到代码里,因此最后还是参考了官方的题解。
学习别人的代码:
法一:并查集
作者:LeetCode
链接:https://leetcode-cn.com/problems/evaluate-division/solution/399-chu-fa-qiu-zhi-nan-du-zhong-deng-286-w45d/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
由于 变量之间的倍数关系具有传递性,处理有传递性关系的问题,可以使用「并查集」,我们需要在并查集的「合并」与「查询」操作中 维护这些变量之间的倍数关系。
可以将题目给出的 equation 中的两个变量所在的集合进行「合并」,同在一个集合中的两个变量就可以通过某种方式计算出它们的比值。具体来说,可以把 不同的变量的比值转换成为相同的变量的比值,这样在做除法的时候就可以消去相同的变量,然后再计算转换成相同变量以后的系数的比值,就是题目要求的结果。统一了比较的标准,可以以 O(1) 的时间复杂度完成计算。
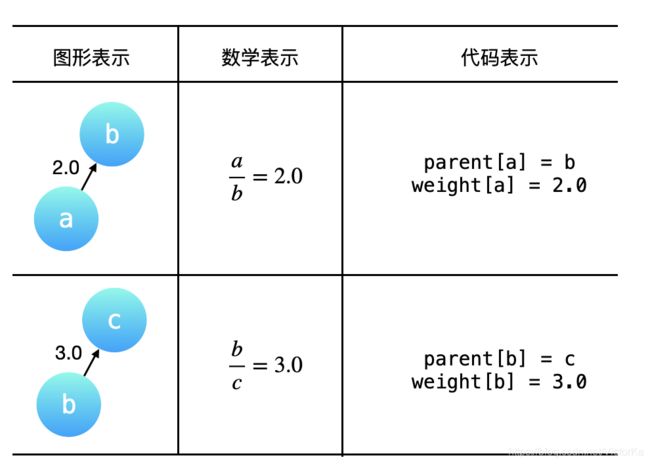
构建有向图:
题目给出的 equations 和 values 可以表示成一个图,equations 中出现的变量就是图的顶点,「分子」于「分母」的比值可以表示成一个有向关系(因为「分子」和「分母」是有序的,不可以对换),并且这个图是一个带权图,values 就是对应的有向边的权值。
「统一变量」与「路径压缩」的关系:
可以把一个一个 query 中的不同变量转换成 同一个变量,这样在计算 query 的时候就可以以 O(1) 的时间复杂度计算出结果,在「并查集」的一个优化技巧中,「路径压缩」就恰好符合了这样的应用场景。
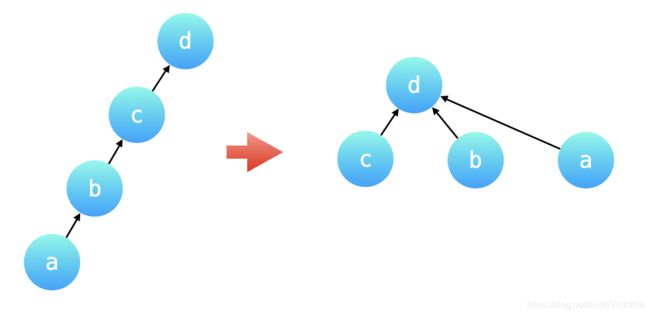
为了避免并查集所表示的树形结构高度过高,影响查询性能。「路径压缩」就是针对树的高度的优化。「路径压缩」的效果是:在查询一个结点 a 的根结点同时,把结点 a 到根结点的沿途所有结点的父亲结点都指向根结点。如下国所示:路径压缩前后,并查集所表示的两棵树形结构等价,路径压缩以后的树的高度为 2,查询性能最好。
由于有「路径压缩」的优化,两个同在一个连通分量中的不同的变量,它们分别到根结点(父亲结点)的权值的比值,就是题目的要求的结果。
在「查询」操作的「路径压缩」优化中维护权值变化:
如下图所示,我们在结点 a 执行一次「查询」操作。路径压缩会先一层一层向上先找到根结点 d,然后依次把 c、b 、a 的父亲结点指向根结点 d。
- c 的父亲结点已经是根结点了,它的权值不用更改;
- b 的父亲结点要修改成根结点,它的权值就是从当前结点到根结点经过的所有有向边的权值的乘积,因此是 3.03.0 乘以 4.04.0 也就是 12.012.0;
- a 的父亲结点要修改成根结点,它的权值就是依然是从当前结点到根结点经过的所有有向边的权值的乘积,但是我们 没有必要把这三条有向边的权值乘起来,这是因为 b 到 c,c 到 d 这两条有向边的权值的乘积,我们在把 b 指向 d 的时候已经计算出来了。因此,a 到根结点的权值就等于 b 到根结点 d 的新的权值乘以 a 到 b 的原来的有向边的权值。
在「合并」操作中维护权值的变化:
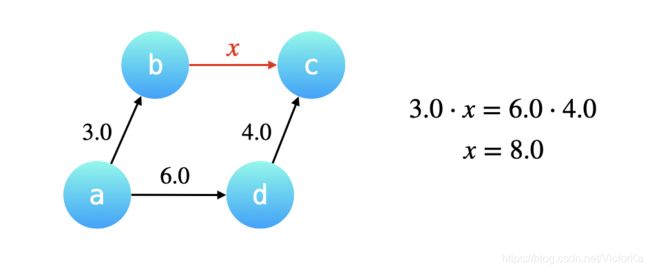
例如已知 a / b = 3.0,d / c = 4.0 ,又已知 a / d = 6.0 ,现在合并结点 a 和 d 所在的集合,其实就是把 a 的根结点 b 指向 d 的根结 c,那么如何计算 b 指向 c 的这条有向边的权重呢?
根据 a 经过 b 可以到达 c,a 经过 d 也可以到达 c,因此 两条路径上的有向边的权值的乘积是一定相等的。设 b 到 c 的权值为 x,那么 3.0 * x = 6.0 *4.0,得 x=8.0。
参考Java代码:
代码思路:先进行预处理,把原本储存在列表中的字符串取出来每个都对应一个id,然后根据id进行并查集操作。事先创建一个并查集数组,数组下标即对应的id。在合并和查询操作的时候要维护权值的变化,find()方法中用递归实现了并查集的路径压缩。最后的isConnected()方法其实就是求解,判断两id是否是同一集合中,若是返回两id指向父节点的权值之商,若不是返回-1。
public class Solution {
public double[] calcEquation(List> equations, double[] values, List> queries) {
int equationsSize = equations.size();
UnionFind unionFind = new UnionFind(2 * equationsSize);
// 第 1 步:预处理,将变量的值与 id 进行映射,使得并查集的底层使用数组实现,方便编码
Map hashMap = new HashMap<>(2 * equationsSize);
int id = 0;
for (int i = 0; i < equationsSize; i++) {
List equation = equations.get(i);
String var1 = equation.get(0);
String var2 = equation.get(1);
if (!hashMap.containsKey(var1)) {
hashMap.put(var1, id);
id++;
}
if (!hashMap.containsKey(var2)) {
hashMap.put(var2, id);
id++;
}
unionFind.union(hashMap.get(var1), hashMap.get(var2), values[i]);
}
// 第 2 步:做查询
int queriesSize = queries.size();
double[] res = new double[queriesSize];
for (int i = 0; i < queriesSize; i++) {
String var1 = queries.get(i).get(0);
String var2 = queries.get(i).get(1);
Integer id1 = hashMap.get(var1);
Integer id2 = hashMap.get(var2);
if (id1 == null || id2 == null) {
res[i] = -1.0d;
} else {
res[i] = unionFind.isConnected(id1, id2);
}
}
return res;
}
private class UnionFind {
private int[] parent;
/**
* 指向的父结点的权值
*/
private double[] weight;
public UnionFind(int n) {
this.parent = new int[n];
this.weight = new double[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
weight[i] = 1.0d;
}
}
public void union(int x, int y, double value) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return;
}
parent[rootX] = rootY;
// 关系式的推导请见「参考代码」下方的示意图
weight[rootX] = weight[y] * value / weight[x];
}
/**
* 路径压缩
*
* @param x
* @return 根结点的 id
*/
public int find(int x) {
if (x != parent[x]) {
int origin = parent[x];
parent[x] = find(parent[x]);
weight[x] *= weight[origin];
}
return parent[x];
}
public double isConnected(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return weight[x] / weight[y];
} else {
return -1.0d;
}
}
}
}
作者:LeetCode
链接:https://leetcode-cn.com/problems/evaluate-division/solution/399-chu-fa-qiu-zhi-nan-du-zhong-deng-286-w45d/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 法二:广度优先搜索
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/evaluate-division/solution/chu-fa-qiu-zhi-by-leetcode-solution-8nxb/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
可以将整个问题建模成一张图:给定图中的一些点(变量),以及某些边的权值(两个变量的比值),试对任意两点(两个变量)求出其路径长(两个变量的比值)。因此,我们首先需要遍历 equations 数组,找出其中所有不同的字符串,并通过哈希表将每个不同的字符串映射成整数。
在构建完图之后,对于任何一个查询,就可以从起点出发,通过广度优先搜索的方式,不断更新起点与当前点之间的路径长度,直到搜索到终点为止。
class Solution {
public double[] calcEquation(List> equations, double[] values, List> queries) {
int nvars = 0;
Map variables = new HashMap();
int n = equations.size();
for (int i = 0; i < n; i++) {
if (!variables.containsKey(equations.get(i).get(0))) {
variables.put(equations.get(i).get(0), nvars++);
}
if (!variables.containsKey(equations.get(i).get(1))) {
variables.put(equations.get(i).get(1), nvars++);
}
}
// 对于每个点,存储其直接连接到的所有点及对应的权值
List[] edges = new List[nvars];
for (int i = 0; i < nvars; i++) {
edges[i] = new ArrayList();
}
for (int i = 0; i < n; i++) {
int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
edges[va].add(new Pair(vb, values[i]));
edges[vb].add(new Pair(va, 1.0 / values[i]));
}
int queriesCount = queries.size();
double[] ret = new double[queriesCount];
for (int i = 0; i < queriesCount; i++) {
List query = queries.get(i);
double result = -1.0;
if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
if (ia == ib) {
result = 1.0;
} else {
Queue points = new LinkedList();
points.offer(ia);
double[] ratios = new double[nvars];
Arrays.fill(ratios, -1.0);
ratios[ia] = 1.0;
while (!points.isEmpty() && ratios[ib] < 0) {
int x = points.poll();
for (Pair pair : edges[x]) {
int y = pair.index;
double val = pair.value;
if (ratios[y] < 0) {
ratios[y] = ratios[x] * val;
points.offer(y);
}
}
}
result = ratios[ib];
}
}
ret[i] = result;
}
return ret;
}
}
class Pair {
int index;
double value;
Pair(int index, double value) {
this.index = index;
this.value = value;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/evaluate-division/solution/chu-fa-qiu-zhi-by-leetcode-solution-8nxb/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 法三:Floyd 算法
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/evaluate-division/solution/chu-fa-qiu-zhi-by-leetcode-solution-8nxb/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
对于查询数量很多的情形,如果为每次查询都独立搜索一次,则效率会变低。为此,我们不妨对图先做一定的预处理,随后就可以在较短的时间内回答每个查询。在本题中,我们可以使用Floyd 算法,预先计算出任意两点之间的距离。
class Solution {
public double[] calcEquation(List> equations, double[] values, List> queries) {
int nvars = 0;
Map variables = new HashMap();
int n = equations.size();
for (int i = 0; i < n; i++) {
if (!variables.containsKey(equations.get(i).get(0))) {
variables.put(equations.get(i).get(0), nvars++);
}
if (!variables.containsKey(equations.get(i).get(1))) {
variables.put(equations.get(i).get(1), nvars++);
}
}
double[][] graph = new double[nvars][nvars];
for (int i = 0; i < nvars; i++) {
Arrays.fill(graph[i], -1.0);
}
for (int i = 0; i < n; i++) {
int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
graph[va][vb] = values[i];
graph[vb][va] = 1.0 / values[i];
}
for (int k = 0; k < nvars; k++) {
for (int i = 0; i < nvars; i++) {
for (int j = 0; j < nvars; j++) {
if (graph[i][k] > 0 && graph[k][j] > 0) {
graph[i][j] = graph[i][k] * graph[k][j];
}
}
}
}
int queriesCount = queries.size();
double[] ret = new double[queriesCount];
for (int i = 0; i < queriesCount; i++) {
List query = queries.get(i);
double result = -1.0;
if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
if (graph[ia][ib] > 0) {
result = graph[ia][ib];
}
}
ret[i] = result;
}
return ret;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/evaluate-division/solution/chu-fa-qiu-zhi-by-leetcode-solution-8nxb/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。