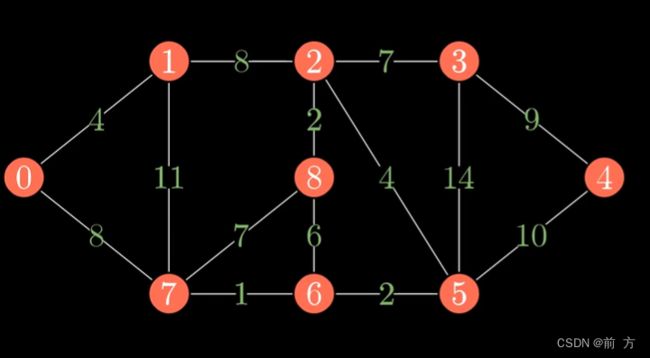
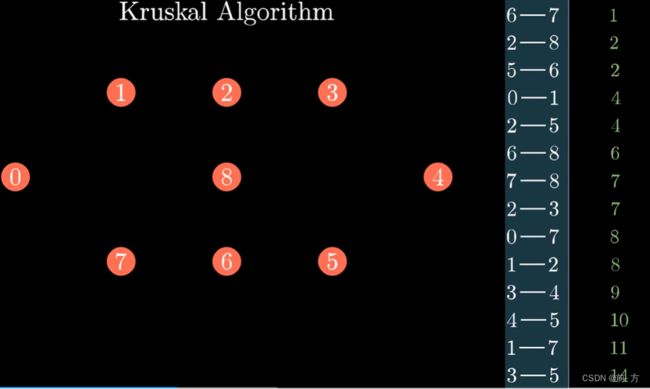
最小生成树(Kruskal)克鲁斯卡尔算法
算法步骤总共分为两步,由并查集实现
第一步(把所有的边按边长的大小进行排序)
第二步(如果两个点不连通就把两点之间的边加上再把两个点连通)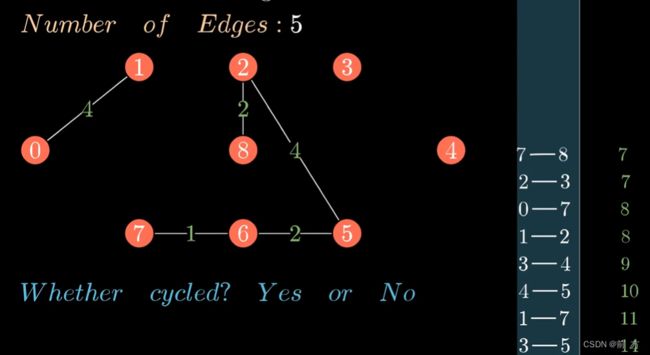
当放入的边数为点数减去一时就代表已经全部连通
例题一(859. Kruskal算法求最小生成树)acwing
给定一个 n 个点 m条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V中的全部 n个顶点和 E 中 n−1条边构成的无向连通子图被称为 G的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤105
1≤m≤2∗105
图中涉及边的边权的绝对值均不超过 1000
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6代码实现
#include
using namespace std;
const int N=100010,INF=0x3f3f3f3f;
int n,m,p[N]; //p[N]存并查集
struct Node{
int a,b,w; //分别存点和边
bool operator<(const Node &x)const{
return w>n>>m;
for(int i=0;i>a>>b>>w;
h[i]={a,b,w};
}
int t=kruskal();
if(t==INF)puts("impossible");
else cout< 例题二(P1546 [USACO3.1] 最短网络 Agri-Net)洛谷
题目背景
Farmer John 被选为他们镇的镇长!他其中一个竞选承诺就是在镇上建立起互联网,并连接到所有的农场。当然,他需要你的帮助。
题目描述
FJ 已经给他的农场安排了一条高速的网络线路,他想把这条线路共享给其他农场。为了用最小的消费,他想铺设最短的光纤去连接所有的农场。
你将得到一份各农场之间连接费用的列表,你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过 10^5。
输入格式
第一行农场的个数 N(3≤N≤100)。
接下来是一个N×N 的矩阵,表示每个农场之间的距离。理论上,他们是 N 行,每行由 N 个用空格分隔的数组成,实际上,由于每行 80 个字符的限制,因此,某些行会紧接着另一些行。当然,对角线将会是 0,因为不会有线路从第 i 个农场到它本身。
输出格式
只有一个输出,其中包含连接到每个农场的光纤的最小长度。
输入输出样例
输入
4 0 4 9 21 4 0 8 17 9 8 0 16 21 17 16 0
输出
28
说明/提示
题目翻译来自NOCOW。
USACO Training Section 3.1
代码实现
#include
using namespace std;
const int N=1e4+10,INF=0x3f3f3f3f;
struct Node{
int a,b,w;
bool operator <(const Node &x)const{ //重载,按从小到大排序
return w>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
int k;
cin>>k;
if(j>i){ //只需要存入一半的边数
h[++c]={i,j,k};
}
}
}
cout<