【计算机视觉|生成对抗】改进的生成对抗网络（GANs）训练技术

本系列博文为深度学习/计算机视觉论文笔记，转载请注明出处

标题：Improved Techniques for Training GANs

链接：[1606.03498v1] Improved Techniques for Training GANs (arxiv.org)

摘要

本文介绍了一系列应用于生成对抗网络（GANs）框架的新的架构特性和训练过程。我们专注于GAN的两个应用领域：半监督学习以及生成人类视觉上逼真的图像。与大多数有关生成模型的研究不同，我们的主要目标不是训练一个将测试数据分配高概率的模型，我们也不要求模型在不使用任何标签的情况下能够学习得很好。通过我们的新技术，我们在MNIST、CIFAR-10和SVHN的半监督分类任务中取得了最先进的结果。生成的图像具有很高的质量，经过视觉图灵测试确认：我们的模型生成的MNIST样本与真实数据无法区分，而CIFAR-10样本的人类错误率为21.3%。我们还展示了具有前所未有分辨率的ImageNet样本，并且表明我们的方法使模型能够学习识别ImageNet类别的特征。

1 引言

生成对抗网络（Generative Adversarial Networks，简称GANs）是一类基于博弈论的学习生成模型的方法[1]。GANs的目标是训练一个生成器网络 $G(z;{\theta }^{(G)})$，通过将噪声向量 $z$ 转换为样本 $x=G(z;{\theta }^{(G)})$，从数据分布 $p_{data}(x)$ 中生成样本。生成器 $G$ 的训练信号来自一个判别器网络 $D(x)$，该网络被训练用于区分生成器分布 $p_{model}(x)$ 的样本和真实数据。生成器网络 $G$ 反过来被训练，以使判别器接受其输出为真实样本。

最近GANs的应用表明它们可以生成优质的样本[2, 3]。然而，训练GANs需要找到一个具有连续、高维参数的非凸博弈的纳什均衡点。通常使用梯度下降技术来训练GANs，这些技术旨在找到代价函数的较低值，而不是找到博弈的纳什均衡。当用于寻找纳什均衡时，这些算法可能无法收敛[4]。

在本文中，我们引入了几种技术，旨在鼓励GANs博弈的收敛。这些技术是基于对非收敛问题的启发式理解而提出的，它们导致了改进的半监督学习性能和改进的样本生成。我们希望其中一些技术可以成为未来工作的基础，提供收敛性的形式保证。

所有代码和超参数可在以下链接找到：https://github.com/openai/improved_gan

2 相关工作

近期有几篇论文专注于改进GAN样本的训练稳定性和生成品质[2, 3, 5, 6]。我们在本文中借鉴了其中一些技术。例如，我们在本文中使用了Radford等人提出的“DCGAN”架构创新，如下所述。

我们提出的其中一种技术，特征匹配，在第3.1节中讨论，与使用最大均值差异[7, 8, 9]训练生成器网络[10, 11]的方法在精神上类似。我们提出的另一种技术，小批量特征，部分基于用于批归一化[12]的思想，而我们提出的虚拟批归一化则是批归一化的直接扩展。

本工作的主要目标之一是提高生成对抗网络在半监督学习中的效果（通过在额外的无标签示例上学习，改善有监督任务，本例中是分类任务的性能）。与许多深度生成模型一样，GANs以前已被应用于半监督学习[13, 14]，我们的工作可以看作是这一努力的延续和改进。

3 迈向收敛的GAN训练

训练生成对抗网络（GANs）涉及寻找一个两个玩家的非合作博弈的纳什均衡点。每个玩家希望最小化其自己的代价函数，对于判别器来说是 $J^{(D)}({\theta }^{(D)},{\theta }^{(G)})$，对于生成器来说是 $J^{(G)}({\theta }^{(D)},{\theta }^{(G)})$。纳什均衡是一个点 $({\theta }^{(D)},{\theta }^{(G)})$，使得 $J^{(D)}$ 在 ${\theta }^{(D)}$ 方面达到最小值，而 $J^{(G)}$ 在 ${\theta }^{(G)}$ 方面达到最小值。然而，寻找纳什均衡是一个非常困难的问题。虽然对于特定情况存在一些算法，但我们不知道有任何适用于GAN博弈的方法，其中代价函数是非凸的，参数是连续的，且参数空间极高维。

每个玩家的最小化代价函数即纳什均衡的观念似乎直观地支持使用传统的基于梯度的最小化技术同时最小化每个玩家的代价。然而，减小 ${\theta }^{(D)}$ 以减少 $J^{(D)}$ 可能会增加 $J^{(G)}$，而减小 ${\theta }^{(G)}$ 以减少 $J^{(G)}$ 可能会增加 $J^{(D)}$。梯度下降因此在许多博弈中无法收敛。例如，当一个玩家相对于 $x$ 最小化 $xy$，而另一个玩家相对于 $y$ 最小化 $-xy$，梯度下降进入一个稳定轨道，而不是收敛到期望的均衡点 $x=y=0$ [15]。因此，以前的GAN训练方法在每个玩家的代价上同时应用梯度下降，尽管没有保证此过程将收敛。我们引入了以下启发式的技术，以鼓励收敛：

3.1 特征匹配（Feature matching）

特征匹配通过为生成器指定一个新的目标来解决GAN的不稳定性问题，该目标防止生成器在当前判别器上过度训练。新的目标要求生成器不是直接最大化判别器的输出，而是要求生成器生成与真实数据统计相匹配的数据，我们只使用判别器来指定值得匹配的统计数据。具体来说，我们训练生成器以匹配判别器中间层的特征的期望值。这是生成器选择要匹配的统计数据的自然选择，因为通过训练判别器，我们要求它找到最能区分实际数据和当前模型生成数据的特征。

设 $f(x)$ 表示判别器中间层的激活，我们为生成器定义的新目标是：$||{\mathbb{E}}_{x\sim p_{data}}f(x)-{\mathbb{E}}_{z\sim p_z(z)}f(G(z))|{|}_2^2$。判别器和 $f(x)$ 均以通常的方式训练。与常规的GAN训练一样，该目标具有一个固定点，其中 $G$ 完全匹配训练数据的分布。我们不能保证在实践中达到这一固定点，但我们的实证结果表明，特征匹配在常规GAN变得不稳定的情况下确实是有效的。

3.2 小批量判别（Minibatch discrimination）

GAN的主要失败模式之一是生成器崩溃到一个参数设置，使其始终发出相同的点。当即将崩溃为单一模式时，许多相似点的判别器梯度可能指向相似的方向。因为判别器独立地处理每个示例，所以其梯度之间没有协调，因此没有机制告诉生成器的输出变得更不相似。相反，所有的输出都趋向于一个判别器当前认为非常逼真的单一点。崩溃发生后，判别器学习到这个单一点来自生成器，但梯度下降无法分开相同的输出。判别器的梯度随后将生成器产生的单一点永远推到空间中，算法无法收敛到具有正确熵量的分布。避免这种类型失败的一个明显策略是允许判别器查看多个数据示例的组合，并进行我们称之为小批量判别。

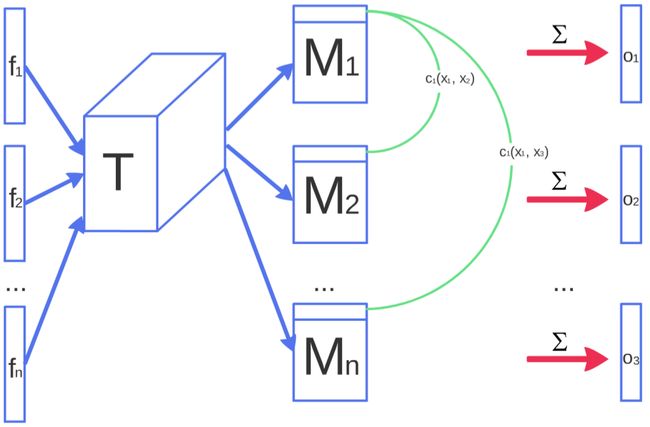
小批量判别的概念非常普遍：任何判别器模型，它查看多个示例的组合，而不是孤立地查看，都有可能有助于避免生成器的崩溃。实际上，Radford等人通过在判别器中成功应用批归一化的做法[3]从这个角度解释得很好。然而，到目前为止，我们的实验仅限于明确旨在识别特别接近的生成器样本的模型。一个成功的规范是对建模小批量中示例之间的紧密程度的如下描述：令 $f(x_i)\in {\mathbb{R}}^A$ 表示输入 $x_i$ 在判别器的某个中间层产生的特征向量。然后，将向量 $f(x_i)$ 与张量 $T\in {\mathbb{R}}^{A\times B\times C}$ 相乘，得到矩阵 $M_i\in {\mathbb{R}}^{B\times C}$。然后，计算结果矩阵 $M_i$ 的行之间的L1距离，跨越样本 $i\in \{1,2,...,n\}$，并应用负指数函数（图1）：$c_b(x_i,x_j)=exp(-||M_{i,b}-M_{j,b}|{|}_{L1})\in \mathbb{R}$。小批量层的输出 $o(x_i)$ 对于样本 $x_i$ 定义为与所有其他样本的 $c_b(x_i,x_j)$ 之和：

$$\begin{array}{rl}o(x_i{)}_b& =\sum _{j=1}^n{c}_b(x_i,x_j)\in \mathbb{R}\\ o(x_i)& =[o(x_i{)}_1,o(x_i{)}_2,...,o(x_i{)}_B]\in {\mathbb{R}}^B\\ o(X)& \in {\mathbb{R}}^{n\times B}\end{array}$$

图1：图示了小批量判别的工作原理。来自样本 $x_i$ 的特征 $f(x_i)$ 通过张量 $T$ 相乘，并计算交叉样本距离。

接下来，我们将小批量层的输出 $o(x_i)$ 与作为其输入的中间特征 $f(x_i)$ 进行连接，然后将结果输入判别器的下一层。我们分别为来自生成器和训练数据的样本计算这些小批量特征。与以前一样，判别器仍需要为每个示例输出一个单一数字，指示其来自训练数据的可能性：判别器的任务实际上仍然是将单个示例分类为真实数据还是生成数据，但现在它能够使用小批量中的其他示例作为辅助信息。小批量判别使我们能够快速生成视觉吸引人的样本，在这方面它优于特征匹配（第6节）。有趣的是，然而，特征匹配在使用第5节中描述的半监督学习方法来获得强分类器方面表现更好。

3.3 历史平均法（Historical averaging）

在应用这种技术时，我们修改每个玩家的代价，包括一个项 $||\theta -\frac{1}{t}{\sum }_{i=1}^t\theta [i]|{|}^2$，其中 $\theta [i]$ 是过去时间点 i 处的参数值。参数的历史平均可以以在线方式更新，因此这种学习规则适用于长时间序列。这种方法受到虚拟游戏[16]算法的启发，该算法可以在其他类型的游戏中找到均衡点。我们发现，我们的方法能够找到低维连续非凸博弈的均衡点，例如，一个玩家控制 $x$，另一个玩家控制 $y$，价值函数为 $(f(x)-1)(y-1)$，其中 $f(x)=x$（对于 $x<0$）和 $f(x)=x^2$（其他情况）。对于这些玩具游戏，梯度下降失败，进入不逼近均衡点的扩展轨道。

3.4 单侧标签平滑（One-sided label smoothing）

标签平滑是20世纪80年代的一项技术，最近由Szegedy等人[17]独立重新发现，它用平滑的值（如0.9或0.1）替换分类器的0和1目标，并且最近被证明可以减少神经网络对对抗性示例的脆弱性[18]。将正分类目标替换为α，负目标替换为β，最优判别器变为 $D(x)=\frac{\alpha p_{data}(x)+\beta p_{model}(x)}{p_{data}(x)+p_{model}(x)}$。分子中的 $p_{model}$ 的存在是有问题的，因为在 $p_{data}$ 接近零且 $p_{model}$ 较大的区域中，来自 $p_{model}$ 的错误样本没有动力靠近数据。因此，我们只对正标签进行平滑处理，将负标签设为0。

3.5 虚拟批归一化（Virtual batch normalization）

批归一化极大地改善了神经网络的优化，并且已被证明对DCGANs[3]非常有效。然而，它导致神经网络对于输入示例 $x$ 的输出在同一小批量中的其他输入 $x_0$ 高度相关。为了避免这个问题，我们引入虚拟批归一化（VBN），其中每个示例 $x$ 基于对参考示例批次的统计信息进行归一化，这些参考示例在训练开始时被选择一次并固定下来，以及基于 $x$ 本身。参考批次仅使用其自己的统计数据进行归一化。VBN在计算上是昂贵的，因为它需要在两个数据小批次上运行前向传播，因此我们仅在生成器网络中使用它。

4 图像质量评估

生成对抗网络缺乏客观函数，这使得比较不同模型的性能变得困难。一种直观的性能指标可以通过让人类标注员评估样本的视觉质量来获得[2]。我们使用Amazon Mechanical Turk（MTurk）自动化这个过程，使用图中的网络界面（位于 http://infinite-chamber-35121.herokuapp.com/cifar-minibatch/），我们用它来要求标注员区分生成数据和真实数据。我们模型的质量评估结果在第6节中进行了描述。

使用人类标注员的一个不足之处是指标会根据任务的设置和标注员的动机而变化。我们还发现，当我们为标注员提供有关他们错误的反馈时，结果会发生很大变化：通过从这些反馈中学习，标注员能够更好地指出生成图像中的缺陷，从而给出更为悲观的质量评估。图2的左列呈现了标注过程中的一个屏幕，而右列显示了我们如何通知标注员其错误。

图2：提供给标注员的网络界面。要求标注员区分计算机生成的图像和真实图像。

作为人类标注员的替代方案，我们提出了一种自动方法来评估样本，我们发现这种方法与人类评估很好地相关：我们将Inception模型¹ [19] 应用于每个生成的图像，以获得条件标签分布 $p(y|x)$。包含有意义对象的图像应该具有低熵的条件标签分布 $p(y|x)$。此外，我们期望模型生成各种各样的图像，因此边缘分布 $p(y|x=G(z))dz$ 应该具有高熵。结合这两个要求，我们提出的度量是：$exp(E_{x}KL(p(y|x)||p(y)))$，我们对结果进行指数化，以便更容易比较值。我们的Inception得分与CatGAN [14]中用于训练生成模型的目标密切相关：虽然我们在训练时没有取得太大成功，但我们发现它是一个很好的评估指标，与人类判断非常相关。我们发现，在评估这个指标时，对足够多的样本（即50k）进行评估是很重要的，因为该指标的一部分衡量了多样性。

5 半监督学习

考虑一个用于将数据点 $x$ 分类为 $K$ 个可能类别之一的标准分类器。这样的模型将 $x$ 作为输入，并输出一个 K 维的对数向量 {$l_1,...,l_K$}，可以通过应用 softmax 转化为类别概率：$p_{\text{model}}(y=j|x)=\frac{exp(l_j)}{{\sum }_{k=1}^{K}exp(l_k)}$。在监督学习中，这样的模型通过最小化观察到的标签与模型预测分布 $p_{\text{model}}(y|x)$ 之间的交叉熵来进行训练。

我们可以通过将来自 GAN 生成器 $G$ 的样本添加到我们的数据集中来使用任何标准分类器进行半监督学习，将它们标记为新的 “生成” 类别 $y=K+1$，并相应地将我们的分类器输出维度从 $K$ 增加到 $K+1$。然后我们可以使用 $p_{\text{model}}(y=K+1|x)$ 来提供 $x$ 是假的概率，对应于原始 GAN 框架中的 $1-D(x)$。现在，我们还可以从无标签数据中进行学习，只要我们知道它与 $K$ 类真实数据之一相对应，通过最大化 $log{p}_{\text{model}}(y\in \{1,...,K\}|x)$。

假设我们的数据集一半是真实数据，一半是生成的数据（这是任意的），我们用于训练分类器的损失函数则变为：

$$\begin{array}{rl}L& =-{\mathbb{E}}_{x,y\sim p_{\text{data}}(x,y)}[\log p_{\text{model}}(y|x)]-{\mathbb{E}}_{x\sim G}[\log p_{\text{model}}(y=K+1|x)]\\ & =L_{\text{supervised}}+L_{\text{unsupervised}}\end{array}$$

，其中

$$\begin{array}{rl}{L}_{\text{supervised}}& =-{\mathbb{E}}_{x,y\sim p_{\text{data}}(x,y)}\log p_{\text{model}}(y|x,y<K+1)\\ L_{\text{unsupervised}}& =-\{{\mathbb{E}}_{x\sim p_{\text{data}}(x)}\log [1-p_{\text{model}}(y=K+1|x)]+{\mathbb{E}}_{x\sim G}\log [p_{\text{model}}(y=K+1|x)]\}\end{array}$$
在这里，我们将总的交叉熵损失分解为标准监督损失函数 $L_{\text{supervised}}$（给定数据为真时标签的负对数概率）和一个无监督损失 $L_{\text{unsupervised}}$，事实上，它就是标准的 GAN 博弈值，当我们将 $D(x)=1-p_{\text{model}}(y=K+1|x)$ 代入表达式时，这一点变得明显：
$L_{\text{unsupervised}}=-\{{\mathbb{E}}_{x\sim p_{\text{data}}(x)}\log D(x)+{\mathbb{E}}_{z\sim \text{noise}}\log (1-D(G(z)))\}$。

最小化 $L_{\text{supervised}}$ 和 $L_{\text{unsupervised}}$ 的最佳解是使 $exp[l_j(x)]=c(x)p(y=j,x)$ 对所有 $j<K+1$，以及 $exp[l_{K+1}(x)]=c(x)p_G(x)$，其中 $c(x)$ 是一个未确定的缩放函数。因此，无监督损失从 Sutskever 等人 [13] 的角度来看与监督损失是一致的，我们可以通过共同最小化这两个损失函数来更好地从数据中估计这个最优解。实际上，当对于我们的分类器来说，最小化 $L_{\text{unsupervised}}$ 不是微不足道的时，$L_{\text{unsupervised}}$ 可能会有所帮助，因此我们需要训练 $G$ 来近似数据分布。一种做法是通过训练 $G$ 来最小化 GAN 博弈值，使用由我们的分类器定义的判别器 $D$。这种方法引入了 $G$ 和我们的分类器之间的相互作用，我们尚未完全理解，但实际上我们发现，使用特征匹配 GAN 来优化 $G$ 在半监督学习中非常有效，而使用带有小批次判别的 GAN 来训练 $G$ 则根本不起作用。在这里，我们使用这种方法呈现我们的实证结果；使用这种方法开发关于 $D$ 和 $G$ 之间相互作用的完整理论理解将留待将来的工作。

最后，注意我们的具有 K + 1 输出的分类器是过度参数化的：从每个输出逻辑中减去一个一般函数 f(x)，即将 $l_j(x)\leftarrow l_j(x)-f(x)$ 对所有 $j$，不会改变 softmax 的输出。这意味着我们可以等效地固定 $l_{K+1}(x)=0$ 对所有 $x$，在这种情况下，$L_{\text{supervised}}$ 变为我们原始具有 K 个类别的分类器的标准监督损失函数，而我们的判别器 $D$ 给出为 $D(x)=\frac{Z(x)}{Z(x)+1}$，其中 $Z(x)={\sum }_{k=1}^{K}exp[l_k(x)]$。

5.1 标签对图像质量的重要性

除了在半监督学习方面取得了最先进的结果，上述方法还具有出乎意料的效果，即通过人类标注员的评价来改善生成图像的质量。原因似乎是人类视觉系统对能够帮助推断图像所代表的对象类别的图像统计信息非常敏感，而对于解释图像的不太重要的局部统计信息可能相对不太敏感。这得到了我们在第4节中开发的Inception得分和人类标注员报告的质量之间高度相关性的支持，该得分明确构建用于衡量生成图像的“物体性”。通过让判别器 $D$ 对图像中显示的对象进行分类，我们会使其形成一个内部表示，强调与人类强调的相同特征。这种效果可以理解为一种迁移学习的方法，可能可以更广泛地应用。我们将进一步探讨这种可能性留待未来的工作。

6 实验

我们在 MNIST、CIFAR-10 和 SVHN 数据集上进行了半监督实验，并在 MNIST、CIFAR-10、SVHN 和 ImageNet 数据集上进行了样本生成实验。我们提供了复现大部分实验的代码。

6.1 MNIST

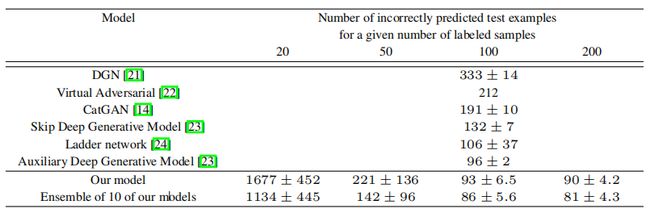
MNIST 数据集包含 60,000 个标记的手写数字图像。我们进行半监督训练，随机选择其中的一小部分，考虑使用 20、50、100 和 200 个带标签的示例进行设置。结果在 10 个随机子集上进行平均，每个子集都被选择为每个类别都有平衡数量的示例。其余的训练图像则没有标签。我们的网络各有 5 个隐藏层。我们使用权重归一化 [20]，并在判别器的每一层的输出上添加高斯噪声。表格 1 总结了我们的结果。

表1：在具有置换不变性的 MNIST 上的半监督设置中被错误分类的测试示例数量。结果在 10 个种子上进行平均。

使用特征匹配（第3.1节）在半监督学习期间生成的生成器样本在视觉上看起来不太吸引人（左图3）。相反，使用小批次判别（第3.2节），我们可以改善它们的视觉质量。在 MTurk 上，标注员在52.4％的情况下（共2000个投票）能够区分样本，其中随机猜测会获得50％的准确率。同样地，我们机构的研究人员也没有找到任何可以用来区分样本的痕迹。然而，使用小批次判别的半监督学习并没有产生与特征匹配一样好的分类器。

图3：（左）在半监督训练期间由模型生成的样本。这些样本可以明显地与来自 MNIST 数据集的图像区分开来。（右）使用小批次判别生成的样本。这些样本与数据集中的图像完全无法区分。

6.2 CIFAR-10

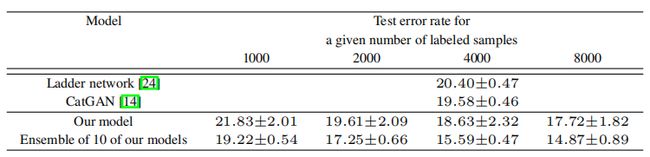
CIFAR-10 是一个小型且经过广泛研究的 32 × 32 的自然图像数据集。我们使用这个数据集来研究半监督学习，以及检查可以实现的样本的视觉质量。对于我们的 GAN 中的判别器，我们使用了一个有 9 层深度的卷积神经网络，并加入了 dropout 和权重归一化。生成器是一个有 4 层深度的卷积神经网络，并使用了批归一化。表 2 总结了我们在半监督学习任务上的结果。

表2：在半监督 CIFAR-10 上的测试错误。结果在数据的 10 个拆分上进行平均。

当我们使用我们最好的 CIFAR-10 模型生成了50％的真实数据和50％的虚假数据时，MTurk 用户正确分类了78.7％的图像。然而，MTurk 用户可能对 CIFAR-10 图像不太熟悉或者动机不足；我们自己则能以 >95％ 的准确率对图像进行分类。我们通过观察到，在根据 Inception 得分仅使用前1％的样本进行过滤时，MTurk 的准确率降至71.4％，从而验证了上述描述的 Inception 得分。我们进行了一系列的消融实验，以证明我们提出的技术提高了 Inception 得分，结果总结在表3 中。我们还展示了这些消融实验的图像 — 在我们看来，Inception 得分与我们对图像质量的主观判断相关良好。数据集的样本达到了最高值。所有甚至部分崩溃的模型得分都相对较低。我们警告说，Inception 得分应该被用作粗略指导来评估通过某些独立标准进行训练的模型；直接优化 Inception 得分会导致产生对抗性示例 [25]。

图4：在半监督 CIFAR-10 上使用特征匹配（第3.1节，左）和小批次判别（第3.2节，右）训练期间生成的样本。

6.3 SVHN

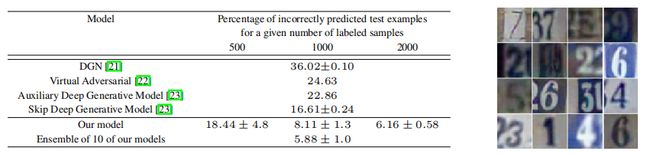
对于 SVHN 数据集，我们使用了与 CIFAR-10 相同的体系结构和实验设置。

图5：（左）在 SVHN 上的错误率。（右）来自 SVHN 生成器的样本。

表 3：不同模型生成的样本的 Inception 得分表，用于 50,000 张图像。得分与人类判断高度相关，自然图像的得分最高。生成坍缩样本的模型得分相对较低。这个指标使我们不必依赖人类评估。“我们的方法”包括本文中描述的所有技术，但不包括特征匹配和历史平均。其余的实验是消融实验，显示我们的技术是有效的。“-VBN+BN” 在生成器中将 VBN 替换为 BN，与 DCGANs 一样。这会在 CIFAR 上导致样本质量小幅下降。VBN 对 ImageNet 更为重要。“-L+HA” 从训练过程中删除标签，并添加历史平均来进行补偿。HA 使得仍然能够生成一些可识别的对象。没有 HA，样本质量会大幅降低（见“-L”）。 “-LS” 移除标签平滑，并导致相对于“我们的方法”明显的性能下降。“-MBF” 移除小批次特征，并导致非常大的性能下降，甚至比移除标签引起的下降还要大。添加 HA 不能防止这个问题。

6.4 ImageNet

我们在一个规模前所未有的数据集上测试了我们的技术：来自ILSVRC2012数据集的128×128图像，拥有1,000个类别。据我们所知，以前没有任何出版物将生成模型应用于具有这么高分辨率和这么多对象类别的数据集。由于生成模型倾向于低估分布中的熵，大量的对象类别对GANs特别具有挑战性。我们广泛修改了一个公开可用的TensorFlow [26]实现的DCGANs²，使用了多GPU实现来实现高性能。未经修改的DCGANs可以学习一些基本的图像统计信息，并生成具有某种自然颜色和纹理的连续形状，但不会学习任何对象。使用本文中描述的技术，GANs学会生成类似动物的对象，但解剖学不正确。结果如图6所示。

图6：从ImageNet数据集生成的样本。 （左）由DCGAN生成的样本。 （右）使用本文提出的技术生成的样本。新技术使得GAN能够学习到动物的可识别特征，如毛皮、眼睛和鼻子，但这些特征未能正确地结合形成具有现实解剖结构的动物。

7 结论

生成对抗网络是一类有前途的生成模型，但迄今为止，其不稳定的训练和缺乏适当的评估指标一直是限制因素。本研究提出了这两个问题的部分解决方案。我们提出了几种稳定训练的技术，使我们能够训练以前无法训练的模型。此外，我们提出的评估指标（Inception分数）为我们比较这些模型的质量提供了基础。我们将我们的技术应用于半监督学习问题，在计算机视觉中的多个不同数据集上实现了最先进的结果。本研究的贡献具有实际意义；我们希望在未来的研究中能够发展出更严谨的理论理解。

参考文献

1. Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza等。生成对抗网络。在NIPS，2014年。
2. Emily Denton，Soumith Chintala，Arthur Szlam和Rob Fergus。使用Laplacian金字塔的深度生成图像模型。arXiv预印本arXiv：1506.05751，2015年。
3. Alec Radford，Luke Metz和Soumith Chintala。深度卷积生成对抗网络中的无监督表示学习。arXiv预印本arXiv：1511.06434，2015年。
4. Ian J Goodfellow。关于估计生成模型的可分辨性标准。arXiv预印本arXiv：1412.6515，2014年。
5. Daniel Jiwoong Im，Chris Dongjoo Kim，Hui Jiang和Roland Memisevic。使用循环对抗网络生成图像。arXiv预印本arXiv：1602.05110，2016年。
6. Donggeun Yoo，Namil Kim，Sunggyun Park，Anthony S Paek和In So Kweon。像素级域转换。arXiv预印本arXiv：1603.07442，2016年。
7. Arthur Gretton，Olivier Bousquet，Alex Smola和Bernhard Sch¨olkopf。使用Hilbert-Schmidt范数测量统计依赖性。在算法学习理论，第63-77页。Springer，2005年。
8. Kenji Fukumizu，Arthur Gretton，Xiaohai Sun和Bernhard Sch¨olkopf。条件依赖的核测度。在NIPS，第20卷，第489-496页，2007年。
9. Alex Smola，Arthur Gretton，Le Song和Bernhard Sch¨olkopf。分布的Hilbert空间嵌入。在算法学习理论，第13-31页。Springer，2007年。
10. Yujia Li，Kevin Swersky和Richard S. Zemel。生成矩匹配网络。CoRR，abs/1502.02761，2015年。
11. Gintare Karolina Dziugaite，Daniel M Roy和Zoubin Ghahramani。通过最大均值差异优化训练生成神经网络。arXiv预印本arXiv：1505.03906，2015年。
12. Sergey Ioffe和Christian Szegedy。通过减少内部协变量偏移来加速深度网络训练的批量归一化。arXiv预印本arXiv：1502.03167，2015年。
13. Ilya Sutskever，Rafal Jozefowicz，Karol Gregor等。走向基于原则的无监督学习。arXiv预印本arXiv：1511.06440，2015年。
14. Jost Tobias Springenberg。使用分类生成对抗网络的无监督和半监督学习。arXiv预印本arXiv：1511.06390，2015年。
15. Ian Goodfellow，Yoshua Bengio和Aaron Courville。深度学习。2016年。MIT出版社。
16. George W Brown。通过虚拟游戏的迭代解决游戏。生产和分配的活动分析，第13卷，第374-376页，1951年。
17. C. Szegedy，V. Vanhoucke，S. Ioffe，J. Shlens和Z. Wojna。重新思考计算机视觉的Inception架构。ArXiv e-prints，2015年12月。
18. David Warde-Farley和Ian Goodfellow。深度神经网络的敌对扰动。在Tamir Hazan，George Papandreou和Daniel Tarlow的编辑下，扰动、优化和统计，第11章。2016年。MIT出版社正在筹备中的书。
19. Christian Szegedy，Vincent Vanhoucke，Sergey Ioffe，Jonathon Shlens和Zbigniew Wojna。重新思考计算机视觉的创始架构。arXiv预印本arXiv：1512.00567，2015年。
20. Tim Salimans和Diederik P Kingma。权重归一化：一种简单的重新参数化加速深度神经网络的方法。arXiv预印本arXiv：1602.07868，2016年。
21. Diederik P Kingma，Shakir Mohamed，Danilo Jimenez Rezende和Max Welling。具有深度生成模型的半监督学习。在神经信息处理系统中，2014年。
22. Takeru Miyato，Shin-ichi Maeda，Masanori Koyama，Ken Nakae和Shin Ishii。通过虚拟对抗性示例进行分布平滑。arXiv预印本arXiv：1507.00677，2015年。
23. Lars Maaløe，Casper Kaae Sønderby，Søren Kaae Sønderby和Ole Winther。辅助深度生成模型。arXiv预印本arXiv：1602.05473，2016年。
24. Antti Rasmus，Mathias Berglund，Mikko Honkala，Harri Valpola和Tapani Raiko。具有梯田网络的半监督学习。在神经信息处理系统的进展中，2015年。
25. Christian Szegedy，Wojciech Zaremba，Ilya Sutskever等。神经网络的有趣属性。arXiv预印本arXiv：1312.6199，2013年。
26. Mart´ın Abadi，Ashish Agarwal，Paul Barham等。TensorFlow：在异构系统上进行大规模机器学习，2015年。软件可在tensorflow.org上获得。

References

1. Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, et al. Generative adversarial nets. In NIPS, 2014.
2. Emily Denton, Soumith Chintala, Arthur Szlam, and Rob Fergus. Deep generative image models using a Laplacian pyramid of adversarial networks. arXiv preprint arXiv:1506.05751, 2015.
3. Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434, 2015.
4. Ian J Goodfellow. On distinguishability criteria for estimating generative models. arXiv preprint arXiv:1412.6515, 2014.
5. Daniel Jiwoong Im, Chris Dongjoo Kim, Hui Jiang, and Roland Memisevic. Generating images with recurrent adversarial networks. arXiv preprint arXiv:1602.05110, 2016.
6. Donggeun Yoo, Namil Kim, Sunggyun Park, Anthony S Paek, and In So Kweon. Pixel-level domain transfer. arXiv preprint arXiv:1603.07442, 2016.
7. Arthur Gretton, Olivier Bousquet, Alex Smola, and Bernhard Sch¨olkopf. Measuring statistical dependence with Hilbert-Schmidt norms. In Algorithmic learning theory, pages 63–77. Springer, 2005.
8. Kenji Fukumizu, Arthur Gretton, Xiaohai Sun, and Bernhard Sch¨olkopf. Kernel measures of conditional dependence. In NIPS, volume 20, pages 489–496, 2007.
9. Alex Smola, Arthur Gretton, Le Song, and Bernhard Sch¨olkopf. A Hilbert space embedding for distributions. In Algorithmic learning theory, pages 13–31. Springer, 2007.
10. Yujia Li, Kevin Swersky, and Richard S. Zemel. Generative moment matching networks. CoRR, abs/1502.02761, 2015.
11. Gintare Karolina Dziugaite, Daniel M Roy, and Zoubin Ghahramani. Training generative neural networks via maximum mean discrepancy optimization. arXiv preprint arXiv:1505.03906, 2015.
12. Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167, 2015.
13. Ilya Sutskever, Rafal Jozefowicz, Karol Gregor, et al. Towards principled unsupervised learning. arXiv preprint arXiv:1511.06440, 2015.
14. Jost Tobias Springenberg. Unsupervised and semi-supervised learning with categorical generative adversarial networks. arXiv preprint arXiv:1511.06390, 2015.
15. Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning. 2016. MIT Press.
16. George W Brown. Iterative solution of games by fictitious play. Activity analysis of production and allocation, 13(1):374–376, 1951.
17. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna. Rethinking the Inception Architecture for Computer Vision. ArXiv e-prints, December 2015.
18. David Warde-Farley and Ian Goodfellow. Adversarial perturbations of deep neural networks. In Tamir Hazan, George Papandreou, and Daniel Tarlow, editors, Perturbations, Optimization, and Statistics, chapter 11. 2016. Book in preparation for MIT Press.
19. Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna. Rethinking the inception architecture for computer vision. arXiv preprint arXiv:1512.00567, 2015.
20. Tim Salimans and Diederik P Kingma. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. arXiv preprint arXiv:1602.07868, 2016.
21. Diederik P Kingma, Shakir Mohamed, Danilo Jimenez Rezende, and Max Welling. Semi-supervised learning with deep generative models. In Neural Information Processing Systems, 2014.
22. Takeru Miyato, Shin-ichi Maeda, Masanori Koyama, Ken Nakae, and Shin Ishii. Distributional smoothing by virtual adversarial examples. arXiv preprint arXiv:1507.00677, 2015.
23. Lars Maaløe, Casper Kaae Sønderby, Søren Kaae Sønderby, and Ole Winther. Auxiliary deep generative models. arXiv preprint arXiv:1602.05473, 2016.
24. Antti Rasmus, Mathias Berglund, Mikko Honkala, Harri Valpola, and Tapani Raiko. Semi-supervised learning with ladder networks. In Advances in Neural Information Processing Systems, 2015.
25. Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, et al. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199, 2013.
26. Mart´ın Abadi, Ashish Agarwal, Paul Barham, et al. TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. Software available from tensorflow.org.
    perties of neural networks. arXiv preprint arXiv:1312.6199, 2013.
27. Mart´ın Abadi, Ashish Agarwal, Paul Barham, et al. TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. Software available from tensorflow.org.

---

1. 我们使用预训练的Inception模型，下载链接为 http://download.tensorflow.org/models/image/imagenet/inception-2015-12-05.tgz。在发表时，将提供使用该模型计算Inception得分的代码。 ↩︎

2. https://github.com/carpedm20/DCGAN-tensorflow ↩︎