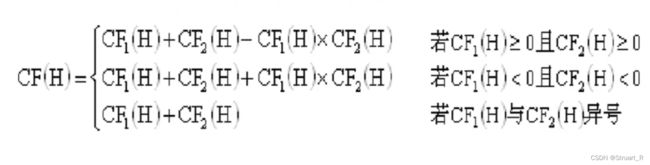人工智能原理(5)
目录
一、不确定性推理
1、不确定性推理含义
2、知识不确定性的来源
3、不确定推理要解决的基本问题
4、不确定性推理方法分类
二、主观贝叶斯方法
1、主观贝叶斯方法
2、知识不确定性的表示
3、证据
4、不确定性的更新
三、可信度方法
1、可信度模型
2、性质
3、可信度方法特点
四、证据理论
1、概率分配函数
2、信任函数
3、似然函数
4、性质
5、正交
五、模糊数学
1、模糊数学基本知识
2、模糊集合
3、模糊关系
4、模糊假言推理
一、不确定性推理
1、不确定性推理含义
不确定性推理:又称不精确推理,是相对于确定性推理而提出来的。指推理中所使用的前提条件、判断是不确定的或者是模糊的情况,因而推理所得出的结论与判断也是不精确的、不确定的或模糊的。
确定性推理的过程,按照必然的因果关系或严格的逻辑推论来进行,是从已知事实出发,通过运用相关知识逐步推出结论的思维过程,获得的推理结论也是严格按照一定的规则予以肯定或否定。
确定性推理是有规律可循的,容易形成完备算法,有满足唯一解的特性,但精确性是暂时的、局部的、相对的,而不确定性是必然的、动态的、永恒的。
2、知识不确定性的来源
研究不确定性推理,首先要研究知识的不确定性。知识的不确定性,用相应的知识表示模式与之对应,以便于推理与计算,还需用适当的方法把知识的不确定性及其程度描述出来。
不确定性有随机性和模糊性两个特性。
知识不确定性来源于:
(1)知识的不完备性:知识内容的不完备包括获取知识观察不充分,设备不精确。知识结构的不完备包括人的认知能力、获取手段的限制,忽略了重要因素。
(2)不协调性:知识内在的矛盾,不协调的程度可以依次为冗余、干扰冲突等允许包容
并蓄,允许折中、调和。
(3)非恒常性:知识随时间变化而变化的特性。
3、不确定推理要解决的基本问题
在专家系统中,不确定性表现在证据、规则和推理三个方面,需要对专家系统中的事实与规则给出不确定性描述,并在此基础上建立不确定性的传递计算方法,因此不确定性知识要解决的问题有表示问题,计算问题,语义解释问题。
(1)表示问题:表示问题指的是采用什么方法描述不确定性,通常有数值表示和非数值的语义表示方法。
在专家系统中的“不确定性”一般有两类:证据的不确定性,知识的不确定性
证据的不确定性:记作命题E,C(E),其中C(E)表示E为真的程度,为动态强度。
证据一般由两个来源:初始证据(针对要求解问题所提供的事实,用户提供),推理证据(依据前面事实推出的若干新情况和判断,计算得到)
知识的不确定性:记作E→H,f(H,E),其中f(H,E)表示知识的不确定性程度,为知识强度或规则强度。
(2)计算问题:主要指不确定性的传播和更新,即获得信息的过程,它是领域专家给出的规则强度和用户给出的原始证据的不确定性的基础上,定义一组函数,求出结论的不确定性度量。
计算问题包括三个方面:不确定性的传递算法,结论不确定性合成,组合证据的不确定性算法。
(3)语义问题:指上述表示和计算的含义
4、不确定性推理方法分类
不确定性推理分为控制法和模型法。
(1)控制法:通过识别领域中引起不确定性的某些特征及相应的控制策略来限制或减少不确定性对系统产生的影响,但没有处理不确定性的统一模型,其效果极大地依赖于控制策略。
(2)模型方法:把不确定证据和不确定的知识分别为某种度量标准对应,并且更新结论不确定性算法,从而建立不确定性推理模式。
在许多不确定性推理的数学方法中,目前常用的主要手段有基于概率的似然推理,基于模糊数学的模糊推理,可信度方法以及人工神经网络算法、遗传算法的计算推理等。
二、主观贝叶斯方法
1、主观贝叶斯方法
主观概率:在许多情况下,同类事件发生的频率不高,甚至很低,无法做概率统计,这时一般是根据观测到数据,凭领域专家的经验给出一些主观上的判断,称为主观概率。
主观信任度:概率一般可以解释为对证据和规则的主观信任度。
2、知识不确定性的表示
知识表示方式:在主观贝叶斯方法中,知识是用产生式规则表示的,具体形式为:IF E THEN(LS,LN) H。其中,(LS,LN)用来表示该知识的知识强度。
(1) LS(充分性度量),表示E对H的支持程度,取值为[0,∞),由专家给出。
![]()
(2)LN(必要性度量),表示![]() E对H的支持程度,即E对H为真的必要性程度,取值范围[0,∞),由专家给出。
E对H的支持程度,即E对H为真的必要性程度,取值范围[0,∞),由专家给出。
![]()
(3)O(X)(几率函数):
![]()
其中,P(X)=0,O(X)=0;P(X)=1,O(X)=+∞,可见O(X)取值[0,+∞)。
(4)O(H|E)为贝叶斯公式的几率似然性形式:
![]()
若 LS=+∞,则证据E对H为真实逻辑充分的。
(5)O(H|![]() E)为贝叶斯必然似然性形式:
E)为贝叶斯必然似然性形式:
![]()
若LN=0,O(H|![]() E)=0,说明
E)=0,说明![]() E为真时,H必然假,E对H是必然的。
E为真时,H必然假,E对H是必然的。
(6)LS性质:
当LS>1时,O(H|E)>O(H),说明E支持H,LS越大,E对H的支持越充分。
当LS→∞时,O(H|E)→∞,由于E的存在,导致H为真。
当LS=1时,O(H|E)=O(H),说明E对H没有影响
当LS<1时,O(H|E) 当LS=0时,E的存在使H为假。 (7)LN性质: 当LN>1时,O(H| 当LN→∞,O(H| 当LN=1时,O(H| 当LN<1时,O(H| 当LN=0时,O(H| (8)LS和LN的关系: 要么一个小于1,一个大于1;要么两个都取1。 证据分为全证据和部分证据。 全证据:所有证据包括所有可能的证据和假设,组成证据E。 部分证据:是证据E的一部分,通常称为观察H。 先验概率是P(E),后验概率是P(E|S)。 (1)若证据E为真,则先验概率等于后验概率等于1,P(E)=P(E|S)=1。 (2)若证据E为假,则先验概率等于后验概率等于0,P(E)=P(E|S)=0。 1975年肖特里非等人在确定性理论的基础上,结合概率论等提出的一种不确定性推理方法。 可信度:根据经验对一个事物或现象为真的相信程度,具有较大主观性和经验性。 C-F模型:基于可信度表示的不确定性推理的基本方法。 知识的不确定性表示:IF E THEN H (CF(H,E)),其中CF(H,E)叫做可信度因子,反映前提条件与结论的联系强度,取值[-1,1],大于0表示支持为真,小于0表示支持为假。 证据的不确定性表示:CF(H,E),当E所对应的证据为真时对H的影响程度。 合取:E=E1 AND E2...En,则CF(E=min{CF(E1),CF(E2},...,CF(En) 析取:E=E1 OR E2...En,则CF(E=max{CF(E1),CF(E2},...,CF(En) 传递:CF(H)=CF(H,E) 合成:假设有知识IF 优点:简洁、直观、容易理解。 缺点:可能导致计算的累计误差,组合规则的顺序不同,也可能会产生不同的结果。 证据理论,也称D-S理论,最早是德姆斯特用一个概率范围而不是单个的概率值去模拟不确定性。 设函数m: 概率分配函数的作用是把Ω的任意一个子集都映射为[0,1]上的一个数m(A)。 另外如果为规定m(A)分给子集中的哪一个变量时,m(A)无法分配。 概率分配函数不是概率,也不必和等于1。 设函数Bel: 例如,Bel({红,黄})=m({红})+m({黄})+m({红,黄}),则Bel又叫做下限函数。 设函数Pl: 似然函数又称为不可驳斥函数或上限函数,表示对A非假的信任度。 (1)空集的信任函数和似然函数均为0,全集Ω的信任函数和似然函数均为1. (2)若 (3) (4) 设m1和m2为两个不同的概率分配函数,正交和m满足: 其中 1965年,扎德提出模糊集合,开创模糊理论。 模糊推理时利用模糊性知识进行的一种不确定性推理。 论域:所讨论的全体对象,用U表示。 元素:论域中每个对象,常用a,b,c表示。 集合:论域中具有某种相同属性的确定的,可以彼此区别的元素的全体,常用A,B表示。 模糊逻辑中,给集合中每一个元素赋予一个介于0和1之间的实数,描述其属于一个集合的强度,该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体构成集合的隶属函数。 隶属度:集合元素对集合的隶属程度,用μ表示,值越大隶属程度越高。 模糊集合表示:用"隶属度/元素"表示,例如: (1)模糊集合相等:当且仅当他们的隶属函数在论域U上恒等时模糊集合相等。 (2)包含:若模糊集合A包含于模糊集合B中,当且仅当对于论域U中所有元素x,恒有 (3)并、交、补: (4)积:设A、B分别为论域U和V上的模糊集合,则 模糊关系:设U和V为论域,U到V上的模糊关系为R,则 模糊矩阵如下图: 模糊关系矩阵乘法中,“×”换min,“+”换max。 模糊产生式规则一般形式:IF E THEN R(CF,λ),其中E和R分别表示模糊条件和模糊结论,CF表示可信度因子,λ表示阈值,指出相应知识何时可被使用。 贴近度:设A,B分别为论域U上的模糊集合,贴近度 参考视频:【人工智能教程】5.1 - 不确定性推理概述_哔哩哔哩_bilibili 参考书籍:《人工智能原理》丁世飞![]() E)>O(H),说明
E)>O(H),说明![]() E支持H,由于E的不出现,增大H为真的概率。
E支持H,由于E的不出现,增大H为真的概率。![]() E)→∞,说明
E)→∞,说明![]() E的存在导致H为真。
E的存在导致H为真。![]() E)=O(H),
E)=O(H),![]() E对H没有影响。
E对H没有影响。![]() E)
E)![]() E)=0,
E)=0,![]() E的存在使H为假。
E的存在使H为假。3、证据
4、不确定性的更新
![]()
![]()
三、可信度方法
1、可信度模型
2、性质
![]() max{0,CF(E)}
max{0,CF(E)}![]() THEN H (CF(H,
THEN H (CF(H,![]() ))和IF
))和IF ![]() THEN H (CF(H,
THEN H (CF(H,![]() )),首先对每一条知识分别求CF(H),然后根据下面公式进行合成。
)),首先对每一条知识分别求CF(H),然后根据下面公式进行合成。 3、可信度方法特点
四、证据理论
1、概率分配函数
![]() →[0,1],且满足
→[0,1],且满足![]() ,
,![]() ,则称m为
,则称m为![]() 上的概率分配函数,m(A)为基本概率数,表示依据当前的环境对假设集A的信任程度。
上的概率分配函数,m(A)为基本概率数,表示依据当前的环境对假设集A的信任程度。2、信任函数
![]() →[0,1],对任意A
→[0,1],对任意A![]() Ω有,
Ω有,![]() ,Bel(A)为当前环境下,对假设集A的信任程度,其值为A的所有子集的基本概率之和,为对A的总信任度。
,Bel(A)为当前环境下,对假设集A的信任程度,其值为A的所有子集的基本概率之和,为对A的总信任度。3、似然函数
![]() →[0,1],对任意A
→[0,1],对任意A![]() Ω有,
Ω有,![]() ,其中
,其中![]() 。
。4、性质
![]() ,则
,则![]()
![]()
![]()
5、正交
![]() ,
,![]()
![]()
五、模糊数学
1、模糊数学基本知识
2、模糊集合
![]() ,其中“+”不是求和的意思,只是一种记法,另外扎德又进行简化
,其中“+”不是求和的意思,只是一种记法,另外扎德又进行简化![]() 。
。![]() 。
。![]()
![]()
![]()
![]()
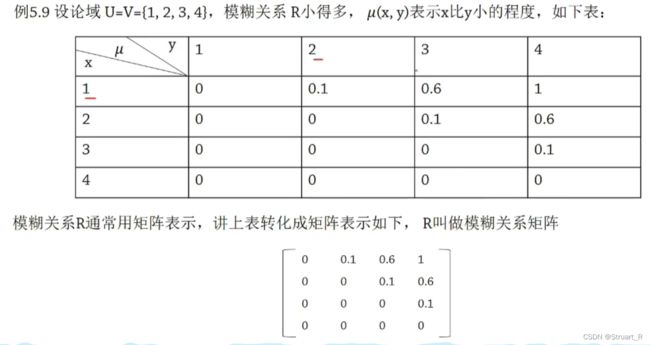
3、模糊关系
![]() 代表有序对
代表有序对4、模糊假言推理
![]() 。其中,
。其中,![]() ,
,![]() 。
。