复数

---

---

复数

视频地址：复数

虚数$i$

虚数 $i$是一个数学符号，用于表示实数平方根的概念扩展。虚数 $i$定义为：

$i=\sqrt{-1}$

在此定义下，$i$的平方是 -1：

$i^2=-1$

虚数是复数理论的基础，复数是具有实部和虚部的数字。任何复数都可以写成 $a+bi$的形式，其中 $a$和 $b$是实数，$i$是虚数单位。

几何解释

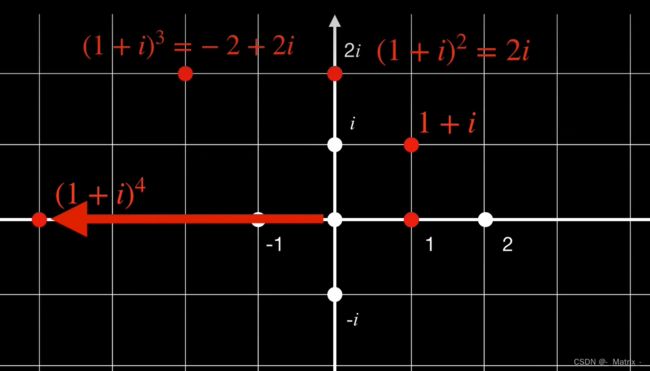
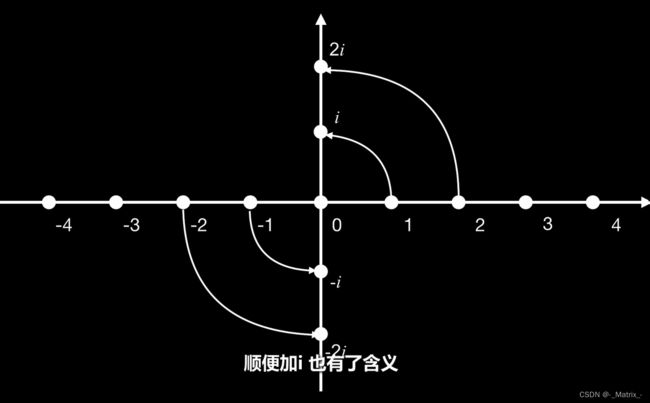
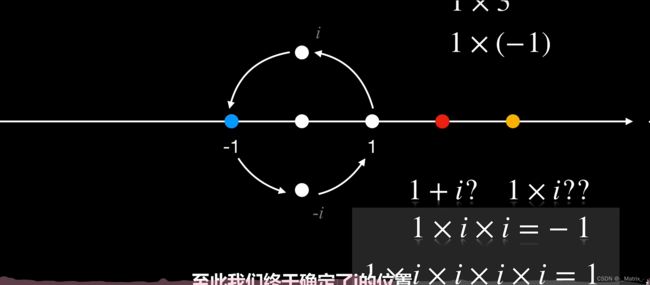
在复平面上，虚数 $i$ 可以表示为逆时针旋转$90°$的操作。这一几何解释有助于直观地理解复数的运算，特别是乘法和除法。

复数

复数是一种数学表达形式，可以表示为实数和虚数的组合。每个复数 $z$都可以表示为

$z=a+bi$

其中 $a$和 $b$是实数，$i$是虚数单位，满足 $i^2=-1$。

复数的性质

1. 加法和减法：复数的加法和减法与实数的运算类似，只需分别对实部和虚部进行运算。
   复数平面的特性:复数的加法和减法可以通过向量的几何加法和减法来可视化.
   

2. 乘法：复数的乘法可以通过分配律展开，然后使用 $i^2=-1$来化简。
   复数平面的特性:复数的乘法和除法可以通过角度和模长的乘法和除法来解释。复数乘法相当于旋转和拉伸操作。
   

3. 共轭：复数的共轭是实部不变，虚部的符号改变的复数。对于复数 $z=a+bi$，其共轭为 $\bar{z}=a-bi$。复数平面的特性:复数的共轭是关于实轴的对称点。

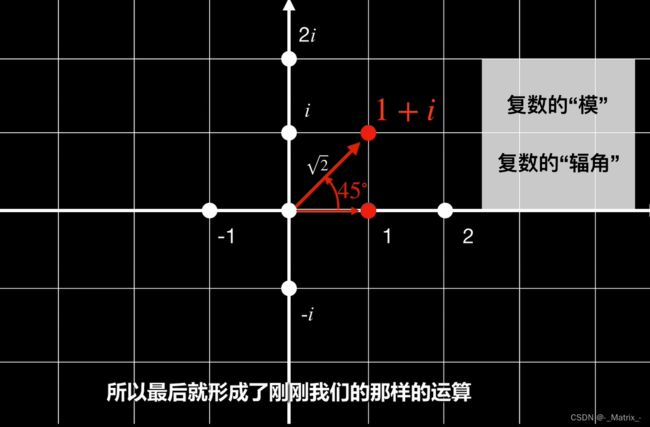
4. 模：复数的模是其到复平面原点的距离，用 $|z|$表示，计算公式为 $|z|=\sqrt{a^2+b^2}$。
   复数平面的特性:复数的模是原点到复数平面上的点的距离。
   

5. 幅角：复数的幅角是从正实轴逆时针旋转到该复数所需的角度。复数的幅角是从正实轴到复数所在的线段的角度。

6. 除法：复数的除法可以通过乘以除数的共轭和调整模来实现。

7. 指数和对数形式：复数可以使用欧拉公式以指数形式表示，例如 $e^{ix}=\cos x+i\sin x$。

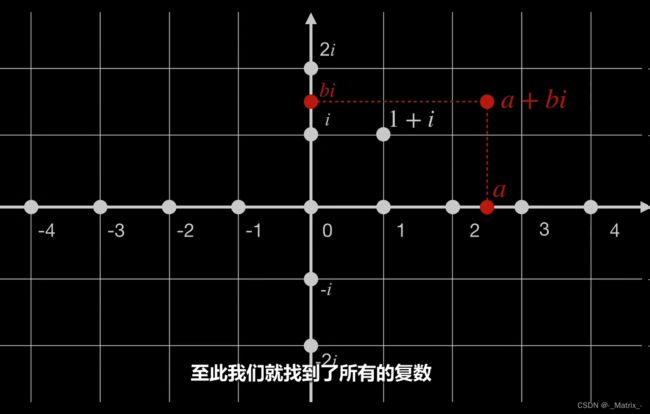
复数平面是一种二维坐标系统，用于表示和可视化复数。在复数平面上，水平轴（通常称为x轴）代表复数的实部，而垂直轴（通常称为y轴）代表复数的虚部。

每个复数 $z=a+bi$都可以表示为复数平面上的一个点，其中实部 $a$为点的x坐标，虚部 $b$为点的y坐标。

复数的加法

复数加法是将两个复数相加的过程。对于两个复数 $z=a+bi$ 和 $w=c+di$，它们的和可以通过以下简单步骤计算：

1. 加实部

将两个复数的实部相加：

$\text{实部之和}=a+c$

2. 加虚部

将两个复数的虚部相加：

$\text{虚部之和}=b+d$

3. 组合实部和虚部

将实部和虚部组合在一起，得到最终结果：

$z+w=(a+c)+(b+d)i$

复数加法的几何解释

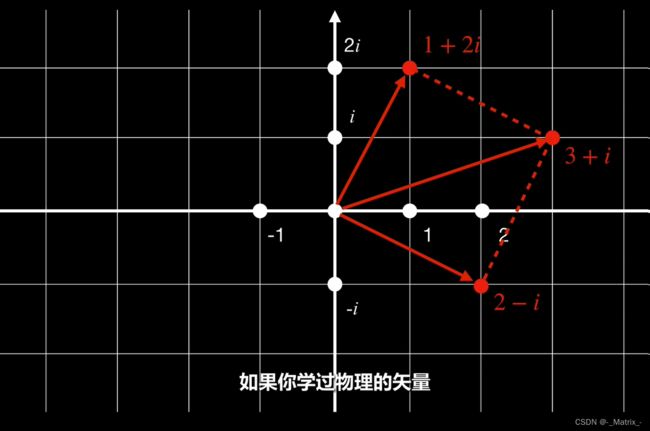
在复数平面上，复数加法可以通过向量的几何加法来解释。你可以将复数 $z$ 和 $w$ 分别看作复数平面上的两个点，或者原点到这两个点的两个向量。然后，将这两个向量头尾相连，并绘制从原点到最后一个向量的尾部的新向量。这个新向量就表示复数的和。

总结

复数加法是一种直观且容易计算的运算，它通过将实部和虚部分别相加来实现。在复数平面上，这个操作具有直观的几何解释，可以通过向量加法来可视化。

复数减法

复数减法是将两个复数相减的过程。如果有两个复数 $z=a+bi$ 和 $w=c+di$，它们的差可以通过以下简单步骤计算：

1. 减实部

将两个复数的实部相减：

$\text{实部之差}=a-c$

2. 减虚部

将两个复数的虚部相减：

$\text{虚部之差}=b-d$

3. 组合实部和虚部

将实部和虚部组合在一起，得到最终结果：

$z-w=(a-c)+(b-d)i$

复数减法的几何解释

在复数平面上，复数减法也可以通过向量的几何减法来解释。你可以将复数 $z$ 和 $w$ 分别看作复数平面上的两个点，或者原点到这两个点的两个向量。然后，将 $w$ 的向量反向，并与 $z$ 的向量头尾相连。新形成的向量就表示复数的差。

总结

复数减法是一种直观且容易计算的运算，可以通过将实部和虚部分别相减来实现。在复数平面上，这个操作具有直观的几何解释，并可以通过向量减法来可视化。

复数乘法

复数乘法涉及将两个复数相乘以形成一个新的复数。设有两个复数 $z=a+bi$ 和 $w=c+di$，它们的乘积可以通过以下步骤计算：

1. 展开乘法

将两个复数的乘法展开，就像对多项式进行乘法一样：

$(a+bi)(c+di)=ac+adi+bci+bd{i}^2$

2. 使用 $i^2=-1$

我们知道虚数单位 $i$ 的平方等于 -1，所以我们可以将 $i^2$ 替换为 -1：

$bd{i}^2=-bd$

3. 合并实部和虚部

将实部和虚部组合在一起：

$(a+bi)(c+di)=(ac-bd)+(ad+bc)i$

复数乘法的几何解释

在复数平面上，复数乘法具有有趣的几何解释。复数的模表示其与原点的距离，而幅角表示与正实轴的角度。复数乘法相当于将这两个复数的模相乘，并将它们的幅角相加。

总结

复数乘法可以通过简单的实数运算计算，并在许多数学和工程应用中都有用处。它在复数平面上的几何解释也为理解复数的性质和行为提供了直观的洞察。

复数除法

复数除法是将一个复数除以另一个复数的过程。设有两个复数 $z=a+bi$ 和 $w=c+di$，我们想求解 $\frac{z}{w}$。

这个过程可以通过以下步骤完成：

1. 求除数的共轭

找到 $w$ 的共轭 $\bar{w}=c-di$。

2. 两侧同乘共轭

将分子和分母都乘以共轭 $\bar{w}$，得到：

$\frac{z}{w}\times \frac{\bar{w}}{\bar{w}}=\frac{z\cdot \bar{w}}{w\cdot \bar{w}}$

3. 展开乘法

展开乘法，得到：

$\frac{(a+bi)(c-di)}{(c+di)(c-di)}$

4. 计算分母

分母 $(c+di)(c-di)$ 为 $c^2+d^2$，因为虚部中的 $di\times (-di)$ 将消掉。

5. 计算分子

分子部分可以通过乘法展开，得到：

$(a+bi)(c-di)=ac-adi+bci+bd{i}^2=ac-adi+bci-bd$

6. 合并实部和虚部

将实部和虚部组合在一起，得到最终结果：

$\frac{z}{w}=\frac{ac-bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i$

通过这个过程，我们可以将复数除法转化为实数的基本运算，使其更易于计算和理解。在复数平面上，这个操作相当于旋转和缩放，因为复数除法改变了复数的模和幅角。

模长和幅角表示 加减乘除

反正切函数

$\arctan$ 是反正切函数的表示，也被称为正切的反函数或反正切。如果 $y=\tan (x)$，那么 $\arctan (y)=x$。

反正切函数将一个实数值映射到 $-\frac{\pi }{2}$ 到 $\frac{\pi }{2}$ 的角度，表示那个角度的正切值与给定的实数相等。

例如，$\arctan (1)=\frac{\pi }{4}$，因为 $\tan \left(\frac{\pi }{4}\right)=1$。

在计算中，你通常可以使用编程语言或数学软件中的反正切函数来计算这个值。在许多环境中，还有一个叫做 $\text{atan2}(y,x)$ 的函数，它返回通过 $y/x$ 给定的斜率对应的角度，并在确定正确象限方面更精确。这在复数运算中特别有用，因为你可以使用 $\text{atan2}(b,a)$ 来计算复数 $a+bi$ 的幅角。

代码实现

是的，C++标准库中包括了 atan2(y, x) 函数，该函数可用于计算点 (x, y) 与X轴之间的角度。你可以通过包括头文件 来使用这个函数。

下面是一个例子，展示了如何使用 atan2(y, x)：

#include 
#include 

int main() {
    double y = 1.0;
    double x = 1.0;
    double result = atan2(y, x);
    std::cout << "The angle is: " << result << " radians\n";
    return 0;
}

atan2(y, x) 函数的结果是以弧度表示的，如果你想要将其转换为度，你可以使用 result * 180 / M_PI。在C++中，M_PI 是π的一个常见定义，但并非所有编译器都定义了它。如果你的编译器没有定义 M_PI，你可以自己定义，如 const double M_PI = 3.14159265358979323846;。

复数可以通过模长和幅角来表示，这被称为复数的极坐标形式。对于复数 $z=a+bi$，我们可以使用以下方法将其表示为极坐标形式。

模长（Magnitude）

复数的模长，也称为绝对值，是复数与原点之间在复数平面上的距离。它可以通过以下公式计算：

$r=|z|=\sqrt{a^2+b^2}$

幅角（Argument）

复数的幅角，也称为角度，是复数与正实轴之间的角度。它通常用希腊字母 $\theta$ 表示，并可以通过以下公式计算：

$\theta =\arctan \left(\frac{b}{a}\right)$

极坐标形式

结合模长和幅角，我们可以将复数表示为极坐标形式：

$z=r(\cos \theta +i\sin \theta )$

我们可以展开它并找到其实部和虚部。

实部

实部由模长与余弦部分的乘积给出：

$a=r\cos \theta$

虚部

虚部由模长与正弦部分的乘积给出：

$b=r\sin \theta$

标准形式

结合实部和虚部，我们可以得到复数的标准形式：

$z=a+bi=r\cos \theta +r\sin \theta i$

例子

例如，如果 $ r = 2 $ 并且 $\theta =\frac{\pi }{4}$，那么：

$z=2\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right)=\sqrt{2}+\sqrt{2}i$

Euler公式

使用Euler公式，极坐标形式可以进一步表示为：

$z=r\cdot e^{i\theta }$

总结

模长和幅角提供了一种表示复数的有用方法，它捕捉了复数在复数平面上的几何特性。极坐标形式在许多数学和工程应用中都很有用，特别是在处理复数乘法和除法时，因为这些操作可以简化为模长的乘法和除法，以及幅角的加法和减法。

复数加法

复数加法在极坐标形式（模长和幅角）下并不像乘法和除法那样直观。不过，你仍然可以使用以下步骤进行计算：

设有两个复数 $z=r_1(\cos {\theta }_1+i\sin {\theta }_1)$ 和 $w=r_2(\cos {\theta }_2+i\sin {\theta }_2)$，你想要找到它们的和。

1. 转换到标准形式：
   $z=r_1\cos {\theta }_1+r_1\sin {\theta }_{1}i$
   $w=r_2\cos {\theta }_2+r_2\sin {\theta }_{2}i$

2. 相加：
   $z+w=(r_1\cos {\theta }_1+r_2\cos {\theta }_2)+(r_1\sin {\theta }_1+r_2\sin {\theta }_2)i$

3. 找到结果的模长和幅角：
   你可以使用下面的公式找到复数的模长：
   $r=\sqrt{{(r_1\cos {\theta }_1+r_2\cos {\theta }_2)}^2+{(r_1\sin {\theta }_1+r_2\sin {\theta }_2)}^2}$
   并使用下面的公式找到幅角（请注意，你可能需要使用四象限反正切函数来正确确定角度）：
   $\theta =\arctan \frac{r_1\sin {\theta }_1+r_2\sin {\theta }_2}{r_1\cos {\theta }_1+r_2\cos {\theta }_2}$

结果

因此，两个复数的和的极坐标形式是：
$z+w=r(\cos \theta +i\sin \theta )$

尽管在极坐标形式下进行复数加法略显复杂，但该方法在涉及复杂计算的问题中仍可能有用。

复数减法

复数减法在极坐标形式（使用模长和幅角）下也是可能的，但与加法类似，它不如乘法和除法直观。以下是如何使用模长和幅角进行复数减法的步骤：

设有两个复数 $z=r_1(\cos {\theta }_1+i\sin {\theta }_1)$ 和 $w=r_2(\cos {\theta }_2+i\sin {\theta }_2)$，你想要找到它们的差 $z-w$。

1. 转换到标准形式：
   $z=r_1\cos {\theta }_1+r_1\sin {\theta }_{1}i$
   $w=r_2\cos {\theta }_2+r_2\sin {\theta }_{2}i$

2. 相减：
   $z-w=(r_1\cos {\theta }_1-r_2\cos {\theta }_2)+(r_1\sin {\theta }_1-r_2\sin {\theta }_2)i$

3. 找到结果的模长和幅角：
   你可以使用下面的公式找到复数的模长：
   $r=\sqrt{{(r_1\cos {\theta }_1-r_2\cos {\theta }_2)}^2+{(r_1\sin {\theta }_1-r_2\sin {\theta }_2)}^2}$
   并使用下面的公式找到幅角（请注意，你可能需要使用四象限反正切函数来正确确定角度）：
   $\theta =\arctan \frac{r_1\sin {\theta }_1-r_2\sin {\theta }_2}{r_1\cos {\theta }_1-r_2\cos {\theta }_2}$

结果

因此，两个复数的差的极坐标形式是：
$z-w=r(\cos \theta +i\sin \theta )$

在处理涉及多个复数的复杂问题时，此方法可能仍然有用，尽管它在极坐标形式下并不像乘法和除法那么直观。

复数乘法

使用模长和幅角来表示复数时，复数相乘变得非常直观和方便。

设有两个复数 $z=r_1(\cos {\theta }_1+i\sin {\theta }_1)$ 和 $w=r_2(\cos {\theta }_2+i\sin {\theta }_2)$，我们想要找到它们的乘积。

模长

两个复数的乘积的模长是它们各自模长的乘积：

$r=r_1\cdot r_2$

幅角

两个复数的乘积的幅角是它们各自幅角的和：

$\theta ={\theta }_1+{\theta }_2$

结果

因此，两个复数的乘积可以表示为：

$z\cdot w=r(\cos \theta +i\sin \theta )=r_1{r}_2(\cos ({\theta }_1+{\theta }_2)+i\sin ({\theta }_1+{\theta }_2))$

例子

例如，设 $z=2(\cos \frac{\pi }{4}+i\sin \frac{\pi }{4})$ 和 $w=3(\cos \frac{\pi }{3}+i\sin \frac{\pi }{3})$，那么

$z\cdot w=2\cdot 3(\cos (\frac{\pi }{4}+\frac{\pi }{3})+i\sin (\frac{\pi }{4}+\frac{\pi }{3}))=6(\cos \frac{7\pi }{12}+i\sin \frac{7\pi }{12})$

使用模长和幅角来进行复数乘法使运算变得更直观，特别是在涉及复数乘积的更复杂表达式中。它还强调了复数乘法的几何意义，即将两个复数的模长相乘，并将它们的幅角相加。

复数除法

使用模长和幅角表示复数时，复数除法变得相当直观。假设你有两个复数 $z=r_1(\cos {\theta }_1+i\sin {\theta }_1)$ 和 $w=r_2(\cos {\theta }_2+i\sin {\theta }_2)$，并且你想要计算 $\frac{z}{w}$。

模长

两个复数的商的模长是它们各自模长的商：

$r=\frac{r_1}{r_2}$

幅角

两个复数的商的幅角是第一个复数的幅角减去第二个复数的幅角：

$\theta ={\theta }_1-{\theta }_2$

结果

因此，两个复数的商可以表示为：

$\frac{z}{w}=r(\cos \theta +i\sin \theta )=\frac{r_1}{r_2}(\cos ({\theta }_1-{\theta }_2)+i\sin ({\theta }_1-{\theta }_2))$

例子

例如，设 $z=2(\cos \frac{\pi }{4}+i\sin \frac{\pi }{4})$ 和 $w=3(\cos \frac{\pi }{3}+i\sin \frac{\pi }{3})$，那么

$\frac{z}{w}=\frac{2}{3}(\cos (\frac{\pi }{4}-\frac{\pi }{3})+i\sin (\frac{\pi }{4}-\frac{\pi }{3}))=\frac{2}{3}(\cos \frac{-\pi }{12}+i\sin \frac{-\pi }{12})$

使用模长和幅角进行复数除法使运算更为直观，特别是在涉及复数商的更复杂表达式中。它还强调了复数除法的几何意义，即将两个复数的模长相除，并将第一个复数的幅角减去第二个复数的幅角。