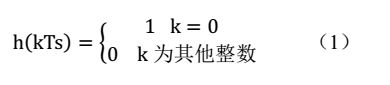信息与通信工程面试准备——信号与系统｜10:23

8月16日 23:21

目录

​编辑

1. 调制的作用

2. 放大器与振荡器的作用和区别

工作原理

输出信号

应用

反馈方式

设计复杂度

装置性质

3. 信号与系统：三大变换之间的关系？

4. 无码间串扰的条件

5. 冲激函数的作用？

研究的意义？

6. 系统用什么来表示？

系统的定义

系统表示方法

7. 滤波器的分类

7.1 按信号处理的方式

7.2 按通频带分类

7.3 按元件分类

8. ofdm cdma

8.1 CDMA(码分多址)

8.2 OFDM(正交频分复用) 

OFDM的发送、接收过程

OFDM的主要优点

9. 香农公式

10. 信源编码与信道编码

---

1. 调制的作用

提高无线通信时的无线辐射效率；

把多个基带信号分别搬移到不同的载频处，实现信道的多路复用，提高信道利用率；

在无线传输中，调制可以扩展信号带宽，从而提高系统抗干扰能力。

2. 放大器与振荡器的作用和区别

　振荡器（Oscillator）是一种电路，可以产生一定频率和振幅的周期性信号。振荡器的作用是将直流电源的电能转换为交流电能，产生固定频率的交流信号，是无线通讯、数字电路、控制系统等领域中不可或缺的基础电路之一。振荡器的主要应用包括：信号发生器、时钟发生器、扫描电子显微镜、激光、无线电、通讯等。

振荡器与放大器的区别：

工作原理

　　1.工作原理不同：放大器是一种电路，其主要作用是将输入信号放大到一定的幅度，输出到负载上，而振荡器则是一种能够自主产生信号的电路。

输出信号

　　2.输出信号不同：放大器的输出信号与输入信号有一定的相似性，而振荡器则是产生一个完全不同于输入信号的输出信号。

应用

　　3.应用不同：放大器主要用于放大信号，如音频放大器、功率放大器等，而振荡器主要用于产生信号，如无线电发射机、振铃电路、时钟电路等。

反馈方式

　　4.反馈方式不同：放大器的反馈方式通常是负反馈，而振荡器则是正反馈。

设计复杂度

　　5.设计复杂度不同：振荡器的设计比放大器更加复杂，需要满足的条件也更多，因为振荡器需要产生一定的频率和振幅，而且还需要满足一定的稳定性和可靠性。

装置性质

        6.装置：振荡器是一种能量转换装置，将直流电能转换为具有一定频率的交流电能。放大器则是一种能把输入信号的电压或功率放大的装置，由电子管或晶体管、电源变压器和其他电器元件组成。

　　总之，振荡器和放大器虽然都是电路，但是其工作原理、输出信号、应用和设计复杂度等方面都有很大的不同。在实际应用中，需要根据具体的需求来选择合适的电路。

3. 信号与系统：三大变换之间的关系？

        傅立叶变换即FT，又称之为连续时间下的傅立叶变换，DTFT离散时间傅立叶变换是FT的离散形式，为了让计算机求解傅立叶变换，我们不得不限制一个有限的处理区间，因此有了DFT离散傅立叶变换。所以DFT主要是服务于计算机。而经典算法FFT快速傅立叶变换则是通过分治的思想，将DFT的复杂度由O(n2)降至对数数量级。所以FFT是DFT的一种加速算法。

        傅立叶变换是最基本得变换，由傅立叶级数推导出。傅立叶级数只适用于周期信号，把非周期信号看成周期T趋于无穷的周期信号，就推导出傅里叶变换，能很好的处理非周期信号的频谱。但是傅立叶变换的弱点是必须原信号必须绝对可积，因此适用范围不广。

        拉普拉斯变换是傅立叶变换的推广，傅立叶变换不适用于指数级增长的函数，而拉氏变换相当于是带有一个指数收敛因子的傅立叶变换，把频域推广到复频域，能分析的信号更广。然而缺点是从拉普拉斯变换的式子中，只能看到变量s，没有频率f的概念，要看幅频响应和相频响应，还得令s=j2πf.

        Z变换的本质是离散时间傅立叶变换（DTFT），如果说拉普拉斯变换专门分析模拟信号，那Z变换就是专门分析数字信号，Z变换可以把离散卷积变成多项式乘法，对离散数字系统能发挥很好的作用。Z变换看系统频率响应，就是令Z在复频域的单位圆上跑一圈，即Z=e^(j2πf)，即可得到频率响应。由于傅里叶变换的特性“时域离散，则频域周期”，因此离散信号的频谱必定是周期的，就是以这个单位圆为周期，Z在单位圆上不停的绕圈，就是周期重复。单位圆0°位置是实际频率0HZ，单位圆180度的实际频率就是采样频率的一般为fs/2.

4. 无码间串扰的条件

        只要基带传输系统的冲激响应波形h(t)仅在本码元的抽样时刻上有最大值，并在其他码元的抽样时刻上均为0，则可消除码间串扰。即，若对h(t)在时刻t=kTs（这里假设信道和接收滤波器所造成的延迟t0=0）抽样，则应有下式成立：

        上式（1）称为无码间串扰的时域条件。即，若h(t)的抽样值除了在t=0时不为零外，在其他所有抽样点上均为零，就不存在码间串扰。

5. 冲激函数的作用？

描述间断点导数；

具有取样特性；

通过冲激函数表示复杂的信号，简化研究，减少计算复杂信号频谱的难度。

研究的意义？

        冲激函数是个奇异函数，它是对强度极大、作用时间极短暂且积分有限的一类理想化数学模型。冲激函数可用于对连续信号进行线性表达，也可用于求解线性非时变系统的零状态响应。

        对冲激函数求导可得到冲激偶函数，单位冲激偶是这样的一种函数：当 t从负值趋于0时，它是一个强度为无限大的正的冲激函数，当t从正值趋于0时，它是一个强度为无限大的负的冲激函数。

        冲激函数可用于信号处理，通过冲激函数来表示复杂的信号，可以简化对复杂信号的一些特性的研究。冲激函数及其延时冲激函数的线性组合来表示或逼近，再利用系统的迭加原理，可以通过简单的信号如单位冲激函数的频谱，以及频域特性来讨论比较复杂信号的频谱。从而减少计算复杂信号频谱的难度。

6. 系统用什么来表示？

系统的定义

        系统是指由相互作用和依赖的若干单元组合而成的、具有特定功能的有机整体。例如，一个手机打电话给另一个手机，要实现这个功能需要发送端手机、基站、接收端手机、电磁波等物质，这些物质就是系统的组成部分，缺一不可。

系统表示方法

代数表示

微（差）分方程

常微分方程

系统函数

系统框图

信号流程图

状态方程

波特图表示

7. 滤波器的分类

7.1 按信号处理的方式

按所处理的信号分为模拟滤波器和数字滤波器两种。

7.2 按通频带分类

按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。

1、低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声；

2、高通滤波器：它允许信号中的高频分量通过，抑制低频或直流分量；

3、带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪声；

4、带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。

7.3 按元件分类

按元件分类，滤波器可分为：有源滤波器、无源滤波器、陶瓷滤波器、晶体滤波器、机械滤波器、锁相环滤波器、开关电容滤波器等。

---

除此之外，还有一些特殊滤波器，如满足一定频响特性、相移特性的特殊滤波器，例如，线性相移滤波器、时延滤波器、音响中的计杈网络滤波器、电视机中的中放声表面波滤波器等。

按通频带分类，有源滤波器可分为：低通滤波器（LPF）、高通滤波器（HPF）、带通滤波器（BPF）、带阻滤波器（BEF）等。

按通带滤波特性分类，有源滤波器可分为：最大平坦型（巴特沃思型）滤波器、等波纹型（切比雪夫型）滤波器、线性相移型（贝塞尔型）滤波器等。

按运放电路的构成分类，有源滤波器可分为：无限增益单反馈环型滤波器、无限增益多反馈环型滤波器、压控电源型滤波器、负阻变换器型滤波器、回转器型滤波器等。

8. ofdm cdma

CDMA与OFDM之技术比较 - 通信新闻 - 电子发烧友网

8.1 CDMA(码分多址)

        CDMA常称为码分多址，是一种无线通信技术。每个手机用户可在同一时间使用同样的频带进行通信。由于各用户使用经过特殊挑选的不同码型，因此不会造成干扰。CDMA最初是用于军事通信，因为这种系统发送的信号有很强的抗干扰能力，而且不易被敌人发现。CDMA现在已广泛使用在民用的移动通信中。采用CDMA可提高通信的话音质量和数据传输的可靠性，减少干扰对通信的影响，降低手机的平均发射功率。

        在CDMA中，每发送一个二进制数字位需要发送m 比特二进制数字序列，称为码片。为了简单起见，我们设m为8。

        使用CDMA的每一个手机被指派一个惟一的8位码片。一个站如果要发送比特1，则发送它自己的8位码片序列。如果要发送比特0，则发送该码片序列的二进制反码。例如，指派给手机S的8 bit码片序列是00011011。当S发送比特1时，它就发送序列00011011，而当S发送比特0时，就发送11100100。为了方便，我们以后将码片中的0写为-1，将1写为+1。因此手机S的码片序列是(-1 –1 –1 +1 +1 –1 +1 +1)。

假设系统中有4个手机用户进行CDMA通信，给这4个手机指派的码片序列分别为：

E1: (-1 –1 –1  +1  +1 –1  +1 +1)

E2: (-1 –1  +1  -1  +1  +1  +1 -1)

E3: (-1  +1 –1  +1  +1  +1  -1 -1)

E4: (-1  +1 –1  -1  -1 –1  +1 -1)

设码片序列S和T分别为(s1 s2 s3 s4 s5 s6 s7 s8) 和(t1 t2 t3 t4 t5 t6 t7 t8)，有数学公式

(s1*t1 + s2*t2 + s3*t3 + s4*t4 + s5*t5 + s6*t6 + s7*t7 + s8*t8 ) / 8                                 (3-1)

公式(3-1)称为S和T的规格化内积。

我们发现该系统的一个重要特点就是给每一个手机指派的码片序列不仅各不相同，并且互相的规格化内积为0。

不仅如此，一个手机和其他各手机码片的反码的规格化内积也为0。另外一点也很重要，我们可以验证码片E1、E2、E3和E4和各自自身的规格化内积，即：

(s1*s1 + s2*s2 + s3*s3 + s4*s4 + s5*s5 + s6*s6 + s7*s7 + s8*s8) / 8 = +1                     (3-2)

而码片E1、E2、E3和E4和各自码片的反码的规格化内积等于 –1。

现在这4个手机用户都在相互通信，他们发送的是自己的码片序列(相当于发送比特1)，或码片序列的二进制反码(相当于发送比特0)，或什么也不发送(相当于没有数据发送)。

假定有一个手机T要接收手机S发送的数据。手机T就必须知道手机S所特有的码片序列。手机T使用它得到的码片序列S与接收到的未知信号进行求内积的运算。手机T接收到的信号是各个手机发送的码片序列之和。根据上面的公式(3-1)和(3-2)，再根据叠加原理(假定各种信号到达接收端是叠加的关系)，那么求内积得到的结果是：所有其他手机的信号都被过滤掉(其内积的相关项都是0)，而只剩下手机S发送的信号。当手机S发送比特1时，由手机T计算内积的结果是+1，当手机S发送比特0时，内积的结果是-1。

例如手机4事先知道手机1，2和3的码片序列分别E1、E2和E3，手机4 收到码片序列 (-1 -3 +1 -1 +1 -1 +3 +1)后分别与E1、E2和E3作规格化内积运算，得到+1、+1和-1，手机4由此推知手机1、2和3分别发送了1，1，0。

8.2 OFDM(正交频分复用) 

        OFDM（正交频分复用）是一种无线环境下的高速传输技术，适合在多径传播和多普勒频移的无线移动信道中传输高速数据。它能有效对抗多径效应，消除符号间干扰，对抗频率选择性衰落，而且信道利用率高。OFDM技术先后被欧洲数字音频广播（DAB）、欧洲数字视频广播（DVB）、HIPERLAN和IEEE802.11无线局域网等系统采用。

        OFDM是一种高效的数据传输方式，其基本思想是在频域内将给定信道分成许多正交子信道，在每个子信道上使用一个子载波进行调制，并且各子载波并行传输。这样，尽管总的信道是非平坦的，具有频率选择性，但是每个子信道是相对平坦的，在每个子信道上进行的是窄带传输，信号带宽小于信道的相应带宽，因此就可以大大消除信号波形间的干扰。OFDM相对于一般的多载波传输的不同之处是它允许子载波频谱部分重叠，只要满足子载波间相互正交，则可以从混叠的子子载波上分离出数据信号。由于OFDM允许子载波频谱混跌，其频谱效率大大提高，因而是一种高效的调制方式。

        OFDM技术在20世纪60年代中期被首次提出，但在之后相当长的一段时间，OFDM技术一直没有形成大规模的应用。当时OFDM技术的发展遇到了很多似乎难于解决的问题。首先，OFDM要求各个子载波之间相互正交，尽管理论上发现采用快速傅立叶变换（FFT）可以很好地实现这种调制方式，但实际上，如此复杂的实时傅立叶变换设备在当时是根本无法完成的。此外，发射机和接收机振荡器的稳定性以及射频功率放大器的线性要求等因素也都是OFDM技术实现的制约条件。

        20世纪80年代以来，大规模集成电路技术的发展解决了FFT的实现问题，随着DSP芯片技术的发展，格栅编码（TrellisCode）技术、软判决技术（SoftDecision）、信道自适应技术等的应用，OFDM技术开始从理论向实际应用转化。OFDM技术凭借其固有的对时延扩展较强的抵抗力和较高的频谱效率两大优势迅速成为研究的焦点并被多个国际规范采用，如欧洲的数字音频广播、数字视频广播和IEEE的无线局域网标准802.11a。

OFDM的发送、接收过程

        在发送端，发送数据在频域进行编码映射，经过串并变换后做IFFT运算变换到时域：

        经IFFT后，频域信号调制到了各个正交的子载波上，完成了正交频分复用。每个OFDM码元前加上保护间隔，如果保护间隔大于最大时延扩展，则所有时延小于保护间隔的多径信号将不会延伸到下一个码元期间，因而有效地消除了码间串扰。OFDM信号还要经加窗函数以降低带外信号的功率，经低通滤波后调制到主载频发射到信道。

        接收端的处理过程与发射端相反：信道出来的信号先经过主载频解调，低通滤波 A/D转换及串并变换后，再进行FFT得到一个符号的数据。对所得数据进行均衡，以校正信道失真。然后进行译码判决和并串变换，恢复出原始的二元数据序列。

OFDM的主要优点

1. 可以有效克服ISI，适用于多径环境和衰落信道中的高速数据传输。

2. 信道利用率很高，这一点在频谱资源有限的无线环境中尤为重要。当子载波个数很大时，系统的频谱利用率趋于2Baud/Hz。

3. 通过各个子载波的联合编码，可具有很强的抗衰落能力。

4. 可以选用基于IFFT/FFT的OFDM实现方法。

5. 适合高速数据传输。

        OFDM自适应调制机制使不同的子载波可以按照信道情况和噪音背景的不同使用不同的调制方式。当信道条件好的时候，采用效率高的调制方式。当信道条件差的时候，采用抗干扰能力强的调制方式。再有，OFDM加载算法的采用，使系统可以把更多的数据集中放在条件好的信道上以高速率进行传送。
　　

9. 香农公式

10. 信源编码与信道编码

        信源编码：一是通过某种压缩编码技术减少码元数目以降低码元速率，提高信息传输的有效性；二是完成A/D转换，实现模拟信号的数字化。信源译码是信源编码的逆过程。(是一种压缩编码)

        信道编码：发送端信道编码器对传输的码元按照一定的规则加入保护成分（监督码元），接收端信道译码器按照相应的逆规则进行解码，从中发现错误或纠正错误，以提高通信系统的可靠性。（冗余编码）。

​​​​​​​