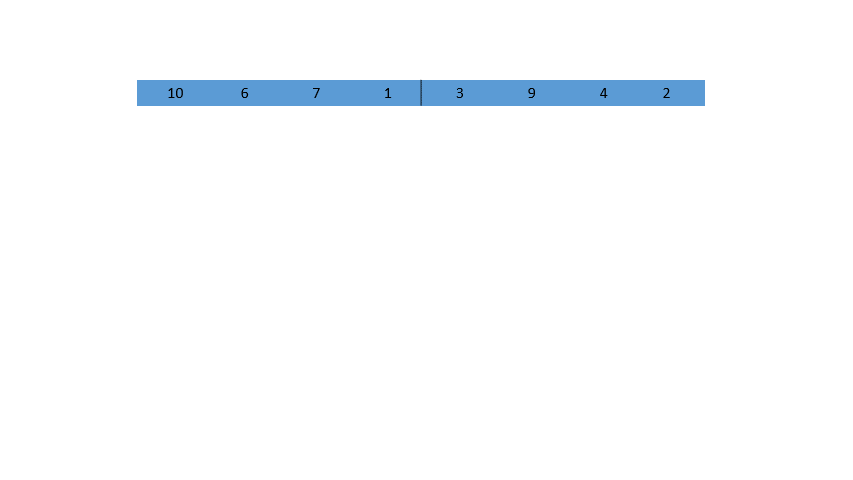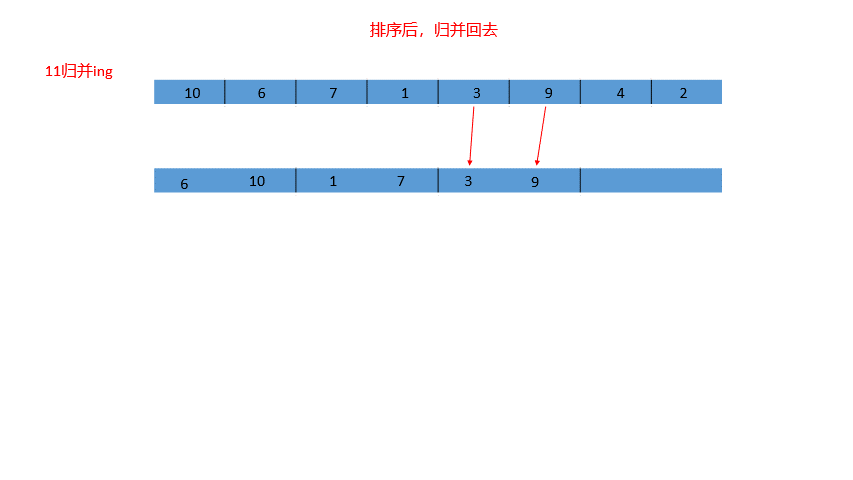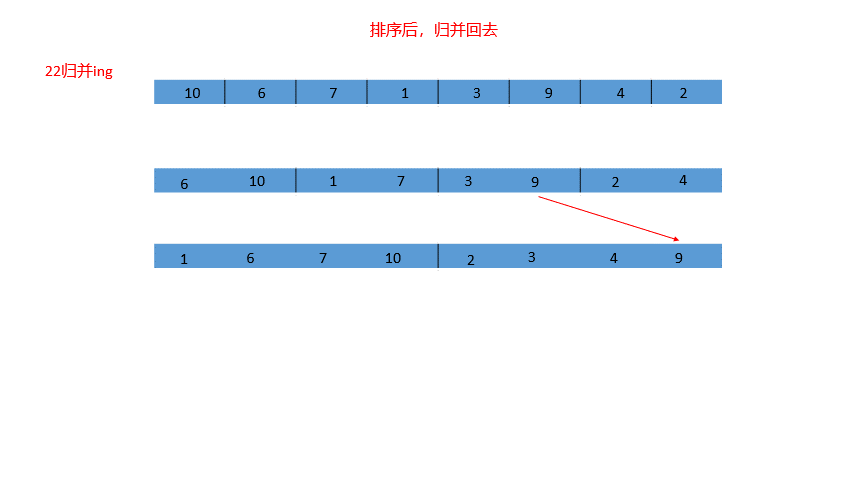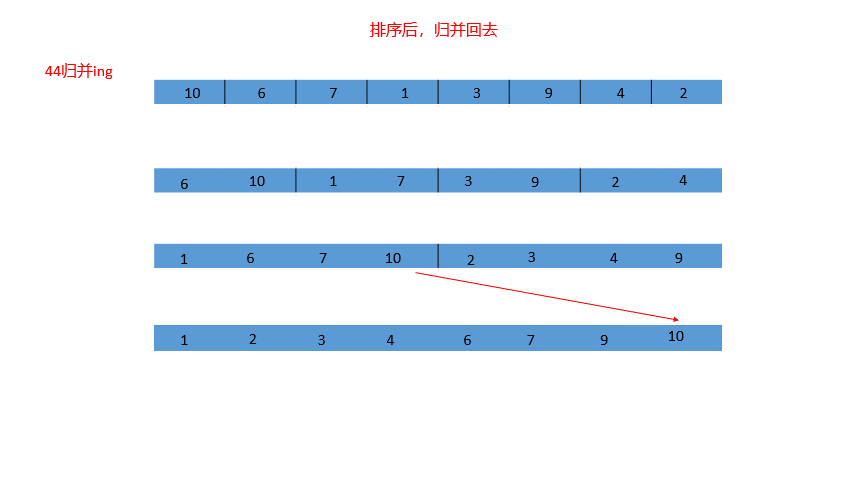机械转码日记【6】《数据结构》常见排序算法及对比【下篇】
目录
前言
1.归并排序
1.1递归实现归并排序
1.2非递归实现归并排序
2.计数排序
3.排序算法分析对比
3.1每种算法的最大时间复杂度和最小时间复杂度
3.1.1冒泡排序的最大时间复杂度和最小时间复杂度
3.1.2直接插入排序的最大时间复杂度和最小时间复杂度
3.1.3希尔排序的最大时间复杂度和最小时间复杂度
3.1.4直接选择排序的最大时间复杂度和最小时间复杂度
3.1.5堆排序的最大时间复杂度和最小时间复杂度
3.1.6快速排序的最大时间复杂度和最小时间复杂度
3.1.7归并排序的最大时间复杂度和最小时间复杂度
3.1.8计数排序的时间复杂度
3.2算法的稳定性
前言
上篇我们了解了:冒泡排序,直接插入排序,希尔排序,直接选择排序,堆排序和快速排序。那么这篇博客我们接着讲下归并排序,计数排序以及这些排序的对比分析。
1.归并排序
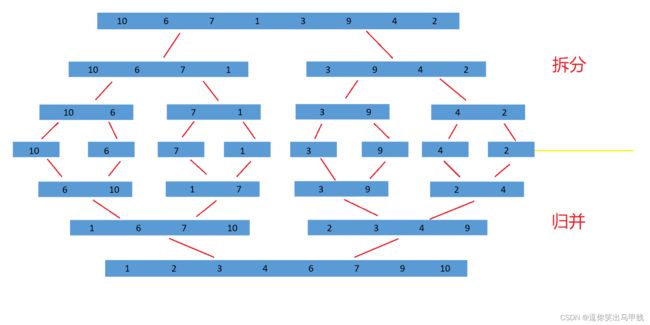
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即:先使每个子序列有序,再使父序列有序。 归并排序核心步骤如图所示:
1.1递归实现归并排序
代码实现如下:
// 归并排序递归实现
void _MergeSort(int* a, int left, int right, int*tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//[left,mid] [mid+1,right]
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);
//归并
//[left,mid] [mid+1,right]
int left1 = left, right1 = mid;
int left2 = mid + 1, right2 = right;
int index = left1;
//比较两区间元素的大小,然后写入tmp数组中对应的位置
while (left1 <= right1 && left2 <= right2)
{
if (a[left1] < a[left2])
{
tmp[index++] = a[left1];
left1++;
}
else
{
tmp[index++] = a[left2];
left2++;
}
}
//判断谁没比较完,谁没比较完就把剩下的元素写入tmp
while (left1 <= right1)
{
tmp[index++] = a[left1];
left1++;
}
while (left2 <= right2)
{
tmp[index++] = a[left2];
left2++;
}
//把tmp的元素写入a中
memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
//定义一个tmp数组存放排好序的数据
int* tmp = (int*)malloc(n * sizeof(int));
assert(tmp);
_MergeSort(a, 0, n - 1, tmp);
//防止内存泄漏,要free哦
free(tmp);
tmp = NULL;
}
这里要注意我们划分左右区间, 一定要划分成[left mid]和[mid+1,right],不可以划分成[left,mid-1]和[mid,right],因为这种分割方式会出现死循环,例如区间[1,2]就被划分成[1,0]和[1,2]了,这样反复出现[1,2]就造成死循环了。
1.2非递归实现归并排序
上一篇博客我们介绍了快速排序的非递归实现,那么归并排序我们可以用非递归来实现吗?当然可以!我们可以通过一个逐渐变大的gap变量来实现先排序小区间,再排序大区间,如图,我们控制gap = 1,2,4,8...,直到我们的gap大于我们的数组元素个数n就结束!怎么样?是不是非常方便?但是非递归实现归并排序并没有这么简单,控制边界是一件很难的事!(在这里我先卖一个关子,看看如果我们照下图的原理写代码会出现什么情况)
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
//定义一个tmp数组存放排好序的数据
int* tmp = (int*)malloc(n * sizeof(int));
assert(tmp);
int gap = 1;
while (gap < n)
{
//间距gap为1组,两两归并
for (int i = 0; i < n; i += gap * 2)
{
int left1 = i;
int right1 = i + gap - 1;
int left2 = i + gap;
int right2 = i + gap * 2 - 1;
int index = i;
//比较两区间元素的大小,然后写入tmp数组中对应的位置
while (left1 <= right1 && left2 <= right2)
{
if (a[left1] < a[left2])
{
tmp[index++] = a[left1];
left1++;
}
else
{
tmp[index++] = a[left2];
left2++;
}
}
//判断谁没比较完,谁没比较完就把剩下的元素写入tmp
while (left1 <= right1)
{
tmp[index++] = a[left1];
left1++;
}
while (left2 <= right2)
{
tmp[index++] = a[left2];
left2++;
}
}
//把tmp的元素写入a中
memcpy(a, tmp , n * sizeof(int));
gap = 2 * gap;
}
//防止内存泄漏,要free哦
free(tmp);
tmp = NULL;
}以上程序只能排序数组元素个数为4的倍数的一组数据,如果我们把数组的数据个数改成6,会发生什么呢?
果然出错了吧!原因在哪呢?我们可以看看访问数组时是否发生了越界,如何调试呢?我们可以打印出每次我们归并时访问数组的下标判断是否越界:
printf("归并:[%d,%d][%d,%d]\n", left1, right1, left2, right2);可见,在这有六个元素的数组里,我们居然访问了[6,7]和[4,7]这两个区间,这两个区间都越界了,所以这是导致我们程序出错的原因!那么我们就要控制我们的下标,不让他们越界,如何控制呢?数组越界有以下三种情况:
- 左区间的右边界越界,直接使得右边界为数组右边界
- 右区间的左边界越界,说明整个右区间都越界,就把右区间定义成一个不存在的区间
- 右区间右边界越界,直接使得右边界为数组右边界
代码实现如下:
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
//定义一个tmp数组存放排好序的数据
int* tmp = (int*)malloc(n * sizeof(int));
assert(tmp);
int gap = 1;
while (gap < n)
{
//间距gap为1组,两两归并
for (int i = 0; i < n; i += gap * 2)
{
int left1 = i;
int right1 = i + gap - 1;
int left2 = i + gap;
int right2 = i + gap * 2 - 1;
int index = i;
//防止下标越界
//三种情况
if (right1 >= n)//左区间的右边界越界,直接使得右边界为数组右边界
{
right1 = n - 1;
}
if (left2 >= n)//右区间的左边界越界,说明整个右区间都越界,就把右区间定义成一个不存在的区间
{
left2 = n;
right2 = n - 1;
}
if (right2 >= n)//右区间右边界越界,直接使得右边界为数组右边界
{
right2 = n - 1;
}
printf("归并:[%d,%d][%d,%d]\n", left1, right1, left2, right2);
//比较两区间元素的大小,然后写入tmp数组中对应的位置
while (left1 <= right1 && left2 <= right2)
{
if (a[left1] < a[left2])
{
tmp[index++] = a[left1];
left1++;
}
else
{
tmp[index++] = a[left2];
left2++;
}
}
//判断谁没比较完,谁没比较完就把剩下的元素写入tmp
while (left1 <= right1)
{
tmp[index++] = a[left1];
left1++;
}
while (left2 <= right2)
{
tmp[index++] = a[left2];
left2++;
}
}
//把tmp的元素写入a中
memcpy(a, tmp , n * sizeof(int));
gap = 2 * gap;
}2.计数排序
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 其思想为:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
原理图如下:
代码实现如下:
// 计数排序
void CountSort(int* a, int n)
{
int min = a[0];
int max = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;//算出应该创建多大的数组
int* tmp = (int*)malloc(range*sizeof(int));
assert(tmp);
memset(tmp, 0, range * sizeof(int));//给tmp数组所有元素置为0
//开始计数
for (int i = 0; i < n; i++)
{
tmp[a[i] - min]++;
}
//往回写
int j = 0;
for (int i = 0; i < range; i++)
{
while (tmp[i])
{
a[j] = i + min;//写入A数组
j++;//A数组的下标移动到下一个
tmp[i]--;//对应的数的个数减一
}
}
free(tmp);
tmp = NULL;
}
3.排序算法分析对比
3.1每种算法的最大时间复杂度和最小时间复杂度
3.1.1冒泡排序的最大时间复杂度和最小时间复杂度
当数据有序时,冒泡排序的时间复杂度为O(N),当数据为降序,而排序又要求排升序时,冒泡排序的时间复杂度为O(N^2)
3.1.2直接插入排序的最大时间复杂度和最小时间复杂度
由于直接插入排序要比较每个数,所以直接插入排序的最大时间复杂度和最小时间复杂度都为O(N^2)
3.1.3希尔排序的最大时间复杂度和最小时间复杂度
当数据为降序,而排序又要求排升序时,希尔排序的时间复杂度达到最大,为O(N^2),而希尔排序的最小时间复杂度比较难以确定,在这里引用严蔚敏老师的《数据结构(C语言版)》中所提到的一段话:
3.1.4直接选择排序的最大时间复杂度和最小时间复杂度
直接选择排序由于是与数组中所有数都比较一遍选出最大最小,所以它的大时间复杂度和最小时间复杂度都为O(N^2).
3.1.5堆排序的最大时间复杂度和最小时间复杂度
堆排序由于需要向下调整法建堆,这需要O(N)的时间复杂度,而利用堆删除思想去实现排序需要O(logN),尽管随着元素的不断删除,堆的高度越来越⼩,但是总的⽽⾔,删除堆所有元素的时间复杂度为O(NlogN)。故堆排序的时间复杂度为O(NlogN)
3.1.6快速排序的最大时间复杂度和最小时间复杂度
快速排序的最好情况是每次选key时都选到中位数,则这时的时间复杂度为O(NlogN),最坏情况是每次选key都选到最大或者最小的那个书,这时的时间复杂度为O(N^2)。
3.1.7归并排序的最大时间复杂度和最小时间复杂度
归并排序相当于二叉树的后序遍历,可以理解为一个有logN层的二叉树中,每一层都进行N次比较,因此时间复杂度为O(N*logN)。
3.1.8计数排序的时间复杂度
由前文分析可知,计数排序的时间复杂度为O(N+range),因此计数排序的时间复杂度为O(MAX(N,range)),可见它的时间复杂度是很优秀的,但是计数排序却有着O(range)的空间复杂度,因此计数排序是一种以空间换时间的算法,它比较适用于那种数据范围集中时的排序。
3.2算法的稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
以下是排序的稳定性总结:
| 排序方法 |
时间复杂度 |
空间复杂度 |
稳定性 |
|
| 最好情况 |
最坏情况 |
|||
| 冒泡排序 |
O(N) |
O(N^2) |
O(1) |
稳定 |
| 直接选择排序 |
O(N^2) |
O(N^2) |
O(1) |
不稳定 |
| 直接插入排序 |
O(N^2) |
O(N^2) |
O(1) |
稳定 |
| 希尔排序 |
O(N^1.3) |
O(N^2) |
O(1) |
不稳定 |
| 堆排序 |
O(N*logN) |
O(N*logN) |
O(1) |
不稳定 |
| 归并排序 |
O(N*logN) |
O(N*logN) |
O(n) |
稳定 |
| 快速排序 |
O(N*logN) |
O(N^2) |
O(1) |
不稳定 |
| 计数排序 |
O(MAX(N,range)) |
O(MAX(N,range)) |
O(N) |
稳定 |