广度优先遍历和深度优先遍历
广度优先遍历和深度优先遍历
- 广度优先遍历
-
- 图解
- 代码
- 深度优先遍历
-
- 图解
- 代码
广度优先遍历
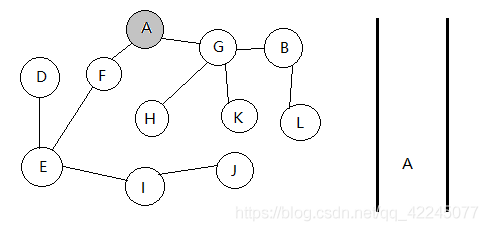
广度优先遍历是图的一种遍历方式, 它的思想就是遍历这个点相邻的所有的点, 再对这些点进行广度优先遍历. 如下图所示
图解
首先我们从A点开始遍历, 然后遍历所有和A相邻的点F和点G:
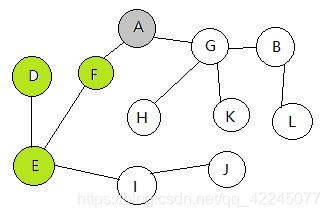
然后对F和点G进行遍历进行遍历, 得到点E, H, K和B:
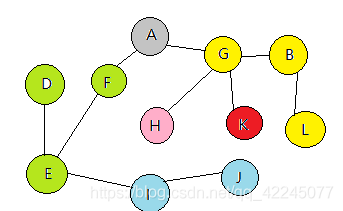
然后再继续, 知道所有的点都遍历完成:
代码
首先, 我们先定义图Graph类:
/**
* 无向图
*/
public class Graph {
/**
* 顶点的数目
*/
private final int V;
/**
* 边的数目
*/
private int E;
/**
* 邻接表
*/
private Map<Integer, Set<Integer>> adj;
public Graph(int V) {
this.V = V;
this.E = 0;
for (int i = 0; i < V; i++) {
adj.put(i, new HashSet<>());
}
}
public int getV() {
return this.V;
}
public int getE() {
return this.E;
}
/**
* 添加边
*
* @param v
* @param w
*/
public void addEdge(int v, int w) {
adj.get(v).add(w);
adj.get(w).add(v);
this.E++;
}
public Iterable<Integer> adj(int v) {
return this.adj.get(v);
}
}
接着编写BFS代码, 这里我们用一个数组marked来标记点是否被访问过, 这样我们就不需要再一次对这个点进行访问了. 同时, 我们用一个队列来保存我们遍历的节点, 每次我们都从队列中取出节点然后访问, 将新遍历的节点加入到队列中, 当队列中不在有节点是BFS就结束了:
以上图片的队列都是上进下出
/**
* 广度优先遍历
*/
public class BreadthFirstPaths {
/**
* 该顶点是否调用了bfs()
*/
private boolean[] marked;
/**
* 从起点到一个顶点的已知路径上的最后一个顶点
*/
private int[] edgeTo;
/**
* 起点
*/
private int s;
public BreadthFirstPaths(Graph g, int s) {
this.marked = new boolean[g.getV()];
this.edgeTo = new int[g.getV()];
this.s = s;
bfs(g, s);
}
private void bfs(Graph g, int s) {
List<Integer> list = new LinkedList<>();
marked[s] = true;
list.add(s);
while (!list.isEmpty()) {
int v = list.get(0);
list.remove(0);
for (int w : g.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
marked[w] = true;
list.add(w);
}
}
}
}
/**
* 判断s和v是否相连接
*
* @param w
* @return
*/
public boolean hasPathTo(int w) {
return marked[w];
}
/**
* 获取起点s到顶点v的路径
*
* @param v
* @return
*/
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) {
return null;
}
List<Integer> path = new ArrayList<>();
for (int i = v; i != s; i = edgeTo[i]) {
path.add(i);
}
path.add(s);
return path;
}
}
深度优先遍历
深度优先遍历和广度优先不同, 它的思想是每一次值找一个点, 一条路走到底, 然后在返回去遍历第二个点, 这类似于我们走迷宫一直走下去, 知道走到绝路再退回上一个路口走吓一跳道
图解
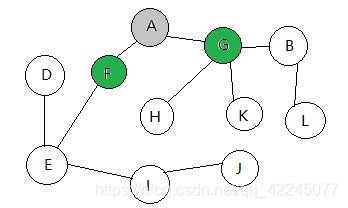
我们同样以点A作为起点, 首先我们选择一条路走到底:
走到绝路了, 退回到点E, 换一条路走:
然后再继续回退, 知道所有的点都遍历完:
代码
我们沿用刚刚定义的Graph类. 我们不难发现, DFS很容易用递归来实现:
**
* 深度优先遍历
*/
public class DepthFirstSearch {
/**
* 该顶点是否调用了dfs()
*/
private boolean[] marked;
/**
* 从起点到一个顶点的已知路径上的最后一个顶点
*/
private int[] edgeTo;
/**
* 起点
*/
private int s;
/**
* 与起点相连接的顶点数
*/
private int count;
/**
* 找出图g中所有和定点s相连的顶点
*
* @param g
* @param s
*/
public DepthFirstSearch(Graph g, int s) {
this.marked = new boolean[g.getV()];
this.edgeTo = new int[g.getV()];
this.s = s;
this.count = 0;
dfs(g, s);
}
private void dfs(Graph g, int v) {
marked[v] = true;
for (int w : g.adj(v)) {
if (!marked[w]) {
this.edgeTo[w] = v;
dfs(g, w);
}
}
}
/**
* 判断s和v是否相连接
*
* @param w
* @return
*/
public boolean hasPathTo(int w) {
return marked[w];
}
/**
* 返回和s相连接的顶点数目
*
* @return
*/
public int getCount() {
return count;
}
/**
* 获取起点s到顶点v的路径
*
* @param v
* @return
*/
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) {
return null;
}
List<Integer> path = new ArrayList<>();
for (int i = v; i != s; i = edgeTo[i]) {
path.add(i);
}
path.add(s);
return path;
}
}
当然, 我们同样的可以用栈来实现DFS, 将访问的节点入栈, 访问完就出栈, 这样也可以做到DFS:
private void dfsByStack(Graph g, int v) {
marked[v] = true;
Stack<Integer> stack = new Stack<>();
stack.push(v);
while (!stack.empty()) {
int u = stack.peek();
int w = u;
for (int i : g.adj(v)) {
if (!marked[i]) {
w = i;
break;
}
}
if (w != u) {
this.edgeTo[w] = v;
stack.push(w);
} else {
stack.pop();
}
}
}