贪心算法和拟阵

贪心算法和拟阵

动态规划能够很好的帮助我们解决很多的最优解问题，但是对于许多的最优解问题，使用动态规划进行求解会显得问题过于复杂，造成复杂度过高。贪心算法和动态规划一样是用于求解最优解问题的方法，它期望通过所做的局部最优解选择来产生一个全局最优解。

活动选择问题

有一系列相互竞争的活动，他们都需要占用同一资源，这意味着在任意时刻都不能够出现两个活动在同时进行，那么如何进行调度，能够在一段时间内进行的活动数目最大呢？

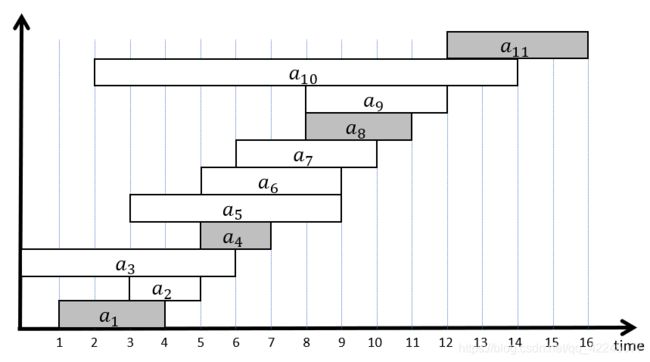
在这里，我们定义活动集合为$A=a_1,a_2,...,a_n$，他们的开始时间和结束时间定义为$s_i$和$f_i$，那么活动不冲突就是他们的活动区间$[s_i,f_i)$和$[s_j,f_j)$不重合。我们先按照活动结束时间进行排序：

i	1	2	3	4	5	6	7	8	9	10	11
$s_i$	1	3	0	5	3	5	6	8	8	2	12
$f_i$	4	5	6	7	8	9	10	11	12	13	14

我们先用动态规划的方式来求解。我们将按照结束时间单调递增的相互不冲突的活动集合定义为$S_{ij}$，其中第一个活动的开始时间不早于$f_{i-1}$，最后一个活动的结束时间不晚于$s_{j+1}$，也就是说$S_{ij}$中的每一个活动的开始时间都大于前一个活动的结束时间，对于一个活动集合$A_{ij}$，我们都可以求出其中相互兼容的活动集合$S_{ij}$。

在$A_{ij}$中，我们可以发现，对于某个活动$a_k$，存在$A_{ij}=A_{ik}\cup a_k\cup A_{kj}$，同样的，对于$A_{ij}$中相互兼容的活动$S_{ij}$，也存在$S_{ij}=S_{ik}\cup a_k\cup S_{kj}$，那么，我们就可以根据集合中每个$a_k$，将$A_{ij}$拆分成两个子集合，再分别求出子集合的最大值进行合并，比较每个不同的$a_k$拆分的结果，并取最大值即可。在这里定义$A_{ij}$中最大的相互兼容的活动集合的个数为$c_{ij}$,可以得到递归式：
$$c_{ij}=\{\begin{array}{ll}0,& A_{ij}为空\\ {\max }_{i<k<j}(c_{ijk+c_{kj}+1})& A_{ij}不为空\end{array}$$

我们再用贪心算法来解一下这个问题。在这里，我们进行一系列的选择，每一次都选择能够和之前的选择相兼容的，并且结束时间最早的活动，我们认为这样能够给接下来的选择更大的空，最后得到一个最优解为$a_1,a_4,a_8,a_{1}1$，其伪代码如下：

$S=\varphi$

将A中的活动按照结束时间从小到大排列

for x in S

if x的开始时间大于S最后一个元素的结束时间

$S=S\cup \{x\}$

return S

为什么可以进行这样的选择呢？我们定义$a_m$为$A_{ij}$中结束时间最早的活动，那么$a_m$将会在$A_{ij}$的某一个最大兼容活动子集中被使用，证明如下：

设$S_{ij}$为$A_{ij}$的一个最大兼容活动子集，$a_k$为$S_{ij}$的第一个活动，若$a_k\ne a_m$，那么我们构造子集$S_{ij}^{\prime }=(S_{ij}-\{a_k\}\cup \{a_m\})$。其中，我们很容易得出$f_m<=d_k$，所以$a_m$和$S_{ij}$中除了$a_k$以外的其他活动都是相互兼容的，即$s_{ij}^{\prime }$也是$A_{ij}$的一个最大兼容活动子集，即$a_m$在$A_{ij}$的的某一个最大兼容活动子集中被使用。

在活动选择问题中，我们既可以用动态规划解，也可以用贪心策略解，但是我们也很容易比较得出这两种方法中贪心的复杂度更小。

贪心策略和动态规划的比较

贪心和动态规划都利用的最优子结构的性质，但是动态规划是自底向上的方法，其对每一个问题都是先对子问题求解再做选择，从而得到最优解；而贪心算法则不同，他是自顶向下的方法，对于每一个问题，他都是先做出选择，在对子问题求最优解。

0-1背包问题：有$n$个物品，对于第$i$个物品，它的价格为$v_i$，重量为$w_i$，每个物品都是不可分割的完整物品，而有一个背包可以容纳总重为$W$，问背包能够装下的最大价格为多少。

部分背包问题：再0-1背包中，每一个物品都可以拿取部分，而不是只能整个整个的拿。

这两个背包问题我们都可以使用动态规划来求解，而对于部分背包问题，我们也可以使用贪心策略来求解：优先选择性价比$v_i/w_i$的物品。而对于0-1背包问题却不能使用贪心策略来求解，因为按照贪心策略做出选择后会再背包下留下无法利用的空间而在成浪费，所以应对某个物品放进去和不放进去的结果进行比较。

拟阵

对于很多的贪心问题，都可以使用拟阵来解决。

拟阵为一个序对$M=(S,l)$，其满足以下条件：

1. $S$为一个又穷的非空集合。
2. $l$为$S$的一个非空子集族，成为$S$的独立子集，其具有遗传性：若存在$B\in l$且$A\subseteq B$, 则$A\in l$。
3. 拟阵具有交换性：如果$A\in l,b\in l$，且$|A|<|B|$，则存在$x\in B-A$，使得$A\cup \{x\}\in l$。

在这里，我们用有向图来举例子：图$G=(V,E)$存在拟阵$M_G=(S_G,l_G)$，其中，$S_G=E$，即为G的边集，$l_G$为$E$中使得其构成森林的子集形成的子集族。

我们可以很快得出，因为森林的子集依然是森林，所以其具有遗传性。对于交换性，其证明如下：

我们设两个森林$G_A$和$G_B$，且$|G_A|<|G_B|$，所以可以得出$G_A$中的树多于$G_B$中的树，那么就存在$G_B$中的某棵树的某一条边，它两个顶点属于$G_A$中的两棵不同的树，即将两棵$G_A$中的树连接成了一棵树（而没有形成环），从而可以证明其交换性质。自此，可以得出每一个无向图都存在对应的拟阵。

拟阵的最大独立子集

我们成拟阵$M=(S,l)$中，对于独立子集$A\in l$，存在$A$之外的元素$x$使得$A\cup \{x\}\in l$，则成$x$为$A$的一个扩张。

对于独立子集$A\in l$,若其不存在任何扩张，则称其为最大独立子集。一个拟阵的最大独立子集的大小都是相同的。

加权拟阵

我们将拟阵的元素$x$加上权值$w(x)$，将独立子集的权值定义为它包含的所有元素的权值之和，即$w(A)={\sum }_{x\in A}w(x)$。这样，我们就可以很容易的使用贪心策略来求拟阵的最大独立子集，其伪代码如下：

$A=\varphi$

将S中的元素按照权值从大到小排列

for x in S

if $A\cup \{x\}\in l$

$A=A\cup \{x\}$

return A

而对于其他各种贪心问题，我们都可以将其转化为求拟阵的最大独立子集，下面以求带权无向连通图的最小生成树为例：

设无向连通图的各个边的权值为$w(e)$，将其转换为拟阵之后，拟阵的元素与图的边一一对应。我们设拟阵的元素的权值为$w^{\prime }(e)=w_0(e)-w(e)$，其中$w_0(e)$大于图所有边的权值。这样，拟阵权值最大的元素就对应着图权值最小的边，这样求得拟阵的最大独立子集就与图的最小生成树相对应了。