C++ OpenCV4.5 图像边缘检测Sobel、Laplance和Canny(十二)
系列文章目录
C++ OpenCV4.5环境搭建(一)
C++ OpenCV4.5常用API查询手册(二)
C++ OpenCV4.5 图像处理(三)
C++ OpenCV4.5 绘制形状与文字(四)
C++ OpenCV4.5 图像模糊(五)
C++ OpenCV4.5 项目实战一(六)
C++ OpenCV4.5 形态学操作(七)
C++ OpenCV4.5 调整图像亮度的几种方法(八)
C++ OpenCV4.5 图像金字塔和图像阈值(九)
C++ OpenCV4.5 图像的部分处理操作(十)
C++ OpenCV4.5 卷积运算和卷积边缘处理(十一)
文章目录
- 系列文章目录
- 前言
- 一、Sobel算子
-
- 1.卷积应用-图像边缘提取
- 2.Sobel算子
- 3.示例代码
- 二、Laplance算子
-
- 1.相关概念
- 2.处理步骤
- 3.相关API
- 4.示例代码
- 三、Canny边缘检测
-
- 1.算法介绍
-
-
- 2.1 处理步骤
- 2.2 非最大信号抑制
- 2.3 高低阈值输出二值图像
-
- 3.相关API
- 4.示例代码
前言
该篇主要讲述 Sobel 算子、Laplance 算子和 Canny 算法
一、Sobel算子
1.卷积应用-图像边缘提取
1. 边缘是像素值发生跃迁的地方,是图像的显著特征之一,在图像特征提取、对象检测、模式识别等方面都有重要的作用;
2. 如何捕捉/提取边缘 – 对图像求它的一阶导数 delta = f(x) – f(x-1),delta越大,说明像素在 X 方向变化越大,边缘信号越强;
2.Sobel算子
函数Sobel声明如下:
cv::Sobel (
- InputArray Src, // 输入图像
- OutputArray dst, // 输出图像,大小与输入图像一致
- int depth, // 输出图像深度
- int dx, // X方向,几阶导数
- int dy, // Y方向,几阶导数
- int ksize, // Sobel算子kernel大小,必须是1、3、5、7…
- double scale = 1, // 计算的导数值的可选比例因子,也就是缩放;默认1,不进行缩放
- double delta = 0, // 可选增量值,最终计算结果加上该值,默认0
- int borderType = BORDER_DEFAULT // 边缘处理
)
对应的微积分函数如下,符号 ∂ 为偏导数
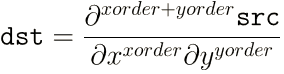
Sobel算子将高斯平滑和微分相结合,使得结果或多或少具有抗噪声能力。大多数情况下,调用函数时使用(xorder=1,yorder=0,ksize=3)或(xorder=0,yorder=1,ksize=3)计算第一个 X 或 Y 方向图像导数,分别对应下图的水平梯度和垂直梯度;
最终梯度有“平方和开根号”和“绝对值求和”两种方案,方案一效果会好一点,但计算速度相对较慢;方案二则刚好相反

输入输出深度见下表,-1是自动计算深度,为了防止像素计算超过255溢出,被截取后损失精度,输出深度至少为输入深度的两倍
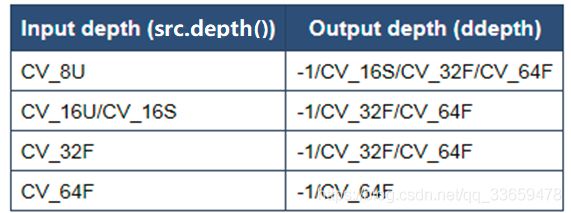
求取导数的近似值,kernel=3 时不是很准确,OpenCV使用改进版本Scharr函数,通过增加数值来扩大差异,算子如下:
cv::Scharr (
- InputArray Src, // 输入图像
- OutputArray dst, // 输出图像,大小与输入图像一致
- int depth, // 输出图像深度
- int dx, // X方向,几阶导数
- int dy, // Y方向,几阶导数
- double scale = 1, // 计算的导数值的可选比例因子,也就是缩放;默认1,不进行缩放
- double delta = 0, // 可选增量值,最终计算结果加上该值,默认0
- int borderType = BORDER_DEFAULT // 边缘处理
)
Scharr(src, dst, ddepth, dx, dy, scale, delta, borderType);
等价于
Sobel(src, dst, ddepth, dx, dy, FILTER_SCHARR, scale, delta, borderType);
3.示例代码
代码如下(示例):
#include (iRow, iCol) = saturate_cast(sqrt(pow(iX, 2) + pow(iY, 2)));
}
}
imshow("最终效果", xyGradMat);
waitKey(0);
return 0;
}
二、Laplance算子
1.相关概念
在二阶导数的时候,最大变化处的值为零,即边缘是零值。通过二阶导数计算,依据此理论我们可以计算图像二阶导数,提取边缘。
2.处理步骤
- 高斯模糊 – 降噪 GaussianBlur()
- 转换为灰度图像 cvtColor()
- 拉普拉斯 – 二阶导数计算 Laplacian()
- 取绝对值 convertScaleAbs()
- 显示图像 imshow()
3.相关API
函数 Laplacian 声明如下:
Laplacian(
- InputArray src, // 输入图像
- OutputArray dst, // 输出图像
- int depth, // 输出图像深度 CV_16S
- int kisze, // Sobel算子kernel大小,必须是1、3、5、7…
- double scale = 1, // 计算的导数值的可选比例因子,也就是缩放;默认1,不进行缩放
- double delta =0.0, // 可选增量值,最终计算结果加上该值,默认0
- int borderType = 4 // 边缘处理
)
4.示例代码
代码如下(示例):
#include 三、Canny边缘检测
Canny是一个很好的边缘检测算法,常用于图像检测处理,于1986年提出
1.算法介绍
2.1 处理步骤
- 高斯模糊 – 降噪 GaussianBlur()
- 灰度转换 – cvtColor()
- 计算梯度 – Sobel/Scharr()
- 非最大信号抑制
- 高低阈值输出二值图像 - Canny()
2.2 非最大信号抑制
本质是搜索局部极大值,抑制非极大值元素 ,算法原理我查了很多资料,看了很多博客,某博主大大的 这篇博客 写的很详细,自己也看的似懂非懂,就不献丑了
2.3 高低阈值输出二值图像
- 假设 T1、T2 为阈值,凡是大于 T2 的都保留,凡是小于T1都丢弃;T1~T2 之间,凡是大于 T1 且与边缘(大于 T2)相连接的,都保留;最终得到一个输出二值图像。
- 推荐的高低阈值比值为 T2:T1 = 3:1 / 2:1,其中T2为高阈值,T1为低阈值
3.相关API
函数 Canny 声明如下:
Canny(
- InputArray src, // 8-bit的输入图像
- OutputArray edges, // 输出边缘图像,一般都是二值图像,背景是黑色
- double threshold1, // 低阈值,常取高阈值的1/2或者1/3
- double threshold2, // 高阈值
- int aptertureSize, // Soble算子的size,通常3x3,取值3
- bool L2gradient // true表示是 L2 归一化,否则 L1 归一化,默认为 false
)
4.示例代码
代码如下(示例):
#include