【COMP202 LEC2 search tree】
LEC2
Binary Search :
If the data structure is array, it is easy to find an element. And the time complexity is O(logn). But it is expensive to update the list and maintain items in a sorted order.
If the data structure is list, it is easy to find an element. And the time complexity is O(logn). But it is difficult to add / delete an element without the knowing where to insert / delete it.
So we find a new data structure : binary search tree 二叉搜索树
Rooted tree :
>> A rooted tree, T, is a set of nodes which store elements in a parent-child relationship.
>> T has a special node, r, called the root of T.
>> Each node of T (excluding the root node r) has a parent node.
>> Two nodes that are children of the same parent are called siblings
>> A node is a leaf (external) if it has no children and internal otherwise
>> A tree is ordered if there is a linear ordering defifined for the children of each internal node (i.e. an internal node has a distinguished first child, second child, etc)
>> A binary tree is proper if each internal node has exactly two children
>> Traversal of trees 树的遍历
AVL trees :
>> Height-Balance Property: for every internal node, v, of T, the heights of the children of v can differ by at most 1.
>> An AVL tree is a tree that has the Height-Balance Property.
??????
从height of an AVL tree storing n items is O(log n) 可以推出 :
Consequence 1: A search in an AVL tree can be performed in time O(log n).
Consequence 2: Insertions and removals in AVL need more careful implementations (using rotations to maintain the height-balance property).
Insertion in AVL tree
An insertion in an AVL tree begins as an insertion in a general BST, i.e., attaching a new external node (leaf) to the tree.
>> This action may result in a tree that violates the height-balance property because the heights of some nodes increase by 1.
A bottom-up mechanism (based on rotations) is applied to rebalance the unbalanced subtrees.
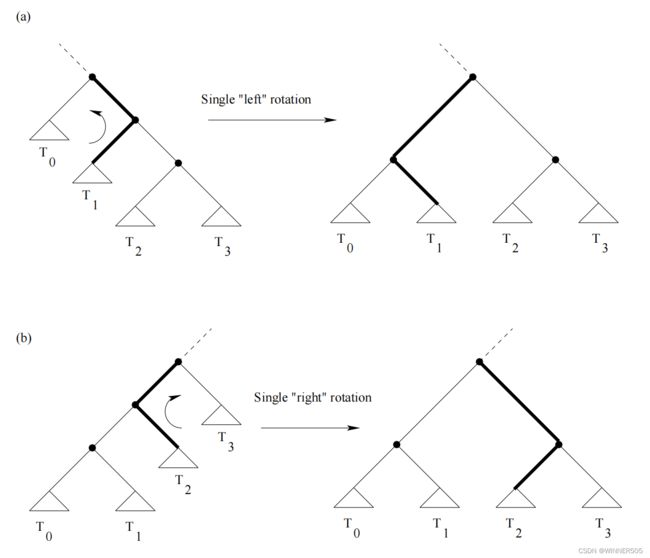
Single rotations (zig) in AVL trees
Double rotations (zig-zag) in AVL trees
Deletion in AVL trees
>> A deletion in an AVL tree begins as a removal in a general BST.
>> Action may violate the height-balance property.
>> Bottom-up mechanism (based on rotations) is applied to rebalance the tree.
(2, 4) trees
Every node in a (2, 4) tree has at least 2 and at most 4 children.
Each internal node v in a (2, 4) tree contains, 1, 2 or 3 keys defifining the range of keys stored in its subtrees.
>> Search for a key k in a (2, 4) tree T is done via tracing the path in T starting at the root in a top-down manner.
>> An insertion of k into a (2, 4) tree T begins with a search for an internal node on the lowest level that could accommodate k without violating the range.
>> This action may overflow the node-size of a node v acquiring the new key k.
>> Bottom-up mechanism (based on split-operation) is applied to fix overflflows.