中缀表达式转前缀、后缀表达式
如果有实现四则混合运算这种需求,经常会遇到如何将中缀表达式转换为前缀或者后缀表达式的问题,在用代码实现转换时,一种常见的转换方式就是使用栈结构。
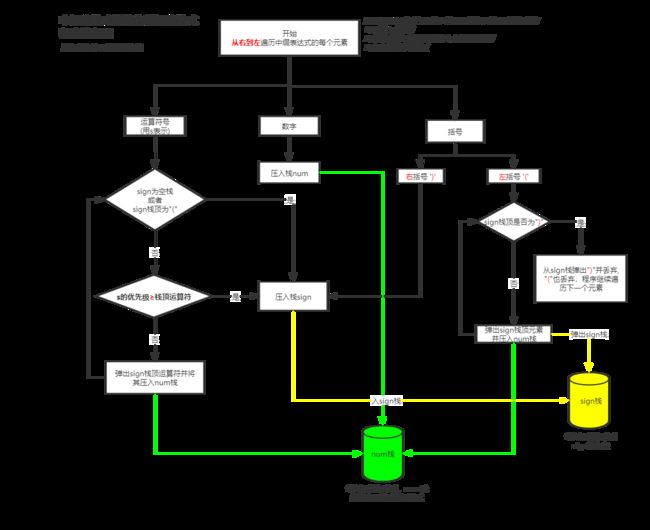
我特意整理了一个程序流程图,按照流程图写出程序就会简单很多,黑线部分就是程序的流程走向
中缀转前缀和中缀转后缀整体思路是一致的,只需要注意三个地方的区别即可
1.中缀转前缀是从右往左遍历表达式,中缀转后缀是从左往右遍历表达式;
2.运算符入栈时,对优先级的比较有所差异(中转前是≥ ;中转后是>),具体看下面的流程图红色加粗部分
3.由于遍历顺序不同,对左右括号的处理也是相反的
区分前缀和后缀的遍历顺序,以及运算符入栈的优先级比较有所区别就行。
前提条件:
创建两个栈,一个用于存储运算符("+"、"-"、"*"、"/"、"("、")"),命名为sign,一个用于存储操作数,命名为num。
转换完成后取出结果:
中缀转前缀:依次从栈顶遍历取出num栈的元素,即是前缀表达式
中缀转后缀:倒叙从栈底遍历取出num栈的元素,即是后缀表达式
中缀转前缀流程图如下
走到最后,将如果sign中还有元素,就将其依次出栈然后入栈num,若没有元素就不管sign了
最后num栈依次出栈的就是所求前缀表达式
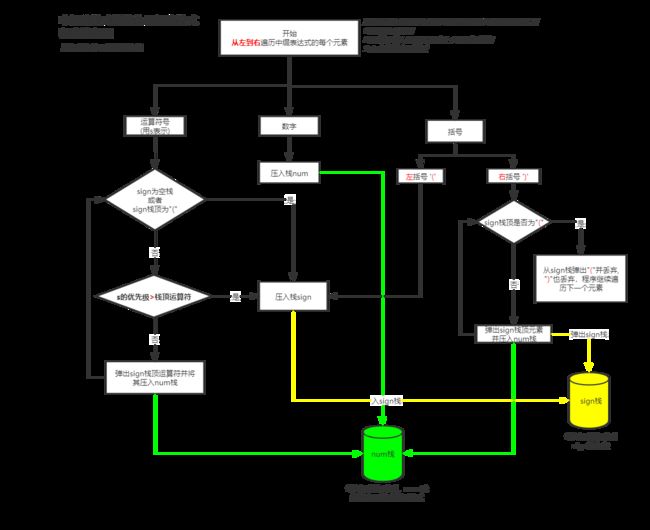
中缀转后缀流程图如下
走到最后,将如果sign中还有元素,就将其依次出栈然后入栈num,若没有元素就不管sign了
最后num栈逆序出栈的就是所求前缀表达式
具体代码实现如下,我只是通过流程图实现了代码,还没有对其做优化
计算器类Calculator
import java.util.*;
/**
*利用前缀、后缀表达式实现计算器计算个位数的四则混合运算
*/
public class Calculator {
public static final String PRE = "^[-+]?(([0-9]+)([.]([0-9]+))?|([.]([0-9]+))?)$";//数字校验正则表达式
/**
* 传入表达式,计算并返回结果
* 返回的float类型只提供 -2^31 ~ 2^31-1范围内的运算
* @param expre 传入的表达式
* @param calcWay 计算方式:前缀或者后缀
* @return 计算结果
*/
public String calculation(String expre,String calcWay){
char[] exp ;
Stack calcStack = new Stack();
float re = 0;
if (calcWay.equals("Prefix") || calcWay == "Prefix") {
exp = convertToPrefix(expre);
float a,b;
//逆序遍历,遇到数字入栈,遇到符号取出栈顶两个元素计算并将结果再次入栈
for (int i = exp.length-1; i >=0; i--) {
if(exp[i] == '+' || exp[i] == '-' || exp[i] == '*' || exp[i] == '/'){
//取出栈顶两个元素并计算
a = calcStack.pop();
b = calcStack.pop();
switch (exp[i]){
//注意运算时,大数在前,小数在后,不然减法和乘法会计算错误
case '+':calcStack.push(a+b);break;
case '-':calcStack.push(a-b);break;
case '*':calcStack.push(a*b);break;
case '/':calcStack.push(a/b);break;
}
}else{
calcStack.push((float) exp[i] - '0');
}
}
re = calcStack.peek();//栈中最后一个元素即为计算结果
System.out.println("前缀表达式为"+String.valueOf(exp));
}
else if(calcWay.equals("Suffix") || calcWay == "Suffix"){
exp = convertToSuffix(expre);
System.out.println("后缀表达式为"+String.valueOf(exp));
float a,b;
for (int i = 0; i < exp.length; i++) {
if(exp[i] == '+' || exp[i] == '-' || exp[i] == '*' || exp[i] == '/'){
//取出栈顶两个元素并计算
a = calcStack.pop();
b = calcStack.pop();
switch (exp[i]){
//注意运算时,大数在前,小数在后,不然减法和乘法会计算错误
case '+':calcStack.push(b+a);break;
case '-':calcStack.push(b-a);break;
case '*':calcStack.push(b*a);break;
case '/':calcStack.push(b/a);break;
}
}else{
calcStack.push((float) exp[i] - '0');
}
}
re = calcStack.peek();//栈中最后一个元素即为计算结果
}
else {
throw new RuntimeException("计算方式只能为'Prefix'或者'Suffix'");
}
//计算完成后,若为正数,就去掉float后面的小数点和0
String result = (Math.round(re)-re==0) ? String.valueOf((long)re) : String.valueOf(re);
return result;
}
/**
* 转换为前缀表达式
* @param expre
* @return
*/
public char[] convertToPrefix(String expre){
char[] preFix = expre.toCharArray();
Stack sign = new Stack<>();
Stack num = new Stack<>();
for(int i = preFix.length-1;i>=0;i--){//从右到左遍历表达式
if(preFix[i] == ')'){
sign.push(preFix[i]);
}
else if(preFix[i] == '('){
if(sign.peek() == ')'){
sign.pop();//弹出'(' 丢弃
}else{
//遍历sign栈,并将其中的元素弹出压栈到num栈,直到找到左括号就弹出并结束
while (sign.size()>0){
if(sign.peek() == ')') {
sign.pop();//直到栈顶元素为 ')'结束并丢弃括号
break;
}
num.push(sign.pop());
}
}
}
else if(preFix[i] == '+' || preFix[i] == '-' || preFix[i] == '*' || preFix[i] == '/'){
if(sign.empty() || sign.peek() == ')'){//为空或顶部元素为')'就直接压栈
sign.push(preFix[i]);
}
else{
if(isHighOrEqualThan(preFix[i],sign.peek())){//当前的运算符比栈顶元素优先级高
sign.push(preFix[i]);
}
else{
while (true){
//遍历sign栈,将栈顶元素取出并压入num栈
// 直到遇到')'或者sign栈空 又或者找到一个元素优先级比当前元素高
if(sign.empty() || sign.peek() == ')' || isHighOrEqualThan(preFix[i],sign.peek())) {
sign.push(preFix[i]);
break;
}
num.push(sign.pop());
}
}
}
}
else if(String.valueOf(preFix[i]).matches(PRE)){ //正则验证是否为是数字,直接入栈
num.push(preFix[i]);
}
else{
throw new RuntimeException(preFix[i]+"不是数字和运算符,请检查输入的算式是否正确");
}
}
//遍历完成后,将sign剩余的所有符号依次出栈push到num栈中
while (sign.size()>0) num.push(sign.pop());
char[] result = new char[num.size()];
//逆序获取num栈并保存到结果数组
for(int forntIndex = 0;num.size()>0;forntIndex++){
result[forntIndex] = num.pop();
}
return result;
}
/**
* 转换为后缀表达式
* 转换流程图参考:https://blog.csdn.net/c_o_d_e_/article/details/108774118
* @param expre
* @return
*/
public char[] convertToSuffix(String expre){
char[] suffix = expre.toCharArray();
Stack sign = new Stack<>();
Stack num = new Stack<>();
for(int i = 0;i0){
if(sign.peek() == '(') {
sign.pop();//直到栈顶元素为 '('结束并丢弃括号
break;
}
num.push(sign.pop());
}
}
}
else if(suffix[i] == '+' || suffix[i] == '-' || suffix[i] == '*' || suffix[i] == '/'){
if(sign.empty() || sign.peek() == '('){//为空或顶部元素为'('就直接压栈
sign.push(suffix[i]);
}
else{
if(isHighThan(suffix[i],sign.peek())){//当前的运算符比栈顶元素优先级高
sign.push(suffix[i]);
}
else{
while (true){
//遍历sign栈,将栈顶元素取出并压入num栈
// 直到遇到'('或者sign栈空 又或者找到一个元素优先级比当前元素高
if(sign.empty() || sign.peek() == '(' || isHighThan(suffix[i],sign.peek())) {
sign.push(suffix[i]);
break;
}
num.push(sign.pop());
}
}
}
}
else if(String.valueOf(suffix[i]).matches(PRE)){ //正则验证是否为是数字,直接入栈
num.push(suffix[i]);
}
else{
throw new RuntimeException(suffix[i]+"不是数字和运算符,请检查输入的算式是否正确");
}
}
//遍历完成后,将sign剩余的所有符号依次出栈push到num栈中
while (sign.size()>0) num.push(sign.pop());
char[] result = new char[num.size()];
//逆序获取num栈并保存到结果数组
for(int lastIndex = result.length-1;num.size()>0;lastIndex--){
result[lastIndex] = num.pop();
}
return result;
}
/**
* 比较两个运算符的优先级signOb是否高于compareOb
* @param signOb 要比较的符号
* @param compareOb 比较的对象
* @return true表示sign优先级高于compareOb
*/
public static boolean isHighThan(char signOb,char compareOb){
if((signOb == '+' || signOb == '-') && (compareOb == '*' || compareOb == '/'))//低于
return false;
else if((signOb == '+' || signOb == '-') && (compareOb == '+' || compareOb == '-')) //相同
return false;
else if((signOb == '*' || signOb == '/') && (compareOb == '*' || compareOb == '/')) //相同
return false;
else if((signOb == '*' || signOb == '/') && (compareOb == '+' || compareOb == '-')) //高于
return true;
else
throw new RuntimeException("该符号不是加减乘除:sign:"+signOb+",compareOb:"+compareOb);
}
/**
* 比较两个运算符的优先级signOb是否高于或等于compareOb
* @param signOb 要比较的符号
* @param compareOb 比较的对象
* @return true表示sign优先级高于compareOb
*/
public static boolean isHighOrEqualThan(char signOb,char compareOb){
if((signOb == '+' || signOb == '-') && (compareOb == '*' || compareOb == '/'))//低于
return false;
else if((signOb == '+' || signOb == '-') && (compareOb == '+' || compareOb == '-')) //相同
return true;
else if((signOb == '*' || signOb == '/') && (compareOb == '*' || compareOb == '/')) //相同
return true;
else if((signOb == '*' || signOb == '/') && (compareOb == '+' || compareOb == '-')) //高于
return true;
else
throw new RuntimeException("该符号不是加减乘除:sign:"+signOb+",compareOb:"+compareOb);
}
}
测试类Main
import java.util.*;
public class Main {
public static void main(String args[]){
System.out.println("请输出四则混合运算表达式(仅限于个位数):");
Calculator calc = new Calculator();
Scanner scn = new Scanner(System.in);
while(scn.hasNext()){
String expres = scn.nextLine();
System.out.println("请输入计算方式,Prefix(前缀)或Suffix(后缀):");
String fix = scn.nextLine();
System.out.println(calc.calculation(expres,fix));
}
}
}测试结果如下图
![]()