因果推理概念再细化和梳理
0x01. 背景
前期看了一篇因果推理的综述,经阅读后对其进行了简单的整理,也有一些方法和细节不太熟悉,遂再次进行梳理,将理解不通透的概念重新整理。
0x02. 回顾基本概念
- unit: 因果推理中的原子研究对象,可以是实物,也可以是概念,可以是一个或者多个。在一些框架下,不同时刻的同一对象被认为是不同的units。
- treatment: 施加给unit的操作。也叫做干预、介入等。
- variables: unit自带的一些属性,比如患者的年龄,性别,病史,血压等。在treatment过程中不受影响的variable叫做pre-treatment variables,比如患者的性别在多数情况下是不变的;对应的,受到影响的variable叫做post-treatment variables。
- Confounder: 会影响treatment选择和结果的一些变量。比如同一剂量的药剂在不同年龄的人群的结果可能不一样,或者说不同年龄的药剂选择会不同。有一些文献中也叫做协变量,covariate。
- potential outcome: 施加给对象的操作所能产生的所有可能产生的结果。包含observed outcome和反事实结果。
- factual outcome: 施加给对象的操作最终观测到的结果,记做Y。
- propensity score: 倾向分数。 e ( x ) = P r ( W i = 1 ∣ X i = x ) e(x) = Pr(W_i = 1|X_i = x) e(x)=Pr(Wi=1∣Xi=x),反映出样本 x x x选择 t r e a t m e n t treatment treatment的可能性。
- selection bias: 选择偏差。由于 C o n f o u n d e r Confounder Confounder的存在, t r e a t m e n t treatment treatment组和 c o n t r o l control control组的分布有可能不一致,因此导致出现偏差,这也使得推理更加困难。
- pre-treatment variables : 不受干预影响的变量,也叫做背景变量,比如吃药问题的天气。
- post-treatment variables : 受干预影响的变量,比如吃药问题中的食欲。
ATE(Average Treatment Effect): A T E = E [ Y ( W = 1 ) ] − E [ T ( W = 0 ) ] ATE = E[Y(W=1)] - E[T(W=0)] ATE=E[Y(W=1)]−E[T(W=0)],所有人的平均treatment effect。
ATT(Average Treatment Effect on the Treated group): A T T = E [ Y ( W = 1 ) ∣ W = 1 ] − E [ Y ( W = 0 ) ∣ W = 0 ] ATT=E[Y(W=1)|W=1] -E[Y(W=0)|W=0] ATT=E[Y(W=1)∣W=1]−E[Y(W=0)∣W=0],受处理群体的平均处理效应。
ATC(Average Treatment Effect on the Controled group): 与ATT相似,是对照组的平均干预效果。
ITE(Individual Treatment Effect): I T E i = Y i ( W = 1 ) − Y i ( W = 0 ) ITE_i=Y_i(W=1)−Y_i(W=0) ITEi=Yi(W=1)−Yi(W=0),某个unit(个体维度)的treatment effect。
CATE(Conditional Average Treatment Effect): C A T E = E [ Y ( W = 1 ) ∣ X = x ] − E [ Y ( W = 0 ) ∣ X = x ] CATE=E[Y(W=1)∣X=x]−E[Y(W=0)∣X=x] CATE=E[Y(W=1)∣X=x]−E[Y(W=0)∣X=x],在特征 X = x X = x X=x的子人群里面treatment effect。
0x03. 辛普森悖论
之前只知道辛普森悖论是一种看起来有优势,在总评测中却拉跨的一种现象。重新理解后才知道,辛普森悖论是一个统计学中的名词,大概意思是为了探究两种变量的相关性,人们会对变量之间分组研究,然而出现一个问题是:在分组比较中都占优势的一方,在总评的时候有时反而是失势的一方。
此处引用知乎的一个例子:
| 男100人 | 女100人 | |||||
|---|---|---|---|---|---|---|
| 申请 | 录取 | 录取率 | 申请 | 录取 | 录取率 | |
| 工科 | 80 | 38 | 47.5% | 20 | 14 | 70% |
| 文科 | 20 | 2 | 10% | 80 | 16 | 20% |
| 总计 | 100 | 40 | 40% | 100 | 30 | 30% |
这里统计了两个学院男生和女生的申请人数,录取人数以及录取率,这里隐含的辛普森悖论是:无论是物理学院还是文学院,男生的个别录取率都小于女生,但是计算总计的录取率男生却远大于女生。当时录取结果出来时,人们议论这个学校是不是对女生存在性别歧视,但是当你看不同分组的录取率时,你会发现它歧视男生?到底是歧视谁呢?
为什么会出现这种情况?
辛普森悖论的本质是,或者说前提是,每层之间的成功率差别很大。:录取率数据中,无论是男生还是女生,工科学院的录取率都远高于文学院(这里可能是学校专业分配上的原因,工科学院更好考吧,没有文科那么卷);
工科学院更容易考,总结来说就是做了更容易做的事。观察数据发现,不同批次的人分配做不同难度事的人也是有差别的,这也是悖论的第二个前提。更多男生申请了工科学院(选择更容易的事去做),导致最终统计成功率时出现反转。
总结一下:如果你多去干成功率高的事,那你整体的成功率就会变大。
再次引用知乎大佬的几何解释:
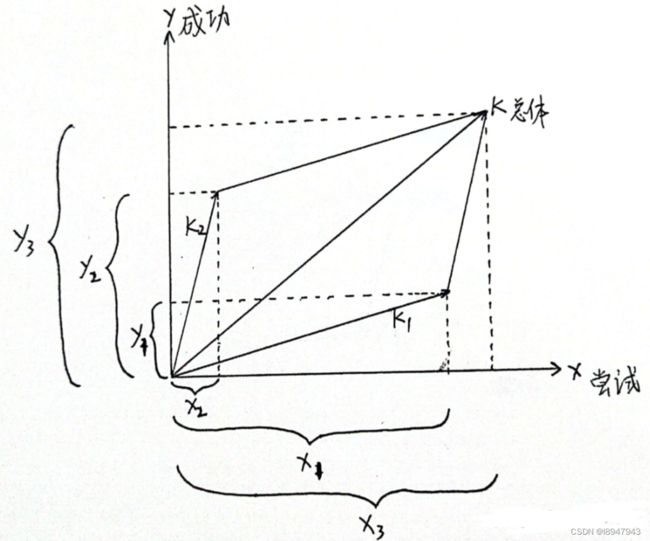
我们以横坐标表示做某件事尝试的次数,纵坐标表示成功次数,每一个事件都可以用直角坐标系中的一个点来表示,画一个指向这个坐标点的向量,向量的斜率表示的就是成功率。假设一个人做了两件事,一件事的成功率记为 k1,另一件事的成功率记为 k2;那么总体的成功率该怎么计算呢?很简单,总体成功率 = 总的成功次数 / 总的尝试次数,在几何上,根据平行四边形法则,以这两个向量作为邻边做一个平行四边形,而这个平行四边形对角线的斜率就是总体的成功率。
这样子就能解释,为什么一个人两层的成功率都不高(相对的),但是总体的成功率偏高。

A无论做第一件事还是第二件事,成功率都小于B,但是计算总的成功率却大于B。
辛普森悖论的启示:为了避免辛普森悖论的出现,需要斟酌个别分组的权重,以一定的系数去消除以分组分层差异所造成的影响。虽然数据是客观和真实的,但是不同的人却可以用同样的数据讲出不同的故事。