与时间赛跑：图算法如何加持自然灾害应急响应场景？
近日，受台风“杜苏芮”影响，华北、黄淮等地出现极端降雨过程，引发洪涝和地质灾害，造成京津冀地区的重大人员伤亡和财产损失。大家的心都被这场暴雨牢牢牵动着。
而在7月31日晚，小编的微信朋友圈开始被《京津冀暴雨紧急求助信息登记表单》《北京暴雨紧急求助信息入口》《京津冀暴雨求助信息统计汇总表》几个文档刷屏。这是由专业救援机构和志愿者组织对接，为北京、河北、天津等地区因暴雨被困人员提供的特殊紧急求助渠道。通过该文档，救援人员不仅能够快速开展救援行动，还能够更好地研判灾情和分配救援力量。文档建立后，五湖四海的朋友们都立刻开始自发转载分享。
同时在微博上，@北京日报在8月1日发起的#京津冀暴雨互助#相关话题迅速登上热搜，受到超亿人的关注，数千名志愿者加入。尽管一个人的力量十分微小，但大家都希望给京津冀地区的朋友提供力所能及的支持，共同用温暖守护风雨中的ta。
在数千条的求救信息里，小编也发现，非常多的求助信息都提到了 “如何合理施救”“救援物资有限”“通行路线受阻” 等关键词。
事实上，传统的应急管理工作因极端环境的变化会遇到更多的挑战。
一方面，自然灾害大多存在突发性，要求应急管理中心在最快速度对自然灾害进行预警、评估、应对、恢复。而传统的应急管理主要依赖领域专家知识，以人工经验进行灾害应急管理，需要耗费大量的时间和人力资源，较难达到灾害应急的高时效性要求，易造成大量的经济损失。
另一方面，自然灾害相关的多元维度数据规模骤增，现有的数据资源无法有效共享、难以进行知识发现和知识转化增值等问题日益明显。激增的数据资源和智能化应用需求之间出现矛盾，严重制约灾害应急响应能力的提升。
因此，“如何高效利用数据资源，做到实时、精准、可靠的应急管理”，“如何打破恶劣环境限制，实现救援队伍、物资、专家的合理调度”，“如何快速决策，最大程度保障人民群众财产和生命安全”等问题，成为自然灾害应急响应中心亟须解决的问题。
在此背景下，图技术凭借实时数据分析、隐藏关系发掘和情境化精准决策的优势，能够为自然灾害风险防控与应急保障保驾护航的关键力量。
本文中，笔者将聚焦灾后救援时间段，介绍图算法在救援区域总基地的选址、全局救援路径网络规划、替代路径选择等具体场景的应用，从而深度探讨图算法与自然灾害应急响应之间的关系，分析图技术在构建自然灾害应急响应实时精准决策体系中可发挥的关键作用。
场景介绍
下文中对区域性应急救援总基地选址、全局救援路径网络规划、局部最优替代救援路径规划、小型救援补给点设定四个场景中可选用的图算法进行介绍。
A. 区域性应急救援总基地选址
场景需求
应急救援基地建设是应急救援能力提升的基础。考虑到受灾地点往往是涉及到大面积区域，而救援基地是整个救援行动的心脏位置，选址需要满足快速、最小代价辐射区域中其他地点的需求。
可应用算法介绍
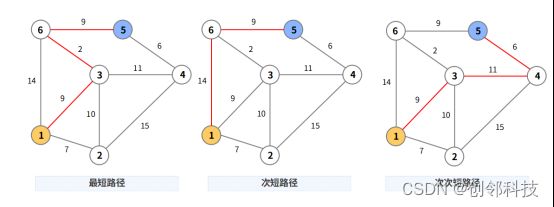
中介中心性算法（Betweenness Centrality)： 通过计算全图任意两点之间的最短路径，统计一个点在上述最短路径中出现的次数，计算出最终得分。找到触达全图中所有点代价最小的点的算法。下图为计算点1中介中心性得分的过程，最终点1的中介中心性得分为19/6。
图1 | 中介中心性算法概念图
应用场景示例
如某地受灾区域各地点之间的联通关系如下图所示：
图2 | 某地受灾区域地点与联通关系示意图
不同地点之间存在多种路径，且因为受灾程度不同，通行方式受限，部分只适用于步行。可以将步行与乘车的耗时进行标准化换算后作为边属性入图，即可形成如下图所示的各地点间不同通行方式的耗时图：
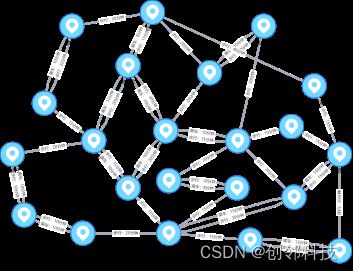
图3 | 各地区间通行方式耗时示意图
在上图中，运行带边权重的中介中心性算法即可发现触达全图中所有点代价最小的点为地点7，则可将地点7设为本次应急响应工作的总基地，特点为：全域路径最佳、支撑迅速高效。
图4 | 基地与各地联通关系示意图
B. 全局救援路径网络规划
场景需求
现实场景中，往往存在多个待救援点以及多个终点，想要有效开展救援行动需要对救援路线进行合理规划。其中，考虑到受灾地点的环境变化较大，且不同的通行方式面对不同的通行环境具有不同的效率。
因此，需要采用图算法进而实时绘制救援路线的能力。
可应用算法介绍
最小生成树（Minimum Spanning Tree）： 对于一个连通带权图，选定一个顶点作为根，系统地遍历图中的所有顶点和边，遍历时经过的顶点、边所构成的子图，称为图的生成树。生成树中边的权重之和最小的生成树称为最小生成树。
以下为计算步骤：
- 始化最小生成树为空。选择任意一个顶点作为起始点。
- 从剩余的边中选择权重最小的边，如果该边连接的两个顶点之一已经在最小生成树中，则忽略该边（避免形成环）。
- 将选择的边加入最小生成树，并将边连接的另一个顶点加入最小生成树的顶点集合中。
- 重复步骤2和步骤3，直到最小生成树包含了图中所有的顶点。
- 最小生成树生成完毕。
在每一步中，我们选择权重最小的边，并确保所选边的两个顶点中至少有一个顶点不在当前的最小生成树中。这样可以避免形成环，同时保证最小生成树的连通性。
通过这些步骤，我们可以逐步构建出一棵最小生成树，该树连接了图中所有的顶点，并且权重之和最小。
图5 | 最小生成树算法概念图
应用场景示例
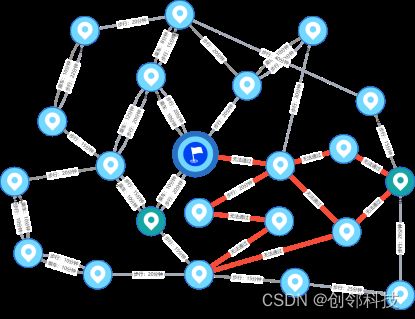
选择本次应急响应工作的总基地地点7为起始点，运行最小生成树算法，即可自适应规划以地点7为起始点的全局最优路径，路径结果如下图所示：
图6 | 总基地相关全局最优路径示意图
C. 局部最优替代救援路径规划
场景需求
在执行应急响应任务中，因时间紧急，救援队伍完成某任务后往往需要直接前往下一个任务点，而不是返回总基地进行休息补给，此时全局最优的路径规划便不一定适用。
同时应急响应地点还需要考虑环境的多变性，因为很多自然灾害会引发连锁反应和次生灾害，例如强降雨会引发山洪暴发和山体滑坡，此时部分路径的通行会受到影响。
所以对于救援队伍而言，需要具备依据具体情况智能规划局部最优路径的能力。
可应用算法介绍
K-最短路径（Yen’s Shortest Path）： 选择图中的两个节点，从起始点和终止点同时搜索，直到相遇。相遇后，在把起始点到交点和交点到终止点的路径合起来便是最短路径，可返回从起始点到终止点之间的前K条最短路径。下图为点1到点5之间最短三条路径。
图7 | K-最短路径算法概念图
应用场景示例
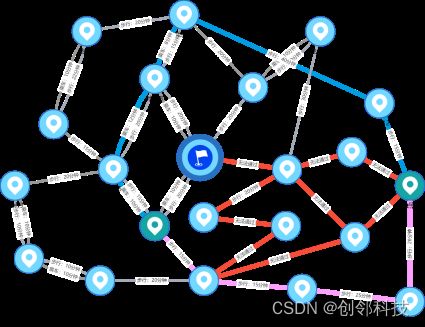
救援队伍A位于地点15，现需要前往地点19进行紧急救援，而部分路径因环境变化已不可通勤，部分道路只可通过步行通过，具体情况如下图：
图8 | 救援场景点边示意图
通过选中地点15与地点19，将标红线路的通行成本设为无穷大后，运行K-最短路径算法，即可生成多条替代路径：
图9 | 替代路径选择示意图
D. 小型救援补给点设定
场景需求
救援过程需要大量的物质，既无法每次都回总基地补给身上又不能太多，所以需要尽可能在所有人能够简单触达的地方开设小型补给点。
可应用算法介绍
最大独立集（Maximum Independent Set）： 最大独立集是指图中不相邻的节点组成的集合，其中任意两个节点之间没有边相连。（红点为最大独立集）
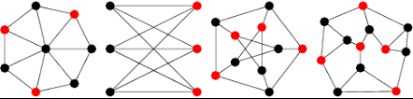
图10 | 最大独立集算法概念图
应用场景示例
基于图3构建的图运行最大独立集算法后，即可得到下图：
图11 | 最大独立集算法运行示意图
由此可见，在上图的红色地点设计小型补给点，即可让处在该地区的所有救援队通过本地补给或者简单的移动获得补给，增加救援队的安全性与资源保障。
总结
通过上图的场景介绍，我们能够了解到图算法在救援选址、路径规划等场景的应用可能，利用图关联分析、快速量化灾区的交通情况和路径长短，更实时、精准地定位救援基地、通行路径。
在实际情况中，图技术能够和大数据、云计算等前沿技术相结合，赋能城市原有的防灾减灾抗灾应急管理综合平台提升应急救援保障和后勤决策部署能力，在高度时间敏感的情况下，实现更快、最优的决策，最大程度降低损失。
感兴趣的友友们如果想要了解更多图技术在自然灾害应急响应场景的解决方案，欢迎扫描下方微信号添加创邻科技小助手，加入交流群，共同探讨应用可能。
未来，创邻科技将以自身技术优势，着力推动图技术在自然灾害防控系统中的应用，推进应急资源管理数据的分析和利用，和上下游企业积极合作，形成最大合力，最大程度保障人民群众的生命和财产安全。