ADC原理的仿真分析

1. 模数转换
模数转换充当了模拟信号向数字信号的转换站，模拟信号因为容易受到干扰，信号处理时容易受到其他条件的限制，且不易存储的特点，在实际处理经常换成数字信号。在输出时，再又转换成模拟信号，典型的应用就是D类功放。在ADC信号链中至少包括5个部分：前端传感器，信号调理，抗混叠滤波，输入防护，ADC。在模拟部分ADC是终端，在数字部分ADC是输入端，因此ADC是链接模拟和数字信号的核心模块。

2. ADC的工作原理
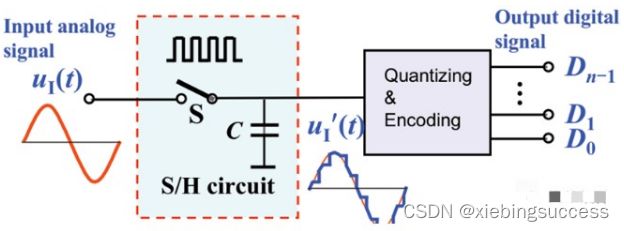
ADC完成了模拟信号向数字信号的转变，实现ADC转换的器件主要包括下面4个过程：采样——保持——量化——编码。

对应的电路如下所示：

目前市场上出现了很多类型的ADC，如果深入到ADC内部的细节看，采样和保持电路基本一样，但是在量化和编码方面却存在非常大的区别。正式这种区别 ，才产生了类似SAR，pipeline等之类不同的ADC架构。

2.1采样定理
模拟信号随时间连续变化，而数字信号是离散的，要得到转换后的数字信号第一步就是获取到模拟信号，即对模拟信号采样。因为数字信号无法做到随时间连续，所以只能间隔一定的时间对输入信号进行取样。在单位时间对模拟信号采样次数，被称为采样率，单位是Ksps。根据香浓定理，为了能将取样信号还原成输入的信号则必须满足

其中fs是取样频率，fimax是输入模拟信号的最高频率分量的频率。在实际的电路设计中，通常采样频率3~5倍的输入信号频率。在采样的过程中，通常会涉及到两个定理容易被搞混淆，一个是香浓采样定理，另外一个是奈奎斯特采样定理，通常也成为奈奎斯特——香浓取样定理。

 2.2 S/H保持电路
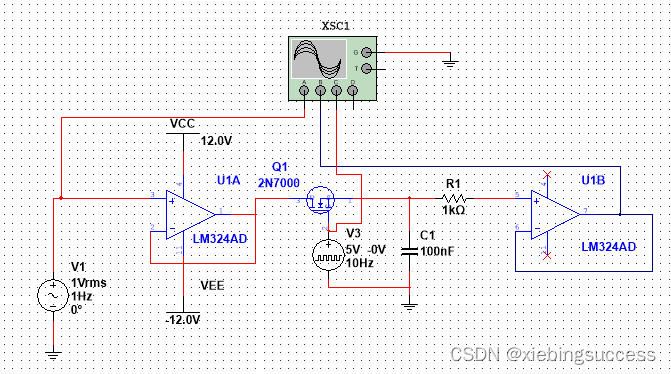
保持电路的核心就是将采样后的模拟信号保持一段时间，在这段时间内信号要保持不变，能让后级的数字电路完成量化和编码。通常采用电容作为取样后的保持器件。原理如下所示：

 图中的电容C即为保持电容。采样开关和保持电容通常作为一个整体，成为S/H电路。A1和A2是两个运放，接成跟随的形式。这两个运放在IC里面是真实存在的，A1是用来隔离前面的信号，同时利用正向输入电阻无穷大的特性。A2是用来隔离后面的信号，利用输出阻抗在20~50Ω的特性。两边都是运放，把S/H电路夹在中间，可以降低噪声。根据前面采样和保持电路的原理，可以对前两个过程进行仿真。

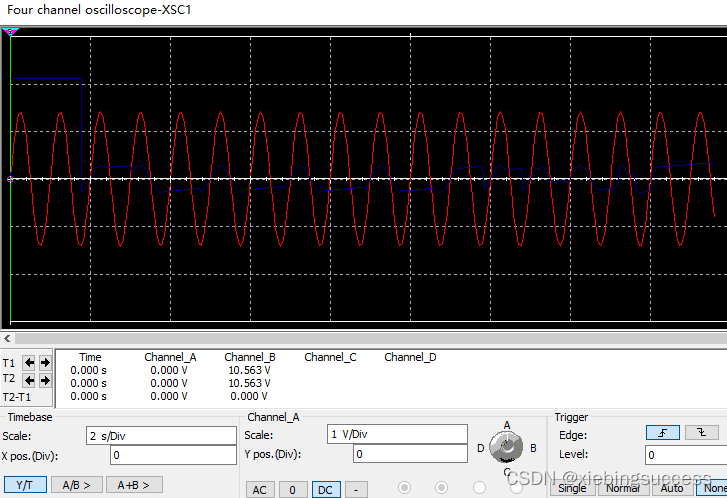
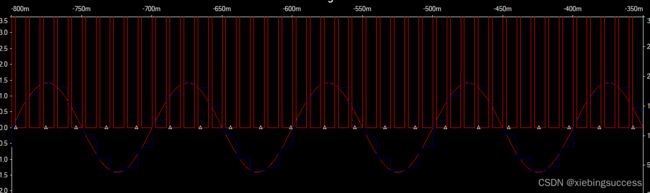
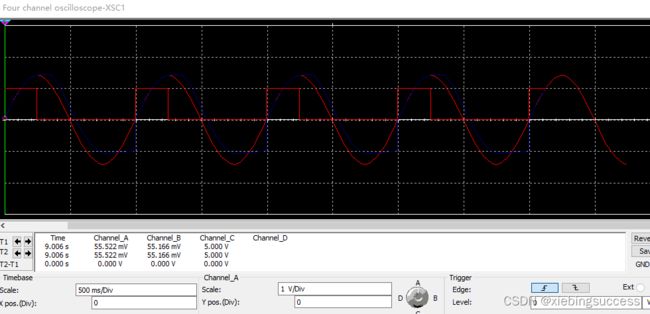
假设现在采样的速率比较低，手动就可以满足条件，从下面的波形可以看出，红色是原始波形，蓝色是采样到的信号，存在较大的失真，也就是无法正常还原采样的信号。

使用MOS管代替开关后，加入采样的驱动频率，仿真的结果可以看出，红色波形是输入信号，蓝色是采样后的信号，基本上能将输入信号进行还原。

 

 

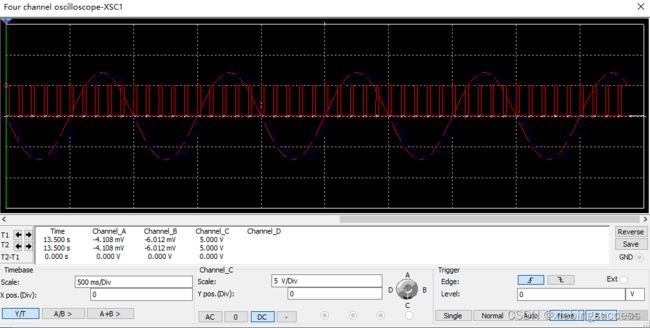
 现在来做个采样定理的测试实验，将采样频率设置为输入信号频率一样，此例为1HZ，则得到的波形图如下：

 将采样频率设置为2倍输入信号频率，此例为2HZ，则得到的波形图如下：

 可以看到至少为2倍的输入信号频率才能将取样信号还原成输入的信号则，验证了2.1的采样定理。

2.3 量化
量化是指将连续的模拟信号用有限个离散的数字信号近似化，量化后的模拟信号被划分为有限个且具有相同幅度的阶距的集合，如下图所示。

原始的模拟信号是连续无限的，用来量化的数字信号是离散有限的，那么在量化的过程中，会因为阶距的数量有限，部分模拟信号会被同一个量化后的值代替。从上图也可以看出，当离散后的数字信号为某一定值时，此时的模拟信号是在连续变化，因此，被量化的原始信号和量化后的信号之间存在差值，这种差值就是量化误差。根据量化误差的定义可知，假如我们用无穷多个离散值来量化模拟信号，则每个阶距就是一个点，那么和原始信号几乎就是一样，没有量化误差，但实际并不可能存在，所以量化误差存在的根本原因是量化时所使用的分辨率是有限的。分辩率(Resolution)和精度经常被混淆，在初中物理我们学过，分辨率是用来描述刻度划分，精度是用来描述准确度。比如我们有两把直尺，都是10cm，一把直尺上面有100个小刻度，另外一把直尺上有10个刻度，那么前者的分辨率是1mm，后者的分辨率是1cm。显然前者的分辨率要比后者高。在ADC中刻度的划分使用数字信号的位数来表示，比如理想的8位ADC分辨率就不如18位的ADC。精度表示测量值和真实值之间的误差，或者说测量值偏离真值的幅度。使用两个相同分辨率的ADC来测量同一个模拟量，测出的结果也不可能完全相同，在不考虑量化误差的前提下，ADC本身会由于器件材料和工艺制程的影响，导致测量值偏离真实值。为了描述这种精度的大小，较常使用的是绝对精度和相对精度。绝对精度：用电压分辨率(LSB)的倍数表示，如 ± 1/1LSB 、± 1LSB 等。相对精度 ：用绝对精度除以满量程值的百分数表示 。量化编码的不同导致不同ADC的类型。

2.4 编码
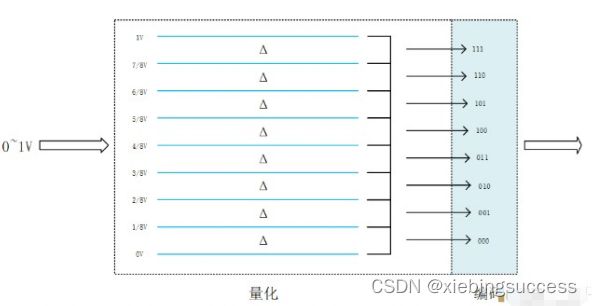
编码是ADC内部转换的最后一个过程，将量化后的结果，用二进制或者其他进制的形式表示出来，就是编码的过程。经过编码后，原始的模拟信号成为了数字信号。编码的本质是输出一串数字代码，这个代码会尽可能的接近当前采样到的模拟值。因此，使用哪种方式进行量化，将决定编码的规则。现在有一个3位的ADC，对输入0~1V的电压进行量化编码，其过程如下。3位ADC则可以将输入信号进行8等阶距的量化。

从量化的过程可以看出，当输入的电压在0~1/8V之间的任意一个模拟值时，此时输出的编码均是000，在1/8~2/8V之间的任意电压时，此时输出编码值均为001。那么这个量化过程引入最大的量化误差为1/8V，也就是量化时等阶距的值，一个1LSB。随着分辨率的增加，可以将模拟量量化为多位，因此分辨率增加，量化误差可以减少。随着数字电路的发展，ADC其实大多数人用的越来越少，并不是因为ADC不用了，而是上游的芯片公司把ADC做到了芯片里面，直接以数字信号进行输出。但是无论是分离式的信号链，还是集成在芯片内部，ADC的整体框架没有变。

ksps：kilo Samples per Second 表示每秒采样千次，是转化速率的单位。所谓的转换速率(Conversion Rate)是指完成一次从模拟到数字的AD转换所需的时间的倒数。积分型AD的转换时间是毫秒级属低速AD，逐次比较型AD是微秒级属中速AD，全并行/串并行型AD可达到纳秒级。采样时间则是另外一个概念，是指两次转换的间隔。为了保证转换的正确完成，采样速率(Sample Rate)必须小于或等于转换速率。因此有人习惯上将转换速率在数值上等同于采样速率也是可以接受的。常用单位是ksps和Msps，表示每秒采样千/百万次（kilo / Million Samples per Second）。1msps=1000ksps。

在AD转换中，有一个重要的参数，那便是转换精度。转换精度主要可以分为理论转换精度和实际转换精度。理论转换精度，我们也可以称为AD转换器的分辨率。一般我们可以按位数将AD转换器分为4位、6位、8位…等等。位数越高，分辨率也就越高。一般来说，n位的AD转换器的分辨率为2的n次方。例如：4位的AD转换器分辨率为2^4。12位的转换器为2^12。假如量程是5V，用12位的转换器采集电压时，能采集得到的最小电压值为5/2^12=1.2（mV）。这1.2mv就是该12位AD转换器的最大测量长度，也就是量程定下来了以后，12位即把这个量程分成4096等分，每一等分是：量程 / 4096。如果我们想让最大测量长度变得更小，精度更高，我们可以增加AD转换器的位数。例如使用16位的AD转换器进行采集，这样就会变为：5/2^16=0.08（mV）。