About Multiple regression

ps:this article is not very strict,just some ml and mathematic basic knowledge.My english is poor too.So If this passage make you confuse and uncomfortable.Please give me a feedback in the comment :-D

Prior to this(在此之前), we learned the concept of single feature version. There is a model consists of only one feature ,denote as X. But in some situations, such as a real estate agency,we have to considerate more elements,size,floor,age....and so on.After analyzing all there factor ,  a useful and conprehensive model will emerge.

First,we shall need to learn some notitions:

• feature: this term is set to donate one of a training example. For example, a training example contains mang features like "name,age,height,width,color..and so on"
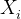•  : j-th feature
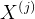• ：features of i-th training example
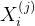• :the value of j-th feature of features of i-th training example

The description of model function also changes:

• pre： f（x）=wx+b
• new   f（x）=w1x1+w2x2+w3x3......+b

For this new version, in this linear model with two or more features,we entitle this model as 'multiple linear regression'.

Vectorization:

When we have many features,our model will become complex: f(x)=w1x1+w2x2+w3x3+w4x4+w5x5......... It not only results in too many code,but also randers a heavy time and space cost. so we can use veciorization to simplify this model.Fonnlty , we have a linear mathematical library in python.

• x=[x1,x2,x3,x4........]
• w=[w1,w2,w2,w4........]
• f(x)=wx+b

#in python library ‘NumPy’，we can use it 
w=np.array([x1,x2,x3]) 
x=np.array([w1,w2,w3]) 
b=4 
f=np,dot(x,w)+f 

#the function 'dot' implements dot product. 
# less codes,faster counting 

So,we get a useful skill. But how to iteration? Yep,we have more features than before. these features also need to iterate.In the gradient descend,just memory that simultaneously update

(repeat simyltaneously update) w1=w1-.... ...... b=b-,,,,,

Sacling(放缩)

In other hands，we can also say ‘rescale’.when one of feature has a too big or small scale or range,like this

• x1: 0 to 10
• x2: 0 to 2000
• x3: 0 to 10 x2 is overscale compared with other features.It will render a disproportative 'topograph' that lines converge to one axis in graph,like this: 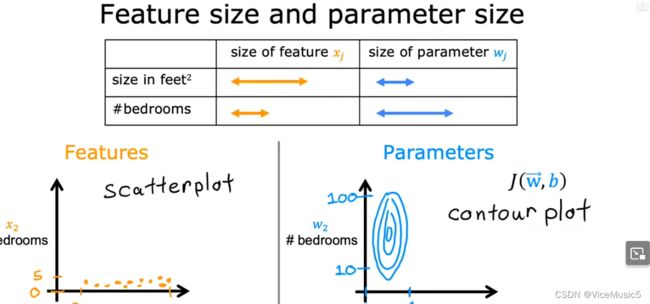 So,we can rescale this feature.there are more methods to finish this goal，and I like this :  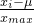    (u is average value of all same feature in different training example).
• Also there are a lot of methods，I will use them behind,

 

how to check convergence:

In the pervious blog, I use some notion which defined in other subject to discribe how to judge what time can we abort iteration. Making sure you parameters is working correctly.J should decrease after every iteration.And If J decreases by < 0.001(a communal number) in one interation , then declare converge.

how to choose learning rate Too big rate may be diperse in a gradience .

 

however , a too small is reliable than bigger though it will make it slower. Well,our method is set a enough small value as original rate.If J can converge with this rate,we try to lightly improve rate until we have a suit rate for this model. like:0.001,0,005,0,01.....progressivily imporve and guess.

plus

Feature engineer: design new features by tranforming or combincing basing on original features.

 

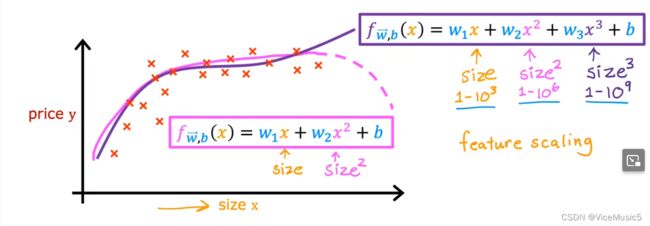
polynomial regression: no-linear,maybe multiple features.