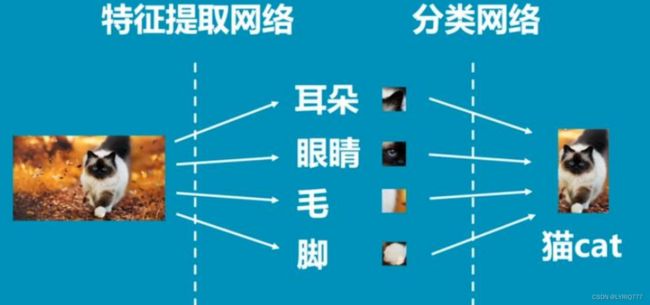
卷积神经网络

卷积神经网络

CNN就是著名的卷积神经网络，是一种前馈神经网络。

CNN不同于传统的神经网络只有线性连接，CNN包括卷积（convolution）操作、汇合（pooling）操作和非线性激活函数映射（即线性连接）等等。

经典的CNN网络有Alex-Net、VGG-Nets、Resnet等。

之前提到了卷积,什么?!卷什么,卷积!卧槽,DNA动了,积你太美!!!baby

咳咳,鸡哥别冲动,言归正传,我们现在来回顾一下:

卷积的作用

1. 特征提取：卷积可以通过滤波器提取出信号中的特征，比如边缘、纹理等。这些特征对于图像分类和识别任务非常重要。
2. 降维：卷积可以通过池化操作减小图像的尺寸，从而降低数据的维度。这对于处理大规模图像和文本数据非常有用。
3. 去噪：卷积可以通过滤波器去除信号中的噪声。这在信号处理和图像处理领域中非常常见，有助于提高数据的质量。
4. 图像增强：卷积可以通过一些滤波器对图像进行增强，比如锐化、平滑等。这有助于提高图像的视觉效果和品质。

卷积的意义

1. 模拟生物视觉：卷积操作模拟了人眼对图像进行观察、辨认的过程，因此卷积在图像处理领域应用广泛。它可以帮助我们理解人类视觉系统如何工作，并且为我们提供了一种有效的处理图像和语音的方法。
2. 提升算法性能：卷积神经网络（CNN）是目前深度学习中最重要的模型之一，其基本结构就是卷积层，卷积操作在图像识别、语音识别和自然语言处理等领域提升了算法的性能。这使得卷积成为了现代机器学习和人工智能的重要组成部分。
3. 数据压缩：卷积可以通过降维和滤波等操作减小数据的尺寸，从而实现数据的压缩。这对于处理大规模数据、实现数据存储和传输非常有用。

我们又知道,深度学习是非常强大的

那么,卷积+深度学习有没有搞头?!

 哎,容量够小,深度够深,哎~~~~~~~有东西啊

于是乎CNN(卷积神经网络就来了)

卷积网络与之前的网络结构不同之处在于，它可以直接接受多维向量，而我们以前实现的网络只能接收一维向量

怎么理解这句话?听好了,接下来我要开始装X了.

众所周知,图片分为长(H),宽(W),通道(C),几个维度了,三个了吧,是不是多维了.看下图:

CNN过程

如图:这是特斯拉Model S,0~60英里只需要3.7秒,呸!看右边!

这是卷积的过程:

CONV:卷积

RELU:relu激活函数

激活函数的作用:

关于神经网络中的激活函数的作用，通常都是这样解释：不使用激活函数的话，神经网络的每层都只是做线性变换，多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够，所以这时候就体现了激活函数的作用了，激活函数可以引入非线性因素

POOL:吃货(操!这该死的输入法),池化!!!

池化层的作用:

神经网络中的一种常用操作，主要用于降低特征图的维度、减少参数数量、提高模型的鲁棒性和泛化能力等方面

看上图,发现什么规律了没,每个色块池化之后,组合成的数字,一定是最大的那个,为啥捏?!特征啊.夜空中最亮的星, 能否听清...(我想你了,开始网抑云时刻)

1,2,3,网抑云时间结束,写完继续emo

FC:全连接（Fully Connected，FC）

得出结果,然后归一化(softmax)进行分类

其中,前三个可以根据需要自由组合,分类可以作为下一个网络的输入.

 

• 卷积操作，其实是把一张大图片分解成好多个小部分，然后依次对这些小部分进行识别。

• 通常把一张图片分解成多个3*3或5*5的”小片“，然后分别识别这些小片段，最后把识别的结果集合在一起输出给下一层网络。

• 这种做法在图象识别中很有效。因为它能对不同区域进行识别，假设识别的图片是猫脸，那么就可以把猫脸分解成耳朵，嘴巴，眼睛，胡子等多个部位去各自识别，然后再把各个部分的识别结

果综合起来作为对猫脸的识别。

卷积核

图片的采样器也可以叫做共享权值，用来在图片上采集信息。卷积核有自己的长宽，也可以定义自己的步长stride ，每跨多少步进行一次抽离信息，跨的步长越多就越容易丢失图片信息。然后

对抽取的信息进行像素的加权求和得到Feature Map 增加了采集结果的厚度。

总而言之,卷积是用来不断的提取特征，每提取一个特征就会增加一个feature map，所以采集后的图片厚度不断变厚

你可以这么理解,跨一步就是一个结果,这个结果根据步长,存在map里(Key-Value)

{
    "s1": "value1",
    "s2 ": "value2 "
}

like this

问题

这里遇到一个情况,如果卷积核一开始是固定的话,不管是高斯还是sobel,都是写死的,不准啊,总不能每跑一次程序都去修改卷积核吧,那TM不累死了?!!!

哎,动态卷积核,怎么调整呢,神经网络里有什么?

有神经.-_-!,我刀呢!!!

反向传播啊!大哥.

怎么做?训练

看我上一篇推理和训练_LYRIQ777的博客-CSDN博客(刷阅读量了属于是)

这里有很多人不理解,卷积核是怎么更新的,我一开始也没理解,然后看了一下几位大佬的博客并结合一些资料

CNN | 03卷积层的训练_训练卷积核_“逛丢一只鞋”的博客-CSDN博客

 卷积神经网络（CNN）的训练过程、权值更新_cnn网络权重怎么训练的_boringApp的博客-CSDN博客

深度学习之卷积神经网络CNN（二）训练方法_cnn网络训练_liuy9803的博客-CSDN博客

过程不想写了,写的头疼,看的也头疼,我现在对数学的认知停留在1+1=3

假设一个卷积核是3*3大小,那么对应的权重值其实就是9(3*3)个,以一层为例,那么就是w1~w9权重,多层同理

注意,这里都是针对最大池化,平均池化的话,需要把原先的池化结果进行均分

写到这边差不多了,see you next time

明天又要上班了,为了梦想奋斗(我的梦想就是不上班)