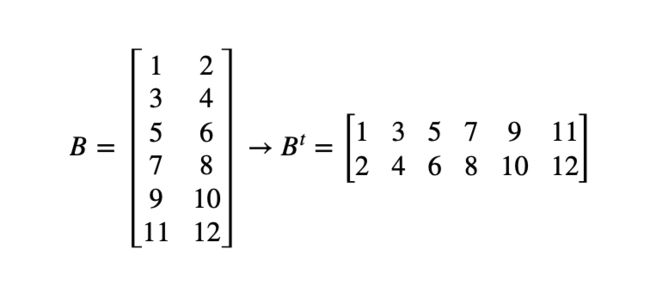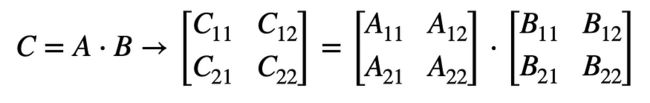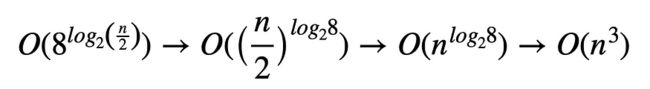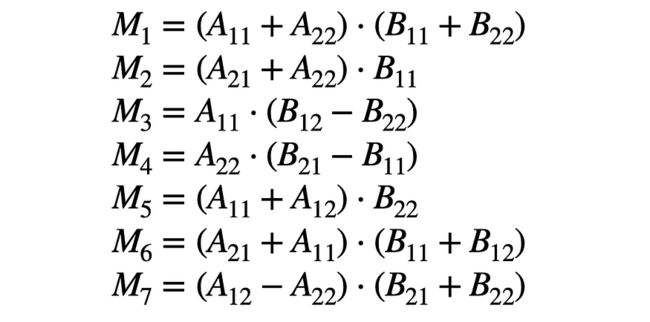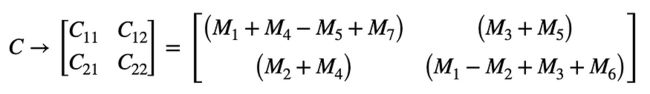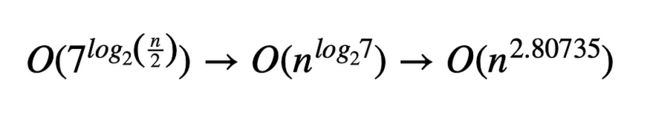优于立方复杂度的 Rust 中矩阵乘法
中途:三次矩阵乘法
一、说明
几年前,我在 C++ 年编写了 Strassen 矩阵乘法算法的实现,最近在 Rust 中重新实现了它,因为我继续学习该语言。这是学习 Rust 性能特征和优化技术的有用练习,因为尽管 Strassen 的算法复杂性优于朴素方法,但它在算法结构中的分配和递归开销中具有很高的常数因子。
- 通用算法
- 换位以获得更好的性能
- 次立方:斯特拉森算法的工作原理
- 排比
- 标杆
- 分析和性能优化
二、通用算法
一般(朴素)矩阵乘法算法是每个人在他们的第一堂线性代数课上学习的三个嵌套循环方法,大多数人会将其识别为 O(n³)
pub fn
mult_naive (a: &Matrix, b: &Matrix) -> Matrix {
if a.rows == b.cols {
let m = a.rows;
let n = a.cols;
// preallocate
let mut c: Vec = Vec::with_capacity(m * m);
for i in 0..m {
for j in 0..m {
let mut sum: f64 = 0.0;
for k in 0..n {
sum += a.at(i, k) * b.at(k, j);
}
c.push(sum);
}
}
return Matrix::with_vector(c, m, m);
} else {
panic!("Matrix sizes do not match");
}
} 这种算法很慢,不仅因为三个嵌套循环,还因为按列通过而不是按行的内部循环遍历对于 CPU 缓存命中率来说是可怕的。Bb.at(k, j)
三、换位以获得更好的性能
转置朴素方法允许 B 上的乘法迭代在行而不是列上运行,将矩阵 B 的乘法步幅重新组织为更有利于缓存的格式。从而变成A x BA x B^t
它涉及一个新的矩阵分配(无论如何,在这个实现中)和一个完整的矩阵迭代(一个 O(n²) 操作,更准确地说,这种方法是 O(n³) + O(n²))——我将进一步展示它的性能有多好。它如下所示:
fn multiply_transpose (A: Matrix, B: Matrix):
C = new Matrix(A.num_rows, B.num_cols)
// Construct transpose; requires allocation and iteration through B
B’ = B.transpose()
for i in 0 to A.num_rows:
for j in 0 to B'.num_rows:
sum = 0;
for k in 0 to A.num_cols:
// Sequential access of B'[j, k] is much faster than B[k, j]
sum += A[i, k] * B'[j, k]
C[i, j] = sum
return C 四、次立方:斯特拉森算法的工作原理
要了解 Strassen 算法的工作原理(此处为 Rust 代码),首先考虑矩阵如何用象限表示。要概念化它的外观:
在朴素算法中使用此象限模型,结果矩阵 C 的四个象限中的每一个都是两个子矩阵乘积的总和,总共产生 8 次乘法。
考虑到这八个乘法,每个乘法都在一个块矩阵上运行,其行和列跨度约为 A 和 B 大小的一半,复杂性相同:
斯特拉森算法定义了由这些象限组成的七个中间块矩阵:
仅通过 7 次乘法而不是 8 次乘法计算。这些乘法可以是递归斯特拉森乘法,并可用于组成最终矩阵:
由此产生的亚立方复杂度:
五、排比
中间矩阵 M1 的计算 ...M7 是一个令人尴尬的并行问题,因此也很容易检测算法的并发变体(一旦你开始理解 Rust 关于闭包的规则)。
/**
* Execute a recursive strassen multiplication of the given vectors,
* from a thread contained within the provided thread pool.
*/
fn
_par_run_strassen (a: Vec, b: Vec,
m: usize, pool: &ThreadPool)
-> Arc>> {
let m1: Arc>> = Arc::new(Mutex::new(None));
let m1_clone = Arc::clone(&m1);
pool.execute(move|| {
// Recurse with non-parallel algorithm once we're
// in a working thread
let result = mult_strassen(
&mut Matrix::with_vector(a, m, m),
&mut Matrix::with_vector(b, m, m)
);
*m1_clone.lock().unwrap() = Some(result);
});
return m1;
} 六、标杆
我编写了一些快速的基准测试代码,该代码在不断增加的矩阵维度范围内运行四种算法中的每一种进行几次试验,并报告每种算法的平均时间。
~/code/strassen ~>> ./strassen --lower 75 --upper 100 --factor 50 --trials 2
running 50 groups of 2 trials with bounds between [75->3750, 100->5000]
x y nxn naive transpose strassen par_strassen
75 100 7500 0.00ms 0.00ms 1.00ms 0.00ms
150 200 30000 6.50ms 4.00ms 4.00ms 1.00ms
225 300 67500 12.50ms 9.00ms 8.50ms 2.50ms
300 400 120000 26.50ms 22.00ms 18.00ms 5.50ms
[...]
3600 4800 17280000 131445.00ms 53683.50ms 21210.50ms 5660.00ms
3675 4900 18007500 141419.00ms 58530.00ms 28291.50ms 6811.00ms
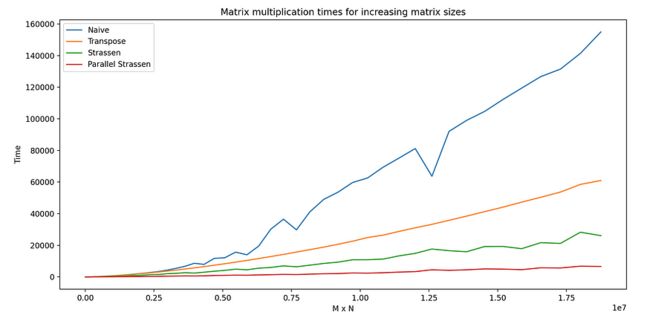
3750 5000 18750000 154941.00ms 60990.00ms 26132.00ms 6613.00ms 然后,我通过以下方式可视化结果:pyplot
此图显示了矩阵从 7.5k 元素 () 到大约 19 万 () 的乘法时间。你可以看到朴素算法在计算上变得不切实际的速度有多快,在高端需要两分半钟。N x M = 75 x 100N x M = 3750 x 5000
相比之下,Strassen 算法的扩展更平滑,并行算法计算两个 19M 个元素的矩阵的结果,而朴素算法只处理 3.6M 个元素所花费的时间。
对我来说最有趣的是算法的性能。如前所述,缓存性能的改进(以牺牲完整矩阵副本为代价)在这些结果中得到了清楚地证明 - 即使使用与该方法渐近等效的算法也是如此。transposenaive
七、分析和性能优化
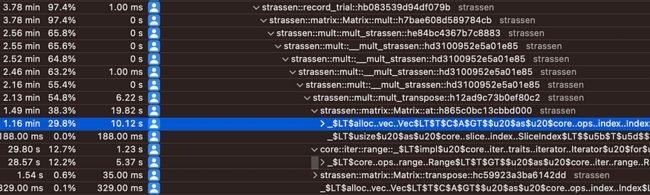
这个文档是理解 Rust 性能基础知识的绝佳资源。在 Mac OS 上启动并运行仪器进行分析是微不足道的,这要归功于货运仪器的 Rust 指南。这是调查分配行为、CPU 热点和其他事情的绝佳工具。
在此过程中发生了一些变化:
- Strassen 代码通过分而治之策略递归调用自己,但是一旦矩阵达到足够小的大小,其高常数因子使其比一般矩阵算法慢。我发现这个点是大约 64 的行宽或列宽;通过提高吞吐量提高几个因素来增加此阈值
2 - 斯特拉森算法要求矩阵填充到最接近的指数 2;减少这种情况以懒惰地确保矩阵只有偶数行和列 通过减少昂贵的大分配,将吞吐量提高了大约两倍
- 将小矩阵回退算法从 更改为 导致大约 20% 的改进
naivetranspose - 添加和添加到 Cargo.toml 发布构建标志大约提高了 5%。有趣的是,性能持续恶化
codegen-units = 1lto = "thin"lto = “true” - 一丝不苟地删除所有可能的副本大约提高了~10%
Vec - 提供一些提示并删除随机访问查找中的向量边界检查,又提高了大约 20%
#[inline]
/**
* Returns the element at (i, j). Unsafe.
*/
#[inline]
pub fn at (&self, i: usize, j: usize) -> f64 {
unsafe {
return *self.elements.get_unchecked(i * self.cols + j);
}
}参考资料: