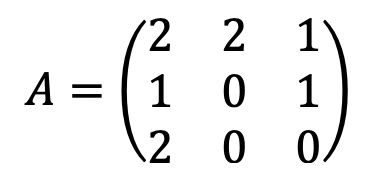回到未来：使用马尔可夫转移矩阵分析时间序列数据

一、说明

        在本文中，我们将研究使用马尔可夫转移矩阵重构时间序列数据如何产生有趣的描述性见解以及用于预测、回溯和收敛分析的优雅方法。在时间上来回走动——就像科幻经典《回到未来》中 Doc 改装的 DeLorean 时间机器一样。

        注意：以下各节中的所有方程和图表图像均由本文作者创建。

二、基本构建基块

        让 E 定义构成时间序列数据的 k 个唯一事件的集合。例如，时间序列可能由以下三个基本且独特的事件组成，这些事件表示在跨离散时间步长绘制数据时观察到的路径轨迹类型：向下、横盘和向上。让 S 定义一个长度为 n 的序列（表示离散时间步长），由 E 中定义的事件组成，表示部分或全部数据。例如，序列 [向上、向下、向上、横盘、向上] 表示数据的五个时间步长。

        现在可以定义一个维度为 k² 的马尔可夫转移矩阵 M，使得每个元素 M（i， j） 描述在给定时间序列中从时间步长 t 中的事件 E（i） 过渡到时间步长 t+1 中的事件 E（j） 的概率。换句话说，M（i， j） 表示在连续时间步长内在两个事件之间转换的条件概率。在图论意义上，事件 E（i） 和 E（j） 可以被认为是由有向边 E（i） → E（j） 连接的节点，如果时间序列数据中的 E（i） 后跟 E（j）; 则马尔可夫转移矩阵 M 本质上表示图中节点所描述的事件的邻接矩阵（或共生矩阵）的规范化版本。

接下来，让我们看看我们可以用这些基本构建块做什么。

三、过渡矩阵的实际应用：一个简单的例子

        假设我们有以下涵盖 11 个连续时间步长的原始时间序列数据：[1， 2， -2， -1， 0， 0， 2， 2， 1， 2， 3]。 使用上述路径轨迹的简化视图，我们可以将数据转换为以下 10 个事件的序列，这些事件描述了相邻时间步之间的转换：[向上、向下、向上、向上、向上、向上、向上、向上、 平坦，向上，持平，向下，向上，向上]。

现在，我们可以构造以下邻接矩阵，用于捕获事件序列中的重合模式：

        元素 A（i， j） 表示在我们的事件序列中，事件 i 在某个时间步 t 处后跟事件 j 在时间步长 t+1 的次数;i 和 j 分别是行索引和列索引。请注意，行按从上到下的顺序表示事件，列表示从左到右的顺序相同。例如，A 的左上角元素表示在给定事件序列中，一个 up 事件后跟另一个 up 事件两次。A 的右中元素表示，在事件序列中，一个横盘事件后跟一个下降事件。等等。

        我们可以按行或按列规范化矩阵 A 以生成过渡矩阵。如果我们要使用基于行的规范化，那么元素 M（i， j） 将描述在时间步长 t+1 中看到事件 E（j） 的概率，给定时间步长 t 中的事件 E（i）。因此，每行中的概率总和应为 1。在我们的示例中，行规范化矩阵如下所示：

        同样，如果我们要使用基于列的归一化，那么元素 M（i， j） 将描述在给定时间步长 t 中的事件 E（j） 的情况下，在时间步长 t-1 中具有事件 E（i） 的概率。现在，每列中的概率总和应为 1。在我们的示例中，列规范化矩阵如下所示：

        请注意，行规范化的条件概率（名义上是向前移动）可能与列规范化的条件概率（向后看时间）不同。

四、Python 代码中的示例

        为了尝试这些概念，这里有一些基本的 Python 代码，用于捕获上面示例中发生的情况。

        确保先安装了 Pandas 软件包：

pip install pandas==0.25.2

然后运行以下代码：

import pandas as pd

# Define helper functions
def get_transition_tuples(ls):
    ''' Converts a time series into a list of transition tuples
    '''
    return [(ls[i-1], ls[i]) for i in range(1, len(ls))]

def get_transition_event(tup):
    ''' Converts a tuple into a discrete transition event
    '''
    transition_event = 'flat'
    if tup[0] < tup[1]:
        transition_event = 'up'
    if tup[0] > tup[1]:
        transition_event = 'down'
    return transition_event

# Generate raw time series data
ls_raw_time_series = [1, 2, -2, -1, 0, 0, 2, 2, 1, 2, 3]

# Derive single-step state transition tuples
ls_transitions = get_transition_tuples(ls_raw_time_series)

# Convert raw time series data into discrete events
ls_events = [get_transition_event(tup) for tup in ls_transitions]
ls_event_transitions = get_transition_tuples(ls_events)

# Create an index (list) of unique event types
ls_index = ['up', 'flat', 'down']

# Initialize Markov transition matrix with zeros
df = pd.DataFrame(0, index=ls_index, columns=ls_index)

# Derive transition matrix (or co-occurrence matrix)
for i, j in ls_event_transitions:
    df[j][i] += 1  # Update j-th column and i-th row

''' Derive row-normalized transition matrix:
- Elements are normalized by row sum (fill NAs/NaNs with 0s)
- df.sum(axis=1) sums up each row, df.div(..., axis=0) then divides each column element
'''
df_rnorm = df.div(df.sum(axis=1), axis=0).fillna(0.00)

''' Derive column-normalized transition matrix:
- Elements are normalized by column sum (fill NAs/NaNs with 0s)
- df.sum(axis=0) sums up each col, df.div(..., axis=1) then divides each row element
'''
df_cnorm = df.div(df.sum(axis=0), axis=1).fillna(0.00)

这应该产生以下转移矩阵：

>>> df  # Transition matrix with raw event co-occurrences
      up    flat  down
up    2     2     1
flat  1     0     1
down  2     0     0
>>> df_rnorm  # Row-normalized transition matrix
      up    flat  down
up    0.4   0.4   0.2
flat  0.5   0.0   0.5
down  1.0   0.0   0.0
>>> df_cnorm  # Column-normalized transition matrix
      up    flat  down
up    0.4   1.0   0.5
flat  0.2   0.0   0.5
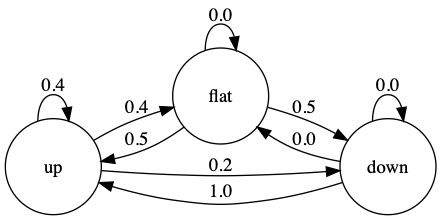
down  0.4   0.0   0.0

        可视化转移矩阵的一种巧妙方法是使用Graphviz或NetworkX等图形包将它们描述为有向加权图。

        我们将在这里使用 Graphviz，因此您需要安装软件包才能跟进：

pip install graphviz==0.13.2

        值得浏览简短而甜蜜的官方安装指南，以确保您正确设置了软件包，特别是对于可能需要执行一些其他安装步骤的 Windows 用户。

        设置 Graphviz 后，创建一些用于绘图的辅助函数：

from graphviz import Digraph

# Define functions to visualize transition matrices as graphs

def get_df_edgelist(df, ls_index):
    ''' Derive an edge list with weight values
    '''
    edgelist = []
    for i in ls_index:
        for j in ls_index:
            edgelist.append([i, j, df[j][i]])
    return pd.DataFrame(edgelist, columns=['src', 'dst', 'weight'])

def edgelist_to_digraph(df_edgelist):
    ''' Convert an edge list into a weighted directed graph
    '''
    g = Digraph(format='jpeg')
    g.attr(rankdir='LR', size='30')
    g.attr('node', shape='circle')
    nodelist = []
    for _, row in df_edgelist.iterrows():
        node1, node2, weight = [str(item) for item in row]
        if node1 not in nodelist:
            g.node(node1, **{'width': '1', 'height': '1'})
            nodelist.append(node1)
        if node2 not in nodelist:
            g.node(node2, **{'width': '1', 'height': '1'})
            nodelist.append(node2)
        g.edge(node1, node2, label=weight)
    return g

def render_graph(fname, df, ls_index):
    ''' Render a visual graph and saves it to disk
    '''
    df_edgelist = get_df_edgelist(df, ls_index)
    g = edgelist_to_digraph(df_edgelist)
    g.render(fname, view=True)

现在，您可以生成每个转移矩阵。默认情况下，输出的图形将存储在您的工作目录中。

# Generate graph of transition matrix (raw co-occurrences)
render_graph('adjmat', df, ls_index)

# Generate graph of row-normalized transition matrix
render_graph('transmat_rnorm', df_rnorm, ls_index)

# Generate graph of column-normalized transition matrix
render_graph('transmat_cnorm', df_cnorm, ls_index)

        原始共现：

        行归一化转移概率：

        列归一化转移概率：

五、实际应用

5.1描述性见解

        我们可以对过渡矩阵做的第一件事也是最明显的事情是仅通过检查矩阵及其可视化图形表示来获得描述性见解。例如，通过上一节中示例的输出，我们可以收集如下高级见解：

• 在 9 个可能的事件转换中，有 3 个从未在我们的样本中发生（平坦→平坦、向下→向下和向下→平坦）。连续横盘事件的低概率可能表示时间序列数据正在跟踪的系统存在波动性。
• up 事件是唯一具有连续发生非零概率 （0.4） 的事件类型。事实上，这种转变概率是我们数据中最高的概率之一，可能表明数据基础系统中的强化效应。
• 在我们的例子中，基于行和基于列的归一化会产生不同的矩阵，尽管有一些重叠。这告诉我们，我们的时间序列在时间上本质上是不对称的，也就是说，我们看到的模式有些不同，这取决于我们是从给定的参考点回顾还是向前看。

5.2 预测和回溯

        通过将过渡矩阵的副本链接在一起，我们可以生成事件在时间上向前和向后发生的概率;这可以分别称为预测和反向预测。这里的一个中心假设是“历史无关紧要”;无论我们以什么时间步长 T 作为参考点，我们假设转移矩阵给出了 T+1（如果行归一化）和 T-1（如果列归一化）的相关概率。结果是，我们可以使用过渡矩阵从任意时间步进行预测和回溯。特别是，我们可以使用行规范化过渡矩阵进行预测，使用列规范化过渡矩阵进行反向预报。

        采用上面示例中计算的矩阵，假设我们在时间步长 t = 25 处观察到一个向上事件，并且我们希望预测哪个事件最有可能在时间步长 t = 27 发生。通过检查行归一化转移矩阵的第一行，我们直接看到，在下一个时间步长t = 26，观察到向上，横盘和向下事件的概率分别为0.4，0.4和0.2。为了推导出时间步长 t = 27 的类似事件概率（即，从我们的参考点开始的两个时间步长），我们需要将转移矩阵本身相乘，如下所示：

        请注意事件概率相对于我们的参考时间步长是如何变化的。例如，给定一个向上事件在t = 25时，观察到另一个上升事件的概率在t = 0时为4.26（向未来一步），在t = 0（向未来两步）时增加到56.27。 同时，在t = 0时观察到横盘事件的概率也是4.26，但在t = 0时降低到16.27。至关重要的是，这种矩阵乘法方法支持预测和回播。通常，为了预测或反向预测 n 次方之外的事件概率，我们可以分别计算行归一化或列归一化过渡矩阵到 n 次方。

        转移矩阵还可用于预测原始基础时间序列数据。让我们假设一个上升或下降事件相当于时间序列数据中的单个变化单位。现在假设时间序列在 t = 1 时从 2 上升到 25（向上事件），我们希望预测时间序列在 t = 26 和 t = 27 处的进展。 在上升事件之后，上升和横盘事件在t = 0时发生的可能性最高（4.26）。因此，我们可以预测，在 t = 26 时，时间序列很可能是 [1， 2， 3] 或 [1， 2， 2]，这两者都可能在 t = 27 时分别产生两种可能性：[1， 2， 3] 导致 [1， 2， 3， 4] 或 [1， 2， 3， 3]（概率各为 0.4，和以前一样）， 和 [1， 2， 2] 导致 [1， 2， 2， 3] 或 [1， 2， 2， 1]（每个概率为 0.5）。通常，我们期望用于生成转移矩阵的数据集越大、越丰富，在潜在事件链方面捕获的方差就越大，因此逐步预测精度就越高。

        转移矩阵的乘法链导致原始事件转移概率的日益复杂但完全可分解的组合。这种可分解性可以帮助我们更深入地了解构成时间序列数据（或随机过程）的事件的相互依赖性。

5.3 收敛分析

        将转移矩阵链接在一起的概念自然会引出一个有趣的问题：转移矩阵 M 的概率会收敛吗？具体来说，是否存在稳定的过渡矩阵 M*，使得 MM*=M*？如果是这样，那么 lim（n → ∞）Mⁿ = M*，即，我们期望由矩阵乘法链 Mⁿ 表示的马尔可夫过程在某个时间点收敛到稳定状态 M*;在这种情况下，该过程是收敛的，因此是稳定的。假设我们的转移矩阵是行规范化的，元素 M*（i， j） 为我们提供了事件 i 后跟事件 j 的稳定长期概率。但是，如果找不到稳定的矩阵 M*，则该过程是非收敛和不稳定的。

        使用前面几节中的运行示例，我们可以简要地勾勒出如何解析马尔可夫过程的收敛性。

        首先，我们假设有一个稳定的转移矩阵 M*，使得 MM*=M*，并且 M 是行归一化的。既然我们知道 M 是什么样子的，我们可以写出矩阵乘法如下：

        然后我们有以下线性方程组：

        如果这个方程组存在一个解（我们可以使用高斯消除等方法进行检查），那么我们也可以推导出一个收敛且稳定的转移矩阵。

六、包装

        一旦掌握了窍门，使用马尔可夫转移矩阵重构时间序列数据可以成为数据科学工具包的有用部分。正如您通常使用折线图可视化时间序列数据以更好地了解整体趋势一样，过渡矩阵提供了高度压缩但在其用例中通用的数据的补充表示形式。当可视化为有向图时，转移矩阵已经可用于获得高级描述性见解。当嵌入到更大的工作流中时，过渡矩阵可以构成更复杂的预测和回溯方法的基础。此外，虽然我们在上述部分中运行的简单示例将转移矩阵视为静态实体，但我们可以为不同的时间间隔推导出不同的矩阵;这在分析时间序列数据时特别有用，这些数据显示由数据中显著的 U 形或肘形模式反映的明显趋势反转。显然，上面讨论的想法有几个可能的扩展，所以继续尝试它们 - 它们可能会在你的下一个数据科学项目中派上用场。

参考资料：Time Series Data and Markov Transition Matrices | Towards Data Science