时序分析 43 -- 时序数据转为空间数据 (二) 马尔可夫转换场
马尔可夫转换场(MRF,Markov Transition Fields)
MRF
马尔可夫转换场(MRF, Markov Transition Fields)比GAF要简单一些,其数学模型对于从事数据科学的工程师来说也并不陌生,诸如马尔可夫模型或隐含马尔可夫模型(HMM)也是我们经常会用到的建模方法,在自然语言处理、机器学习等数据科学任务中也会经常遇到。
我们假设一个长度为 N N N 的时序数据,第一步我们把每一个值放到一个分位数中,例如,如果我们使用四分位数,那么就是把所以的值放置到其属于的分位桶中,25%,50%,75%,100%。这有点类似于直方图中的bin值。我们可以把每一个桶想象成马尔可夫模型中的一种状态。
马尔可夫状态转移矩阵
接下来,我们构造马尔可夫状态转移矩阵:
A i j = P ( s t = j ∣ s t − 1 = i ) A_{ij} = P(s_t = j | s_{t-1} = i) Aij=P(st=j∣st−1=i)
记得这里的 A i j A_{ij} Aij 代表从状态 i i i 转到状态 j j j 的转移概率,如果我们用 Q Q Q 分位数,那么这个矩阵就是 Q × Q Q \times Q Q×Q
通常情况下,我们会采用最大似然法来估计转移概率,简单来说 A i j A_{ij} Aij 可以用从状态 i i i 到 j j j 的计数除以状态 i i i 的次数或者是计数矩阵进行规范化。可以看到,从原时序数据转化来的马尔可夫状态转移矩阵对于原数据的分布不太敏感,并且丢失了时间信息,这并不是一个好事。所以MTF浮出水面。
MTF,马尔可夫转换场
MTF,即马尔可夫转换场,记作 M M M ,是一个 N × N N \times N N×N 矩阵, N N N 为时序长度:
M k l = A q k q l M_{kl} = A_{q_k q_l} Mkl=Aqkql
其中, q k q_k qk 是 x k x_k xk 的分位桶, q l q_l ql 是 x l x_l xl 的分位桶, x x x 为时序数据。
MTF 形如:
M = [ w i , j ∣ x 1 ∈ q i , x 1 ∈ q j w i , j ∣ x 1 ∈ q i , x 2 ∈ q j … w i , j ∣ x 1 ∈ q i , x n ∈ q j w i , j ∣ x 2 ∈ q i , x 1 ∈ q j w i , j ∣ x 2 ∈ q i , x 2 ∈ q j … w i , j ∣ x 2 ∈ q i , x n ∈ q j … … … … w i , j ∣ x n ∈ q i , x 1 ∈ q j w i , j ∣ x n ∈ q i , x 2 ∈ q j … w i , j ∣ x n ∈ q i , x n ∈ q j ] M = \begin{bmatrix} w_{i,j|x_1\in q_i,x_1\in q_j} & w_{i,j|x_1\in q_i,x_2\in q_j} & … & w_{i,j|x_1\in q_i,x_n\in q_j} \\ w_{i,j|x_2\in q_i,x_1\in q_j} & w_{i,j|x_2\in q_i,x_2\in q_j}& … & w_{i,j|x_2\in q_i,x_n\in q_j} \\ … & … & … & … \\w_{i,j|x_n\in q_i,x_1\in q_j} & w_{i,j|x_n\in q_i,x_2\in q_j} & … & w_{i,j|x_n\in q_i,x_n\in q_j}\end{bmatrix} M=⎣ ⎡wi,j∣x1∈qi,x1∈qjwi,j∣x2∈qi,x1∈qj…wi,j∣xn∈qi,x1∈qjwi,j∣x1∈qi,x2∈qjwi,j∣x2∈qi,x2∈qj…wi,j∣xn∈qi,x2∈qj…………wi,j∣x1∈qi,xn∈qjwi,j∣x2∈qi,xn∈qj…wi,j∣xn∈qi,xn∈qj⎦ ⎤
注意这里的 M M M 和 A A A 是不一样的 , A A A 中的下表是状态,而 M M M 中的下标是时序数据中的时间。相对于 A A A 的意义来讲, M k l M_{kl} Mkl 是 x k x_k xk 所在的分位桶转移到 x l x_l xl 所在的分位桶的概率。如下这种表示可能比较容易理解:
M i , j ∣ ∣ i − j ∣ = k M_{i,j||i-j|=k} Mi,j∣∣i−j∣=k 表示了时间间隔为 k k k 个点的转移概率,例如 M i j ∣ j − i = 1 M_{ij|j-i=1} Mij∣j−i=1 就表示在时间轴上相差一步的转移概率。对角线上 M i i M_{ii} Mii 是一种特殊情况,它意味着 ( k = 0 k=0 k=0 )在时间点 i i i 每一个分位桶转移到自身的概率。
MTF表示了时序数据中的任意两个时间点的数据之间的关系,相对的给出了它们之间从状态上看是否经常相邻。
MTF 聚合压缩
有的时候,我们希望能够压缩MTF矩阵的尺寸,尤其是MTF应用于可视化的时候。最常用的方法是对MTF图像中的像素进行求平均聚合运算,就是对每一个非重叠的 m × m m\times m m×m 窗口使用模糊核(blurring kernel) { 1 m 2 } m × m \{\frac{1}{m^2}\}_{m\times m} {m21}m×m进行平均。这种操作可以理解为对每一个长度为 m m m 的序列的转换概率进行聚合运算。
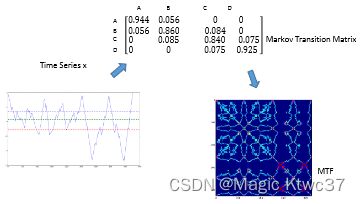
下图简单解释了MTF的整个过程: