【李沐】3.2线性回归从0开始实现

%matplotlib inline
import random
import torch
from d2l import torch as d2l

1、生成数据集：
看最后的效果，用正态分布弄了一些噪音

上面这个具体实现可以看书，又想了想还是上代码把：

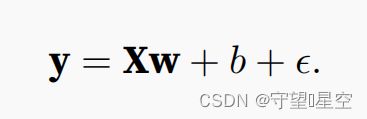
按照上面生成噪声，其中最后那个代表服从正态分布的噪声

def synthetic_data(w, b, num_examples):  # 定义函数 synthetic_data，接受权重 w、偏差 b 和样本数量 num_examples 作为参数
    """生成 y = Xw + b + 噪声 的合成数据集"""
    
    # 生成一个形状为 (num_examples, len(w)) 的特征矩阵 X，其中的元素是从均值为 0、标准差为 1 的正态分布中随机采样得到
    X = torch.normal(0, 1, (num_examples, len(w)))
    
    # 计算目标值 y，通过将特征矩阵 X 与权重 w 相乘，然后加上偏差 b，模拟线性回归的预测过程
    y = torch.matmul(X, w) + b
    
    # 给目标值 y 添加一个小的随机噪声，以模拟真实数据中的噪声。噪声从均值为 0、标准差为 0.01 的正态分布中随机采样得到
    y += torch.normal(0, 0.01, y.shape)
    
    # 返回特征矩阵 X 和目标值 y（将目标值 y 重塑为列向量的形式）
    return X, y.reshape((-1, 1)
# 定义真实的权重 true_w 为 [2, -3.4]
true_w = torch.tensor([2, -3.4])

# 定义真实的偏差 true_b 为 4.2
true_b = 4.2

# 调用 synthetic_data 函数生成合成数据集，传入真实的权重 true_w、偏差 true_b 和样本数量 1000
# 这将返回特征矩阵 features 和目标值 labels
features, labels = synthetic_data(true_w, true_b, 1000)

2、读取数据集
注意一般情况下要打乱。
下面函数的作用是该函数接收批量⼤⼩、特征矩阵和标签向量作为输⼊，⽣成⼤⼩为batch_size的⼩批量。每个⼩批量包含⼀组特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)  # 获取样本数量
    indices = list(range(num_examples))  # 创建一个样本索引列表，表示样本的顺序
    
    # 将样本索引列表随机打乱，以便随机读取样本，没有特定的顺序
    random.shuffle(indices)
    
    # 通过循环每次取出一个批次大小的样本
    for i in range(0, num_examples, batch_size):
        # 计算当前批次的样本索引范围，确保不超出总样本数量
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        
        # 通过索引获取对应的特征和标签，然后通过 yield 返回这个批次的数据
        # yield 使得函数可以作为迭代器使用，在每次迭代时产生一个新的批次数据
        yield features[batch_indices], labels[batch_indices]

3、初始化模型参数
第一步：前面两行代码，，我
们通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重，并将偏置初始化为0。
计算梯度使用2.5节引入的自动微分

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

4、定义模型
这里注意b是一个标量和向量相加，咋办？
前面说过向量的广播机制，就相当于是加到每一个上面

def linreg(X, w, b): #@save
"""线性回归模型"""
return torch.matmul(X, w) + b

5、定义损失函数
y.reshape(y_hat.shape))啥意思？
y_hat是真实值，这里的意思是弄成和y_hat相同的大小

def squared_loss(y_hat, y): #@save
"""均⽅损失"""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

6、优化算法
问：这里的参数是啥参数？params
更新完的参数不用返回吗？
为什么需要梯度清零？

def sgd(params, lr, batch_size):  # 定义函数 sgd，接受参数 params、学习率 lr 和批次大小 batch_size
    """小批量随机梯度下降"""
    
    with torch.no_grad():  # 使用 torch.no_grad() 来关闭梯度跟踪，以减少内存消耗
    
        for param in params:  # 遍历模型参数列表
            param -= lr * param.grad / batch_size  # 更新参数：参数 = 参数 - 学习率 * 参数梯度 / 批次大小
            param.grad.zero_()  # 清零参数的梯度，以便下一轮梯度计算

7、训练
问：反向传播是为了干啥？
是为了计算梯度，那梯度是啥呢
梯度是参数更快收敛的方向（就是向量）
优化方法是干啥的？
优化方法就是根据上面传过来的梯度，计算参数更新
所以，这几章看完后需要梳理深度学习的整个过程，以及每块有哪些方法，这些方法的特点和用那种方法更好
问（1）每个epoch训练多少数据？
整个训练集
（2）损失函数是啥？
损失函数是用来计算真实值域预测值之间的距离，当然是距离越小越好，可以拿均方误差想一下
（3）l.sum().backward()是啥意思？
看注释，补充：.backward() 方法用于执行自动求导，计算总的损失值对于模型参数的梯度。这将会构建计算图并沿着图的反向传播路径计算梯度。
（4）但是上面所说的梯度保存在哪里呢？
w.grad 和 b.grad 中
（5）但是sgd中也没有用到w.grad 啊？
用到了，param 可以是 w 或者 b，而 param.grad 则是相应参数的梯度。
（6）新问题：train_l = loss(net(features, w, b), labels)不是在前面已经计算过损失函数了吗？为啥在这里还需要计算？
前面计算损失函数是间断性的，目的是更新模型参数。
后面仍然计算的目的是根据更新完的参数对模型在整个训练集上与真实标签的差距做一个评估。

lr = 0.03  # 设置学习率为 0.03，控制每次参数更新的步幅

num_epochs = 3  # 设置训练的轮次（迭代次数）为 3，即遍历整个数据集的次数

net = linreg  # 定义模型 net，通常表示线性回归模型

loss = squared_loss  # 定义损失函数 loss，通常为均方损失函数，用于衡量预测值与真实值之间的差距
for epoch in range(num_epochs):  # 迭代 num_epochs 轮，进行训练

    for X, y in data_iter(batch_size, features, labels):  # 遍历数据集的每个批次
        
        l = loss(net(X, w, b), y)  # 计算当前批次的损失值 l，表示预测值与真实值之间的差距
        
        # 因为 l 的形状是 (batch_size, 1)，而不是一个标量。将 l 中的所有元素加起来，
        # 并计算关于 [w, b] 的梯度
        l.sum().backward()
        
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数，执行随机梯度下降算法
        
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)  # 在整个训练集上计算损失值
        
        # 打印当前迭代轮次和训练损失值的均值
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

8、练习中的问题

1. 如果我们将权重初始化为零，会发⽣什么。算法仍然有效吗？
   无效，为啥？因为，不同的X输入是相同的输出