二分查找
二分查找算法
描述
二分查找也称折半查找(Binary Search),它是一种效率非常高效的查找方法。但是折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
那它的效率有多高呢?还在给一个直观的数据做个展示吧,在一个1到2亿的个有充数组内查找一个给定值,使用二分查找需要多少次呢?最多也只需要28次。
##时间复杂度
二分查找的时间复杂非常的高,那高效到什么程序呢?
假设数据大小是n,每次查找都会缩小为原来的一半,即为除2操作,最坏情况下,直到查找区间缩小为空,才停止
被查找到的大小区间变化为
n,n/2,n/4,n/8,…,n/(2的k次方)
这是一个等比数列,n/(2的k次方)=1,可求得k=log2n,所以时间复杂度为O(logn)
logn是一种非常恐怖的数量数量级,即便n非常大,logn也很小,
比如2的30次方大约是10亿,在这10亿个数中使用二分查找,最多也就30次。
举个粟子
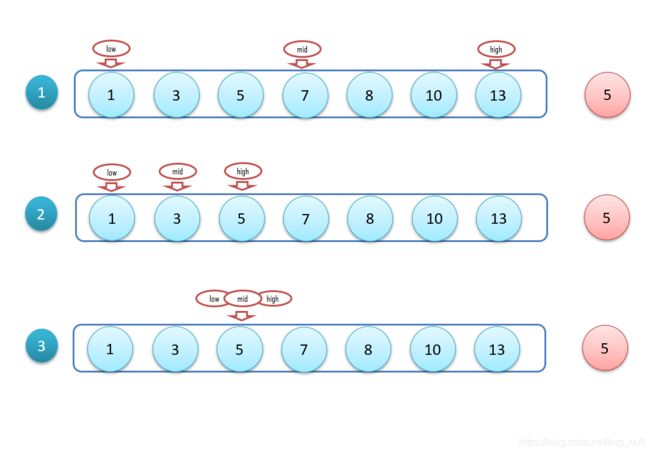
以“1,3,5,7,8,10,13”这组数据为例
public class BinarySearch {
/**
* 最简单的二分查找情况,在无重复的元素中去查找给定值
*
* @param data
* @param value
* @return
*/
public int search(int[] data, int value) {
if (null == data || data.length == 0) {
return -1;
}
int low = 0, mid, high = data.length - 1;
while (low <= high) {
mid = low + (high - low) / 2;
// 如果当前中间值等于组定值,则返回
if (data[mid] == value) {
return mid;
}
// 如果当前中间值大于组定值,说明在左区间查找
else if (data[mid] > value) {
high = mid - 1;
}
// 如果当前中间小于给定值,则说明在右区间查找
else {
low = mid + 1;
}
}
return -1;
}
}
二分查找的变体问题
变体1,查找每个值等于给定值的元素。
之前的数据中是不允许重复的,但在真实的数据中,数据是会存在重复的。
现在的问题就变成了,在一个出现重复的元素中,查找给定值。
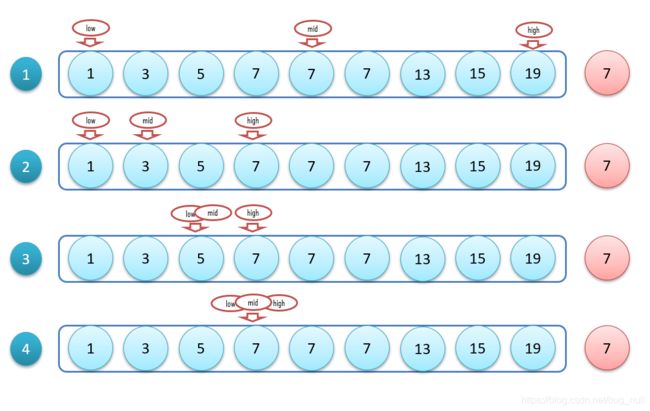
以数组“1,3,5,7,7,8,10,13”,查找第一个出现7的为例。
public class BinarySearchFirst {
/**
* 在一个重复的数组内,查找值等于给定值的元素,重复需要返回第一个
*
* @param data
* @param value
* @return
*/
public int search(int[] data, int value) {
if (null == data || data.length == 0) {
return -1;
}
int low = 0, mid, high = data.length - 1;
while (low <= high) {
mid = low + (high - low) / 2;
// 当查找到当前元素为给定元素
if (data[mid] == value) {
// 由于存在重复,需在检查是否为第一次出现
//为0,则肯定为首次出现,前一个元素不与当前元素相同,也说明首次出现
if (mid == 0 || data[mid - 1] != value) {
return mid;
}
// 非第一次出现,继续向左搜索
else {
high = mid - 1;
}
}
// 如果当前值中间值大于给定值,则在左区间查找
else if (data[mid] > value) {
high = mid - 1;
}
// 如果当前中间件小于给定值,则在右区间搜索
else {
low = mid + 1;
}
}
return -1;
}
}
变体2,查找最后一个值等于给定值的元素
以数组“1,3,5,7,7,8,10,13”,查找最后一个出现7的为例。
public class BinarySearchLast {
/**
* 在一个重复的数组内,查找最后一个值等于给定值的元素
*
* @param data
* @param value
* @return
*/
public int search(int[] data, int value) {
if (null == data || data.length == 0) {
return -1;
}
int low = 0, mid, high = data.length - 1;
while (low <= high) {
mid = low + (high - low) / 2;
// 1,如果区间中间件等于查找到的值
if (data[mid] == value) {
// 如果已经为最后值,说明为最后一个,
// 如果后一个元素与给定值不同,也说明为最后一个
if (data[mid] == high || data[mid + 1] != value) {
return mid;
}
// 如果非最后一个,则在右区间继续查找
else {
low = mid + 1;
}
}
// 如果区间中间值大于给定值,则说明需要继续在左区间查找
else if (data[mid] > value) {
high = mid - 1;
}
// 区间中间值小于给定值,则需要继续右区间中查找
else {
low = mid + 1;
}
}
return -1;
}
}
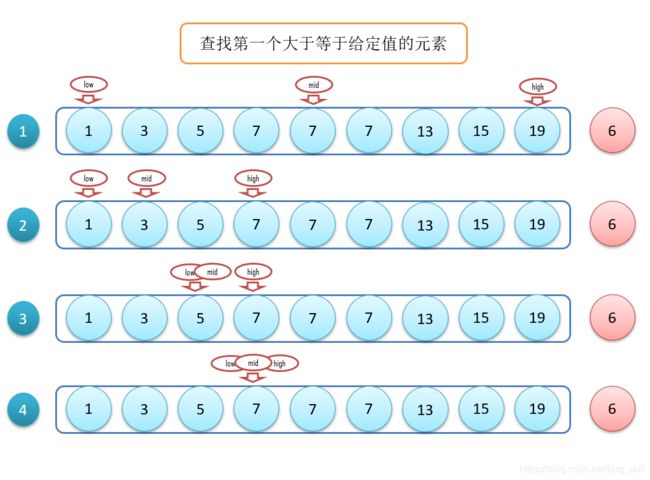
变体3,查找每个大于等于组定的元素
以数组“1,3,5,7,7,8,10,13”,查找最后一个出现7的为例。
public class BinarySearchEqualOrGreaterThan {
/**
* 查找第一个大于等于给定值的元素
*
* @param data
* @param value
* @return
*/
public int search(int[] data, int value) {
if (null == data || data.length == 0) {
return -1;
}
int low = 0, mid, high = data.length - 1;
while (low <= high) {
mid = low + (high - low) / 2;
// 当前区间中间值如果大于等于给定值
if (data[mid] >= value) {
// 如果为首元素或者前一个元素小于给定元素,则结束
if (mid == 0 || data[mid - 1] < value) {
return mid;
}
// 否则继续向左区间查找
else {
high = mid - 1;
}
}
// 如果当前区间中间值小于给定值,则在右区间查找
else {
low = mid + 1;
}
}
return -1;
}
}
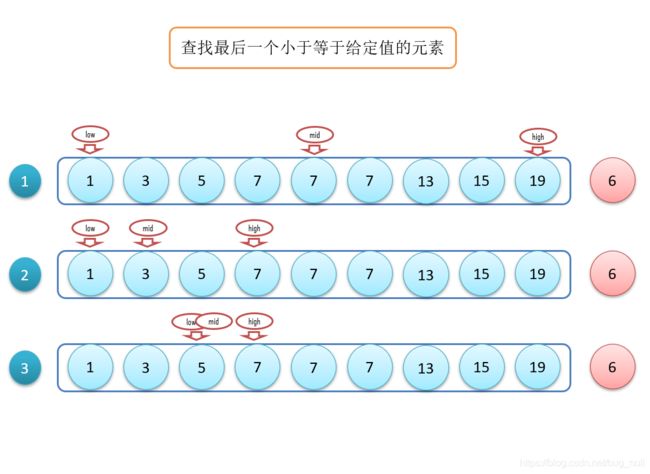
变体4,查找最后一个小于等于给定值的元素
以数组“1,3,5,7,7,8,10,13”,查找最后一个出现7的为例。
public class BinarySearchEqualOrLessThan {
/**
* 查找最后一个小于等于给定值的元素
*
* @param data
* @param value
* @return
*/
public int search(int[] data, int value) {
if (null == data || data.length == 0) {
return -1;
}
int low = 0, mid, high = data.length - 1;
while (low <= high) {
mid = low + (high - low) / 2;
// 如果当前区间中间值小于等于给定值
if (data[mid] <= value) {
// 如果当前为最后一个,则直接返回
// 或者当前区间中间值的后一个元素大于给定元素,也返回
if (mid == high || data[mid + 1] > value) {
return mid;
}
// 否则继续在右区间继续查找
else {
low = mid + 1;
}
}
// 如果当前区间中间值大于给定值,则在左区间中查找
else {
high = mid - 1;
}
}
return -1;
}
}
关于二分查找的处理注意事项
二分查找算法写起来非常的烧脑,很容易因为细节处理不好而产生bug,
容易出现的错误:终点条件,区间上下界更新方法,返回值选择。