代码随想录(一)数组
二 二分查找:
1 [ ]
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() -1;
while (left <= right) {
int middle = left + ((right - left)/2);
if (nums[middle] > target) {
right = middle - 1;
} else if (nums[middle] < target) {
left = middle + 1;
} else {
return middle;
}
}
return -1;
}
};
2 [ ) 记住不是两边都开 所以左区间右区间解法不一样
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size();
while (left < right) {
int middle = left + ((right - left)/2);
if (nums[middle] > target) {
right = middle;
} else if (nums[middle] < target) {
left = middle + 1;
} else {
return middle;
}
}
return -1;
}
};
三 移除元素
1 暴力解法 O(n^2)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int size = nums.size();
for ( int i = 0 ; i < size; i++){
if (nums[i] == val) {
for ( int j = i+1; j < size; j++) {
nums[j-1] = nums[j];
}
i--; //先i-- 因为外层循环结束一次后会自动i++
size --;
}
}
return size;
}
};
2 双指针 O(n)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if(nums[fastIndex] != val){ //不等才需要更新新数组
nums[slowIndex] = nums[fastIndex];
slowIndex++;
}
}
return slowIndex; //慢指针所指向的数组下标就是新数组的长度
}
};
四 有序数组的平方
双指针
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int k = nums.size()-1; //k从右往左移动的
vector<int> result(nums.size(),0);
for(int i = 0, j = nums.size()-1; i <= j; ) { // 不能漏掉i=j的情况 第二个;后不能写i++,j-- 不是每次循环都会这么做
if (nums[i] * nums[i] < nums[j]*nums[j]) {
result[k] = nums[j]*nums[j];
k--;
j--;
}
else { //>=
result[k] = nums[i]*nums[i];
k--;
i++;
}
}
return result;
}
};
1 暴力解法: O(n^2) 力扣会超出时间限制
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0; //子序列的数值之和
int sublength = 0; //子序列的长度
for(int i = 0; i < nums.size(); i++) //确定子序列的起始位置
{
sum = 0; //每次循环重新把sum置为0
for(int j = i; j < nums.size(); j++) {
sum += nums[j];
if(sum>= target) { //>=才有必要算长度
sublength = j-i+1;
result = sublength < result ? sublength:result;
break;//往后遍历只会越长
}
}
}
return result == INT32_MAX ? 0 : result;
}
};
2 滑动窗口(双指针) O(n)
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int sum = 0;
int sublength = 0;
int result = INT32_MAX;
int i = 0;
for(int j=0; j < nums.size(); j++) {
sum += nums[j]; //每次把快指针的元素加进来
// if(j>i){ 这个j i 不用判断的 因为减去慢指针指向的数据 就会不满足 sum >= s
while (sum >= target) { //不能用if 如果满足条件 慢指针会持续往前移动
sublength = j-i+1;
result = sublength < result? sublength : result;
sum -= nums[i];
i++;
}
}
return result == INT32_MAX ? 0 : result;
}
};
下面这位的讲解有助于理解
leetcode209.长度最小的子数组
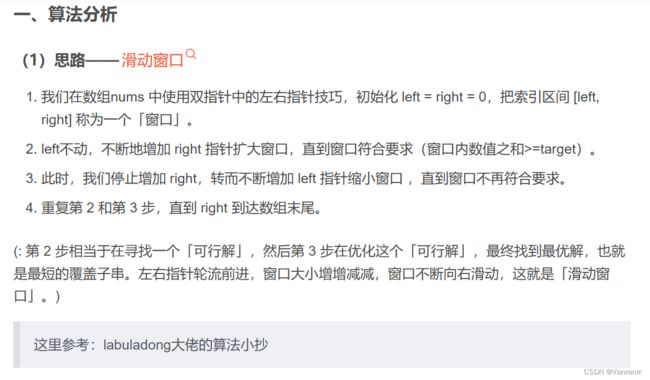

他的代码:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int numsSize = nums.size();
if (numsSize == 0) return 0;//判断数组是否为空
int resMin = INT_MAX;
/*
resMin表示最终取的符合条件的最短的子数组长度.
INT_MAX是C++中的常量,表示int型的最大值,包含在头文件limits.h中.
这样才能不断更新取所有窗口长度的最小值
*/
int left = 0, right = 0;
//左右指针,滑动窗口的左右两端
int sum = 0, subLen = 0;
//窗口数值之和, 窗口的长度
while (right < numsSize) {
//left不变,right右移扩大窗口,直到满足要求进入下面的while循环
sum += nums[right];
//满足要求之后left右移缩小窗口优化这个解,直到不满足要求
while (sum >= target) {
subLen = right - left + 1;
//先计算出当前滑动窗口的长度
//再和resMin作比较,若sublen更小则更新resMin
resMin = subLen < resMin ? subLen : resMin;
//也可以写成resMin = min(subLen, resMin);
sum -= nums[left++];
}
right++;
//若此时窗口不满足要求(不会进入while循环)则right++扩大窗口
//若满足要求找到一个优化解之后right右移继续往后找更多解
}
return resMin == INT_MAX ? 0 : resMin;
//若resMin未改变说明数组中不存在符合条件的子数组
}
};