【排排站:探索数据结构中的队列奇象】
本章重点
队列的概念及结构
队列的实现方式
链表方式实现栈接口
队列面试题
一、队列的概念及结构
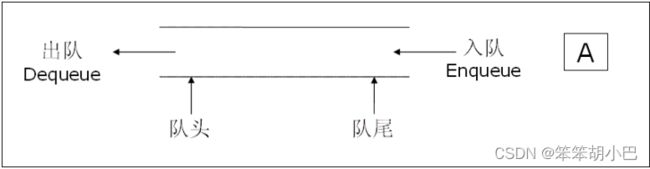
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 FIFO(First In First Out)
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
- 队头:线性表允许删除的那一端。
- 队尾:线性表允许插入的那一端。
- 空队:不含任何元素的空表。
二、队列的实现方式
如图3-5所示为依次向队列中插入元素 a0,a1,…,an-1后的示意图,其中,a0是当前队头元素,an-1 是当前队尾元素。
就像在食堂买饭就餐一样,如果你在就餐人不多时去食堂就餐,你一到买饭窗口就能得到食堂服务人员的服务;但如果你在就餐人很多时去食堂就餐,你就需要在某个窗口排队等待,直到轮到你时才能得到食堂服务人员的服务。在软件设计中也经常会遇到需要排队等待服务的问题。队列可用于临时存储那些需要等待接受服务的信息序列。
队列只允许在头部插入,尾部删除,因此队列的实现一般可以使用数组或者链表实现。
1.顺序队列
 如图3-6所示为一个有6个内存单元的顺序队列的动态示意图,图中front为队头指针,rear为队尾指针。图3-6 (a)表示一个空队列;图3-6 (b)表示A、B、C入队列后的状态;图3-6 (c) 为A、B出队列后的状态;图3-6 (d) 为D,E入队列后的状态。
如图3-6所示为一个有6个内存单元的顺序队列的动态示意图,图中front为队头指针,rear为队尾指针。图3-6 (a)表示一个空队列;图3-6 (b)表示A、B、C入队列后的状态;图3-6 (c) 为A、B出队列后的状态;图3-6 (d) 为D,E入队列后的状态。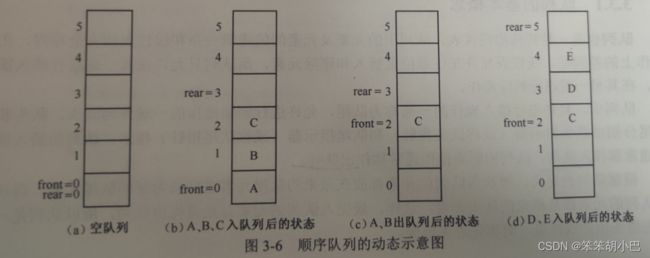
2.链式队列
我们已知,队列是操作受限制的线性表,队列有队头和队尾,插入元素的一端称为队尾,
删除元素的一端称为队头。
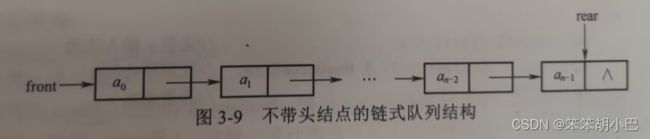
链式队列的队头指针指向队列的当前头结点位置,队尾指针指向队列的当前队尾结点位置。对于不带头结点的链式队列,出队列时可直接删除队头指针所指的结点,因此链式队列没有头结点更方便。一个不带头结点、队列中有元素a0,a1,…,an-1的链式队列的结构如图3-9所示,其中,指针 front 指示的是链式队列的队头结点,指针 rear 指示的是链式队列的队尾结点。
三、链表方式实现栈接口
由于队列只允许在头部插入,尾部删除,因此我们会改变头结点,前面我们学过用二级指针和返回值两种方式来处理头结点改变,今天我们来学一种新方式:结构体修改,将队列的头结点和尾结点放入到一个结构体当中,通过结构体地址就可以修改结构体的内容,同时还加入了一个size,用来计算当前队列的长度。
typedef int QDataType;
// 单链式结构:表示队列
typedef struct QListNode
{
struct QListNode* Next;
QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* front;
QNode* rear;
int size;
}Queue;
// 初始化队列
void QueueInit(Queue * q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空
bool QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);1.初始化队列:void QueueInit(Queue* q)
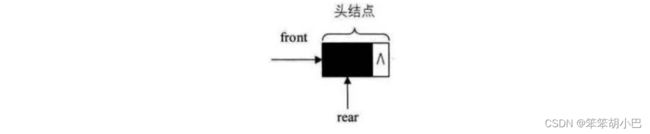
直接将front和rear域都设置为NULL,将队列长度设置为0,
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->front = q->rear = NULL;
q->size = 0;
}2.队尾入队列:void QueuePush(Queue* q, QDataType data)
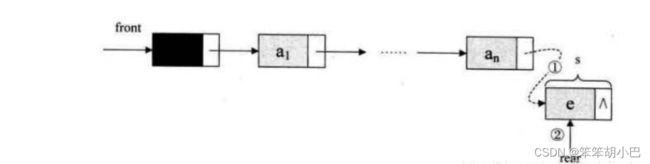
构造一个节点newnode,data域存储数据,next域存储NULL,若原链队为空,则将链队结点的两个域都指向结点newnode,否则将结点newnode链接到单链表末尾,并让链队结点的rear域指向它,再让队列的长度+1
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = data;
newnode->Next = NULL;
if (q->rear == NULL)
{
q->front = q->rear = newnode;
}
else
{
q->rear->Next = newnode;
q->rear = newnode;
}
q->size++;
}3.队头出队列:void QueuePop(Queue* q)
若原链队为空,则下溢,assert断言提示错误,否则将队首结点的Next域赋值给next,并删除队首结点,若原链队只有一个结点,则需要将链队结点的两个域都设置为NULL,表示此时链队已空。然后队列长度-1.
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
//队列为空,断言
assert(!QueueEmpty(q));
//rear出现野指针的问题
if (q->front->Next == NULL)
{
free(q->front);
q->front = q->rear = NULL;
}
else
{
QNode* next = q->front->Next;
free(q->front);
q->front = next;
}
q->size--;
}4.获取队列头部元素:QDataType QueueFront(Queue* q)
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
//队列为空,断言
assert(!QueueEmpty(q));
return q->front->data;
}5.获取队列队尾元素:QDataType QueueBack(Queue* q)
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
//队列为空,断言
assert(!QueueEmpty(q));
return q->rear->data;
}6.获取队列中有效元素个数:int QueueSize(Queue* q)
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}7.检测队列是否为空:bool QueueEmpty(Queue* q)
// 检测队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);
//头为空,该队列就为空
//返回true - 队列就为空
//返回false - 队列不为空
return q->front == NULL;
}8.销毁队列:void QueueDestroy(Queue* q)
销毁队列创建一个结点保存下个结点的值,释放当前结点,然后依次遍历队列,依次释放结点。释放后需要将队头和队尾都置空,队列长度设置为0,由于是通过结构体去修改头结点,此时队列已经为空指针,在调用函数后,不需要手动将头指针置空。
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
QNode* next = cur->Next;
free(cur);
cur = next;
}
q->front = q->rear = NULL;
q->size = 0;
}四、队列面试题
1. 用队列实现栈。OJ链接
- 栈是一种后进先出的数据结构,元素从顶端入栈,然后从顶端出栈。
- 队列是一种先进先出的数据结构,元素从后端入队,然后从前端出队。
思路:
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作,其中 queue1用于存储栈内的元素,queue2作为入栈操作的辅助队列。
入栈操作时,首先将元素入队到 queue2 ,然后将 queue1的全部元素依次出队并入队到 queue2此时 queue2的前端的元素即为新入栈的元素,再将 queue1和 queue2 互换,则 queue1 的元素即为栈内的元素,queue1的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保 queue1的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 queue1的前端元素并返回即可,获得栈顶元素操作只需要获得 queue1的前端元素并返回即可(不移除元素)。
由于 queue1用于存储栈内的元素,判断栈是否为空时,只需要判断 queue1是否为空即可。
typedef struct {
int* stk;
int stkSize;
int stkCapacity;
} Stack;
Stack* stackCreate(int cpacity) {
Stack* ret = malloc(sizeof(Stack));
ret->stk = malloc(sizeof(int) * cpacity);
ret->stkSize = 0;
ret->stkCapacity = cpacity;
return ret;
}
void stackPush(Stack* obj, int x) {
obj->stk[obj->stkSize++] = x;
}
void stackPop(Stack* obj) {
obj->stkSize--;
}
int stackTop(Stack* obj) {
return obj->stk[obj->stkSize - 1];
}
bool stackEmpty(Stack* obj) {
return obj->stkSize == 0;
}
void stackFree(Stack* obj) {
free(obj->stk);
}
typedef struct {
Stack* inStack;
Stack* outStack;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* ret = malloc(sizeof(MyQueue));
ret->inStack = stackCreate(100);
ret->outStack = stackCreate(100);
return ret;
}
void in2out(MyQueue* obj) {
while (!stackEmpty(obj->inStack)) {
stackPush(obj->outStack, stackTop(obj->inStack));
stackPop(obj->inStack);
}
}
void myQueuePush(MyQueue* obj, int x) {
stackPush(obj->inStack, x);
}
int myQueuePop(MyQueue* obj) {
if (stackEmpty(obj->outStack)) {
in2out(obj);
}
int x = stackTop(obj->outStack);
stackPop(obj->outStack);
return x;
}
int myQueuePeek(MyQueue* obj) {
if (stackEmpty(obj->outStack)) {
in2out(obj);
}
return stackTop(obj->outStack);
}
bool myQueueEmpty(MyQueue* obj) {
return stackEmpty(obj->inStack) && stackEmpty(obj->outStack);
}
void myQueueFree(MyQueue* obj) {
stackFree(obj->inStack);
stackFree(obj->outStack);
}
2. 用栈实现队列。OJ链接
将一个栈当作输入栈,用于压入 push\ 传入的数据;另一个栈当作输出栈,用于 pop 和 peek 操作。每次 pop 或 peek 时,若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。
typedef struct {
int* stk;
int stkSize;
int stkCapacity;
} Stack;
Stack* stackCreate(int cpacity) {
Stack* ret = malloc(sizeof(Stack));
ret->stk = malloc(sizeof(int) * cpacity);
ret->stkSize = 0;
ret->stkCapacity = cpacity;
return ret;
}
void stackPush(Stack* obj, int x) {
obj->stk[obj->stkSize++] = x;
}
void stackPop(Stack* obj) {
obj->stkSize--;
}
int stackTop(Stack* obj) {
return obj->stk[obj->stkSize - 1];
}
bool stackEmpty(Stack* obj) {
return obj->stkSize == 0;
}
void stackFree(Stack* obj) {
free(obj->stk);
}
typedef struct {
Stack* inStack;
Stack* outStack;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* ret = malloc(sizeof(MyQueue));
ret->inStack = stackCreate(100);
ret->outStack = stackCreate(100);
return ret;
}
void in2out(MyQueue* obj) {
while (!stackEmpty(obj->inStack)) {
stackPush(obj->outStack, stackTop(obj->inStack));
stackPop(obj->inStack);
}
}
void myQueuePush(MyQueue* obj, int x) {
stackPush(obj->inStack, x);
}
int myQueuePop(MyQueue* obj) {
if (stackEmpty(obj->outStack)) {
in2out(obj);
}
int x = stackTop(obj->outStack);
stackPop(obj->outStack);
return x;
}
int myQueuePeek(MyQueue* obj) {
if (stackEmpty(obj->outStack)) {
in2out(obj);
}
return stackTop(obj->outStack);
}
bool myQueueEmpty(MyQueue* obj) {
return stackEmpty(obj->inStack) && stackEmpty(obj->outStack);
}
void myQueueFree(MyQueue* obj) {
stackFree(obj->inStack);
stackFree(obj->outStack);
}
3. 设计循环队列。OJ链接
顺序队列的假溢出问题
解决假溢出的方法就是后面满了,就再从头开始,也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。当队首指针Q->front = MAXSIZE-1后,再前进一个位置就自动到0,这可以利用除法取余运算(%)来实现。
- 初始时:Q->front = Q->rear=0。
- 队首指针进1:Q->front = (Q->front + 1) % MAXSIZE。
- 队尾指针进1:Q->rear = (Q->rear + 1) % MAXSIZE。
- 队列长度:(Q->rear - Q->front + MAXSIZE) % MAXSIZE。
出队入队时,指针都按照顺时针方向前进1,如下图所示:
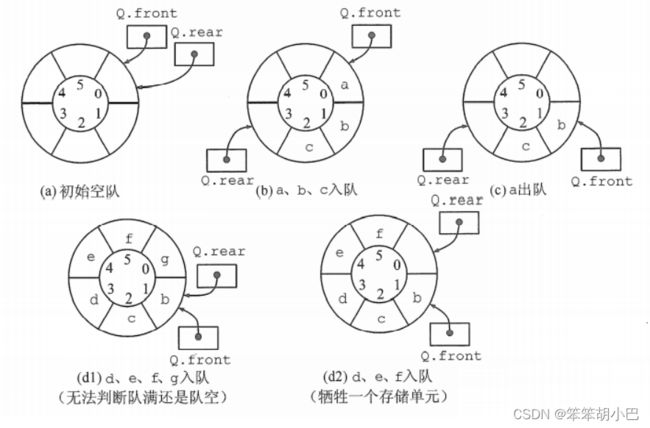
那么,循环队列队空和队满的判断条件是什么呢?
显然,队空的条件是 Q->front == Q->rear 。若入队元素的速度快于出队元素的速度,则队尾指针很快就会赶上队首指针,如图( d1 )所示,此时可以看出队满时也有 Q ->front == Q -> rear 。为了区分队空还是队满的情况,有三种处理方式:
(1)牺牲一个单元来区分队空和队满,入队时少用一个队列单元,这是种较为普遍的做法,约定以“队头指针在队尾指针的下一位置作为队满的标志”,如图 ( d2 )所示。
- 队满条件: (Q->rear + 1)%Maxsize == Q->front
- 队空条件仍: Q->front == Q->rear
- 队列中元素的个数: (Q->rear - Q ->front + Maxsize)% Maxsize
(2)类型中增设表示元素个数的数据成员。这样,队空的条件为 Q->size == O ;队满的条件为 Q->size == Maxsize 。这两种情况都有 Q->front == Q->rear
(3)类型中增设tag 数据成员,以区分是队满还是队空。tag 等于0时,若因删除导致 Q->front == Q->rear ,则为队空;tag 等于 1 时,若因插入导致 Q ->front == Q->rear ,则为队满。
typedef struct {
int front;
int rear;
int capacity;
int *elements;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue *obj = (MyCircularQueue *)malloc(sizeof(MyCircularQueue));
obj->capacity = k + 1;
obj->rear = obj->front = 0;
obj->elements = (int *)malloc(sizeof(int) * obj->capacity);
return obj;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if ((obj->rear + 1) % obj->capacity == obj->front) {
return false;
}
obj->elements[obj->rear] = value;
obj->rear = (obj->rear + 1) % obj->capacity;
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if (obj->rear == obj->front) {
return false;
}
obj->front = (obj->front + 1) % obj->capacity;
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if (obj->rear == obj->front) {
return -1;
}
return obj->elements[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if (obj->rear == obj->front) {
return -1;
}
return obj->elements[(obj->rear - 1 + obj->capacity) % obj->capacity];
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->rear == obj->front;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->rear + 1) % obj->capacity == obj->front;
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->elements);
free(obj);
}
本章结束啦!!!