思维进化算法(MEA)优化BP神经网络
随着计算机科学的发展,人们借助适者生存这一进化规则,将计算机科学和生物进化结合起来,逐渐发展形成一类启发式随机搜索算法,这类算法被称为进化算法(Evolutionary Com-putation, EC)。最著名的进化算法有:遗传算法、进化策略、进化规划。与传统算法相比,进化算法的特点是群体搜索。进化算法已经被成功地应用于解决复杂的组合优化问题、图像处理,人工智能、机器学习等领域。但是进化算法存在的问题和缺陷也不能忽视,如早熟、收敛速度慢等。
针对EC存在的问题,孙承意等人于1998年提出了思维进化算法(Mind Evolutionary Al-gorithm,MEA)。本章将详细介绍思维进化算法的基本思想,并结合非线性函数拟合实例,在MATLAB环境下实现思维进化算法。
1 案例背景
1.1思维进化算法概述
思维进化算法沿袭了遗传算法的一些基本概念,如“群体”、“个体”、“环境”等,其主要系统框架如图31- 1所示。
与遗传算法不同,思维进化算法的一些新的概念解释如下:
1)群体和子群体
MEA是一种通过迭代进行优化的学习方法,进化过程的每一代中的所有个体的集合成为一个群体。一个群体分为若干个子群体。子群体包括两类:优胜子群体(superior group)和临时子群体temporary group)。优胜子群体记录全局竞争中的优胜者的信息,临时子群体记录全局竞争的过程。
2)公告板
公告板相当于一个信息平台,为个体之间和子群体之间的信息交流提供了机会。公告板记录三个有效的信息:个体或子群体的序号、动作(action)和得分(score)。利用个体或子群体的序号,可以方便地区分不同个体或子群体;动作的描述根据研究领域不同而不同,例如本文是研究利用思维进化如何优化参数的问题,那么动作记录的就是个体和子群体的具体位置;得分是环境对个体动作的评价,在利用思维进化算法优化过程中,只有时刻记录每个个体和子群体的得分,才能快速地找到优化的个体和子群体。子群体内的个体在局部公告板(local bill-board)张贴各自的信息,全局公告板(global billboard)用于张贴各子群体的信息。
3)趋同
趋同(similartaxis)是 MEA中的两个重要概念之一,下面给出它的定义。
定义1:在子群体范围内,个体为成为胜者而竞争的过程叫做趋同。
定义2:一个子群体在趋同过程中,若不再产生新的胜者,则称该子群体已经成熟。当子群体成熟时,该子群体的趋同过程结束。子群体从诞生到成熟的期间叫做生命期。
4)异化
MEA 中的另一个重要概念是异化(dissimilation),它的定义是:
定义3:在整个解空间中,各子群体为成为胜者而竞争,不断地探测解空间中新的点,这个过程叫做异化。
异化有两个含义:
①各子群体进行全局竞争,若一个临时子群体的得分高于某个成熟的优胜子群体的得分,则该优胜子群体被获胜的临时子群体替代,原优胜子群体中的个体被释放;若一个成熟的临时子群体的得分低于任意一个优胜子群体的得分,则该临时子群体被废弃,其中的个体被释放。
②被释放的个体在全局范围内重新进行搜索并形成新的临时群体。
1.2 思维进化算法基本思路
MEA 的基本思路是:
①在解空间内随机生成一定规模的个体,根据得分(对应于遗传算法中的适应度函数值,表征个体对环境的适应能力)搜索出得分最高的若干个优胜个体和临时个体。
②分别以这些优胜个体和临时个体为中心,在每个个体的周围产生一些新的个体,从而得到若干个优胜子群体和临时子群体。
③在各个子群体内部执行趋同操作,直至该子群体成熟,并以该子群体中最优个体(即中心)的得分作为该子群体的得分。
④子群体成熟后,将各个子群体的得分在全局公告板上张贴,子群体之间执行异化操作,完成优胜子群体与临时子群体间的替换、废弃、子群体中个体释放的过程,从而计算全局最优个体及其得分。
值得一提的是,异化操作完成后,需要在解空间内产生新的临时子群体,以保证临时子群体的个数保持不变。
1.3思维进化算法特点
与遗传算法相比,思维进化算法具有许多自身的特点:
①把群体划分为优胜子群体和临时子群体,在此基础上定义的趋同和异化操作分别进行探测和开发,这两种功能相互协调且保持一定的独立性,便于分别提高效率,任一方面的改进都对提高算法的整体搜索效率有利。
②MEA可以记忆不止一代的进化信息,这些信息可以指导趋同与异化向着有利的方向进行。
③结构上固有的并行性。
④遗传算法中的交叉与变异算子均具有双重性,即可能产生好的基因,也可能破坏原有的基因,而MEA中的趋同和异化操作可以避免这个问题。
1.4 问题描述
利用BP神经网络建立非线性函数的回归模型。在训练BP神经网络前,利用思维进化算法对BP神经网络的初始权值和阈值进行优化。
2模型建立
2.1设计思路
利用思维进化算法对BP神经网络的初始权值和阈值进行优化。首先,根据BP神经网络的拓扑结构,将解空间映射到编码空间,每个编码对应问题的一个解(即个体)。这里,选择BP神经网络拓扑结构为2-5-1,编码长度为21。然后,选取训练集的均方误差的倒数作为各个个体与种群的得分函数,利用思维进化算法,经过不断迭代,输出最优个体,并以此作为初始权值和阈值,训练BP神经网络。
2.2设计步骤
根据上述设计思路,设计步骤主要包括以下几个部分,如图31-2所示。
1)训练集/测试集产生
与传统前馈神经网络相同,为了使得建立的模型具有良好的泛化性能,要求具有足够多的训练样本且具有较好的代表性。
2)初始种群产生
利用初始种群产生函数initpop_generate(),可以方便地产生初始种群。利用子种群产生函数subpop_generate(),可以方便地产生优胜子种群和临时子种群。具体用法请参考3.1和3.2节,此处不再赘述。
3)子种群趋同操作
优胜子种群和临时子种群产生后,各个子种群首先需要执行趋同操作,利用种群成熟判别函数 ismature(),可以方便地判断各个子种群趋同操作是否完成,具体用法请参考31.3.3节,此处不再赘述。
4)子种群异化操作
各个优胜子群体和临时子群体趋同操作完成后,便可以执行异化操作,并根据异化操作的结果,补充新的子群体,具体程序详见第4节。
5)解析最优个体
当满足迭代停止条件时,思维进化算法结束优化过程。此时,根据编码规则,对寻找到的最优个体进行解析,从而得到对应的BP神经网络的权值和阈值。
6)训练P神经网络
将优化得到的权值和阈值作为BP神经网络的初始权值和阈值,并利用训练集样本对BP神经网络进行训练.学习。
7)仿真预测、结果分析
与传统BP神经网络相同,训练完成后,便可输人测试集样本,进行仿真预测,并可以进行结果分析和讨论。
3 思维进化算法函数
为了方便读者学习,使用思维进化算法,笔者按照思维进化算法的基本思路,尝试编写了思维进化算法中的一些重要函数,下面将详细介绍它们的调用格式和具体函数内
initpop_generate()函数为初始种群产生函数,其调用格式为
initpop = initpop_generate(popsize,S1,S2,S3,P,T)
其中 , popsize为种群规模大小;S1为BP神经网络输入层神经元个数;S2为BP神经网络隐含层神经元个数;S3为BP神经网络输出层神经元个数;P为训练集样本输入矩阵;T为训练集样本输出矩阵;initpop为产生的初始种群。
initpop_generate.m函数文件的具体内容如下:
function initpop = initpop_generate(popsize,S1,S2,S3,P,T)
% 编码长度(权值/阈值总个数)
S = S1*S2 + S2*S3 + S2 + S3;
% 预分配初始种群数组
initpop = zeros(popsize,S+1);
for i = 1:popsize
% 随机产生一个个体[-1,1]
x = rand(1,S)*2 - 1;
% 前S1*S2个编码为W1(输入层与隐含层间权值)
temp = x(1:S1*S2);
W1 = reshape(temp,S2,S1);
% 接着的S2*S3个编码为W2(隐含层与输出层间权值)
temp = x(S1*S2+1:S1*S2+S2*S3);
W2 = reshape(temp,S3,S2);
% 接着的S2个编码为B1(隐含层神经元阈值)
temp = x(S1*S2+S2*S3+1:S1*S2+S2*S3+S2);
B1 = reshape(temp,S2,1);
%接着的S3个编码B2(输出层神经元阈值)
temp = x(S1*S2+S2*S3+S2+1:end);
B2 = reshape(temp,S3,1);
% 计算隐含层神经元的输出
A1 = tansig(W1*P,B1);
% 计算输出层神经元的输出
A2 = purelin(W2*A1,B2);
% 计算均方误差
SE = mse(T-A2);
% 思维进化算法的得分
val = 1 / SE;
% 个体与得分合并
initpop(i,:) = [x val];
end3.2子种群产生函数
subpop_generate()函数为子种群产生函数,其调用格式为:
subpop= subpop_generate(center,SG,S1,S2,S3 ,P,T)
其中, center为子种群的中心;SG为子种群的规模大小;S1为BP神经网络输入层神经元个数;S2为BP神经网络隐含层神经元个数;S3为BP神经网络输出层神经元个数;P为训练集样本输入矩阵;T为训练集样本输出矩阵;subpop为产生的子种群。
subpop_generate.m函数文件的具体内容如下:
function subpop = subpop_generate(center,SG,S1,S2,S3,P,T)
% 编码长度(权值/阈值总个数)
S = S1*S2 + S2*S3 + S2 + S3;
% 预分配初始种群数组
subpop = zeros(SG,S+1);
subpop(1,:) = center;
for i = 2:SG
x = center(1:S) + 0.5*(rand(1,S)*2 - 1);
% 前S1*S2个编码为W1(输入层与隐含层间权值)
temp = x(1:S1*S2);
W1 = reshape(temp,S2,S1);
% 接着的S2*S3个编码为W2(隐含层与输出层间权值)
temp = x(S1*S2+1:S1*S2+S2*S3);
W2 = reshape(temp,S3,S2);
% 接着的S2个编码为B1(隐含层神经元阈值)
temp = x(S1*S2+S2*S3+1:S1*S2+S2*S3+S2);
B1 = reshape(temp,S2,1);
%接着的S3个编码B2(输出层神经元阈值)
temp = x(S1*S2+S2*S3+S2+1:end);
B2 = reshape(temp,S3,1);
% 计算隐含层神经元的输出
A1 = tansig(W1*P,B1);
% 计算输出层神经元的输出
A2 = purelin(W2*A1,B2);
% 计算均方误差
SE = mse(T-A2);
% 思维进化算法的得分
val = 1 / SE;
% 个体与得分合并
subpop(i,:) = [x val];
end
3.3种群成熟判别函数
ismature()函数为种群成熟判别函数,其调用格式为:
[flag,index]= ismature(pop)
其中, pop为待判别的子种群; flag为种群成熟标志:若flag =0,则子种群不成熟,若flag =1,则子种群成熟;index为子种群中得分最高的个体对应的索引号。
ismature.m函数文件的具体内容如下:
function [flag,index] = ismature(pop)
[~,index] = max(pop(:,end));
if index == 1
flag = 1;
else
flag = 0;
end3.4 主函数
主函数为main.m文件,具体如下:
%% 思维进化算法应用于优化BP神经网络的初始权值和阈值
%% 清空环境变量
clear all
clc
warning off
%% 导入数据
load data.mat
% 随机生成训练集、测试集
k = randperm(size(input,1));
N = 1900;
% 训练集——1900个样本
P_train=input(k(1:N),:)';
T_train=output(k(1:N));
% 测试集——100个样本
P_test=input(k(N+1:end),:)';
T_test=output(k(N+1:end));
%% 归一化
% 训练集
[Pn_train,inputps] = mapminmax(P_train);
Pn_test = mapminmax('apply',P_test,inputps);
% 测试集
[Tn_train,outputps] = mapminmax(T_train);
Tn_test = mapminmax('apply',T_test,outputps);
%% 参数设置
popsize = 200; % 种群大小
bestsize = 5; % 优胜子种群个数
tempsize = 5; % 临时子种群个数
SG = popsize / (bestsize+tempsize); % 子群体大小
S1 = size(Pn_train,1); % 输入层神经元个数
S2 = 5; % 隐含层神经元个数
S3 = size(Tn_train,1); % 输出层神经元个数
iter = 10; % 迭代次数
%% 随机产生初始种群
initpop = initpop_generate(popsize,S1,S2,S3,Pn_train,Tn_train);
%% 产生优胜子群体和临时子群体
% 得分排序
[sort_val,index_val] = sort(initpop(:,end),'descend');
% 产生优胜子种群和临时子种群的中心
bestcenter = initpop(index_val(1:bestsize),:);
tempcenter = initpop(index_val(bestsize+1:bestsize+tempsize),:);
% 产生优胜子种群
bestpop = cell(bestsize,1);
for i = 1:bestsize
center = bestcenter(i,:);
bestpop{i} = subpop_generate(center,SG,S1,S2,S3,Pn_train,Tn_train);
end
% 产生临时子种群
temppop = cell(tempsize,1);
for i = 1:tempsize
center = tempcenter(i,:);
temppop{i} = subpop_generate(center,SG,S1,S2,S3,Pn_train,Tn_train);
end
while iter > 0
%% 优胜子群体趋同操作并计算各子群体得分
best_score = zeros(1,bestsize);
best_mature = cell(bestsize,1);
for i = 1:bestsize
best_mature{i} = bestpop{i}(1,:);
best_flag = 0; % 优胜子群体成熟标志(1表示成熟,0表示未成熟)
while best_flag == 0
% 判断优胜子群体是否成熟
[best_flag,best_index] = ismature(bestpop{i});
% 若优胜子群体尚未成熟,则以新的中心产生子种群
if best_flag == 0
best_newcenter = bestpop{i}(best_index,:);
best_mature{i} = [best_mature{i};best_newcenter];
bestpop{i} = subpop_generate(best_newcenter,SG,S1,S2,S3,Pn_train,Tn_train);
end
end
% 计算成熟优胜子群体的得分
best_score(i) = max(bestpop{i}(:,end));
end
% 绘图(优胜子群体趋同过程)
figure
temp_x = 1:length(best_mature{1}(:,end))+5;
temp_y = [best_mature{1}(:,end);repmat(best_mature{1}(end),5,1)];
plot(temp_x,temp_y,'b-o')
hold on
temp_x = 1:length(best_mature{2}(:,end))+5;
temp_y = [best_mature{2}(:,end);repmat(best_mature{2}(end),5,1)];
plot(temp_x,temp_y,'r-^')
hold on
temp_x = 1:length(best_mature{3}(:,end))+5;
temp_y = [best_mature{3}(:,end);repmat(best_mature{3}(end),5,1)];
plot(temp_x,temp_y,'k-s')
hold on
temp_x = 1:length(best_mature{4}(:,end))+5;
temp_y = [best_mature{4}(:,end);repmat(best_mature{4}(end),5,1)];
plot(temp_x,temp_y,'g-d')
hold on
temp_x = 1:length(best_mature{5}(:,end))+5;
temp_y = [best_mature{5}(:,end);repmat(best_mature{5}(end),5,1)];
plot(temp_x,temp_y,'m-*')
legend('子种群1','子种群2','子种群3','子种群4','子种群5')
xlim([1 10])
xlabel('趋同次数')
ylabel('得分')
title('优胜子种群趋同过程')
%% 临时子群体趋同操作并计算各子群体得分
temp_score = zeros(1,tempsize);
temp_mature = cell(tempsize,1);
for i = 1:tempsize
temp_mature{i} = temppop{i}(1,:);
temp_flag = 0; % 临时子群体成熟标志(1表示成熟,0表示未成熟)
while temp_flag == 0
% 判断临时子群体是否成熟
[temp_flag,temp_index] = ismature(temppop{i});
% 若临时子群体尚未成熟,则以新的中心产生子种群
if temp_flag == 0
temp_newcenter = temppop{i}(temp_index,:);
temp_mature{i} = [temp_mature{i};temp_newcenter];
temppop{i} = subpop_generate(temp_newcenter,SG,S1,S2,S3,Pn_train,Tn_train);
end
end
% 计算成熟临时子群体的得分
temp_score(i) = max(temppop{i}(:,end));
end
% 绘图(临时子群体趋同过程)
figure
temp_x = 1:length(temp_mature{1}(:,end))+5;
temp_y = [temp_mature{1}(:,end);repmat(temp_mature{1}(end),5,1)];
plot(temp_x,temp_y,'b-o')
hold on
temp_x = 1:length(temp_mature{2}(:,end))+5;
temp_y = [temp_mature{2}(:,end);repmat(temp_mature{2}(end),5,1)];
plot(temp_x,temp_y,'r-^')
hold on
temp_x = 1:length(temp_mature{3}(:,end))+5;
temp_y = [temp_mature{3}(:,end);repmat(temp_mature{3}(end),5,1)];
plot(temp_x,temp_y,'k-s')
hold on
temp_x = 1:length(temp_mature{4}(:,end))+5;
temp_y = [temp_mature{4}(:,end);repmat(temp_mature{4}(end),5,1)];
plot(temp_x,temp_y,'g-d')
hold on
temp_x = 1:length(temp_mature{5}(:,end))+5;
temp_y = [temp_mature{5}(:,end);repmat(temp_mature{5}(end),5,1)];
plot(temp_x,temp_y,'m-*')
legend('子种群1','子种群2','子种群3','子种群4','子种群5')
xlim([1 10])
xlabel('趋同次数')
ylabel('得分')
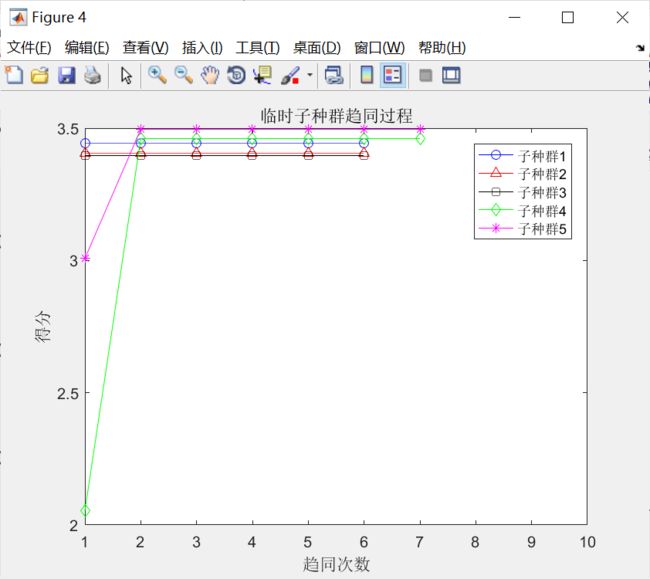
title('临时子种群趋同过程')
%% 异化操作
[score_all,index] = sort([best_score temp_score],'descend');
% 寻找临时子群体得分高于优胜子群体的编号
rep_temp = index(find(index(1:bestsize) > bestsize)) - bestsize;
% 寻找优胜子群体得分低于临时子群体的编号
rep_best = index(find(index(bestsize+1:end) < bestsize+1) + bestsize);
% 若满足替换条件
if ~isempty(rep_temp)
% 得分高的临时子群体替换优胜子群体
for i = 1:length(rep_best)
bestpop{rep_best(i)} = temppop{rep_temp(i)};
end
% 补充临时子群体,以保证临时子群体的个数不变
for i = 1:length(rep_temp)
temppop{rep_temp(i)} = initpop_generate(SG,S1,S2,S3,Pn_train,Tn_train);
end
else
break;
end
%% 输出当前迭代获得的最佳个体及其得分
if index(1) < 6
best_individual = bestpop{index(1)}(1,:);
else
best_individual = temppop{index(1) - 5}(1,:);
end
iter = iter - 1;
end
%% 解码最优个体
x = best_individual;
% 前S1*S2个编码为W1
temp = x(1:S1*S2);
W1 = reshape(temp,S2,S1);
% 接着的S2*S3个编码为W2
temp = x(S1*S2+1:S1*S2+S2*S3);
W2 = reshape(temp,S3,S2);
% 接着的S2个编码为B1
temp = x(S1*S2+S2*S3+1:S1*S2+S2*S3+S2);
B1 = reshape(temp,S2,1);
%接着的S3个编码B2
temp = x(S1*S2+S2*S3+S2+1:end-1);
B2 = reshape(temp,S3,1);
% E_optimized = zeros(1,100);
% for i = 1:100
%% 创建/训练BP神经网络
net_optimized = newff(Pn_train,Tn_train,S2);
% 设置训练参数
net_optimized.trainParam.epochs = 100;
net_optimized.trainParam.show = 10;
net_optimized.trainParam.goal = 1e-4;
net_optimized.trainParam.lr = 0.1;
% 设置网络初始权值和阈值
net_optimized.IW{1,1} = W1;
net_optimized.LW{2,1} = W2;
net_optimized.b{1} = B1;
net_optimized.b{2} = B2;
% 利用新的权值和阈值进行训练
net_optimized = train(net_optimized,Pn_train,Tn_train);
%% 仿真测试
Tn_sim_optimized = sim(net_optimized,Pn_test);
% 反归一化
T_sim_optimized = mapminmax('reverse',Tn_sim_optimized,outputps);
%% 结果对比
result_optimized = [T_test' T_sim_optimized'];
% 均方误差
E_optimized = mse(T_sim_optimized - T_test)
% end
%% 未优化的BP神经网络
% E = zeros(1,100);
% for i = 1:100
net = newff(Pn_train,Tn_train,S2);
% 设置训练参数
net.trainParam.epochs = 100;
net.trainParam.show = 10;
net.trainParam.goal = 1e-4;
net.trainParam.lr = 0.1;
% 利用新的权值和阈值进行训练
net = train(net,Pn_train,Tn_train);
%% 仿真测试
Tn_sim = sim(net,Pn_test);
% 反归一化
T_sim = mapminmax('reverse',Tn_sim,outputps);
%% 结果对比
result = [T_test' T_sim'];
% 均方误差
E = mse(T_sim - T_test)
% end
E_optimized =
0.0441
E =
0.0081
与上述过程对应的初始优胜子种群和临时子种群的趋同过程,如下图所示。分别观察,不难发现:
①经过若干次趋同操作,各个子种群均已成熟(得分不再增加);
②允许存在这样一些子种群,如优胜子种群中的子种群1,3,4和临时子种群中的子种群3,并没有执行趋同操作,因为在子种群中心周围,没有发现更好的个体。
③对比可以发现:待优胜子种群和临时子种群成熟后,临时在一些子种群,其得分比优胜子种群中的一些子种群得分高,譬如,临时子种群中的子种群1、2.5与优胜子种群中的子种群3、4、5,因此需要执行3次异化操作,同时需要补充3个新的子种群到临时子种群中。
5案例扩展
5.1得分函数的设计
得分函数,与遗传算法中的适应度函数概念一致,是评价个体性能的指标。本文选用的得分函数是训练集均方误差的倒数。为了方便读者学习,这里对得分函数的设计作简要讨论,当然,读者也可以自定义得分函数。
1)回归拟合问题
对于回归拟合问题,一般的评价指标涵盖均方误差、误差平方和,决定系数和相对误差等。
2)分类问题
对于分类问题,一般的评价指标涵盖整体正确率、正类正确率和负类正确率等
3)样本来源
从样本来源的角度来讲,一般有以下两个方案:
①利用训练集的样本进行指标计算;
②利用验证集的样本进行指标计算。
由于思维进化算法中的一些参数,比如种群规模、优胜子群体和临时子群体的个数,迭代进化停止条件等,对优化的结果均有影响,因此不少专家和学者在这方面做了许多卓有成效的研究,为思维进化算法的理论支撑及广泛应用奠定了扎实的基础。对此感兴趣的读者,可以深入学习参考文献中的相关论文。