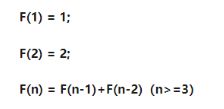leetcode：70. 爬楼梯

题目来源

leetcode

题目描述

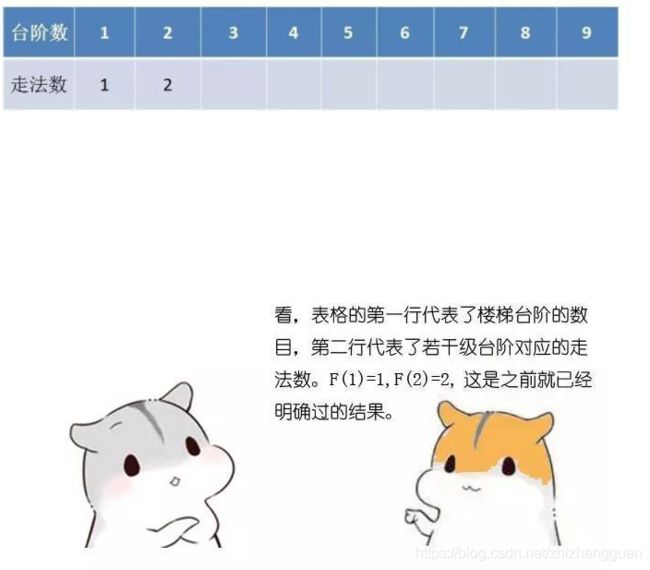
比如，每次走1级台阶，一共走10步，这是其中一种走法。我们可以简写成 1,1,1,1,1,1,1,1,1,1。

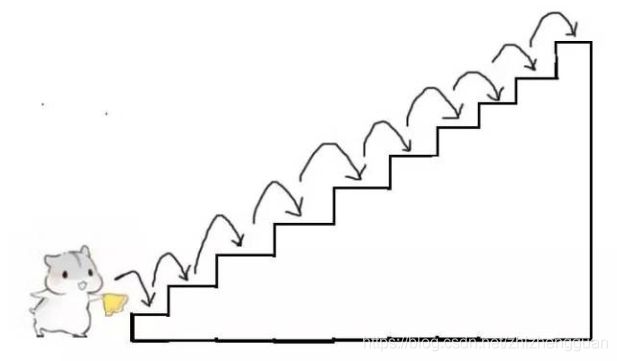
再比如，每次走2级台阶，一共走5步，这是另一种走法。我们可以简写成 2,2,2,2,2。

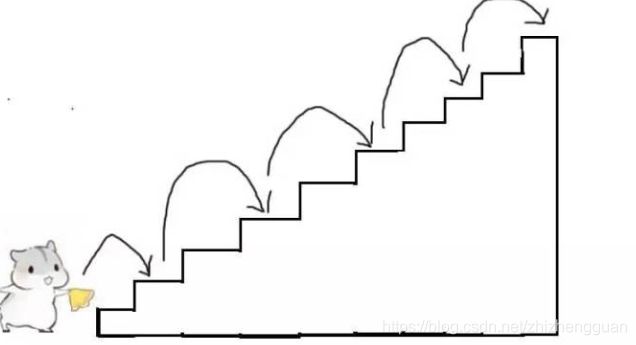
class Solution {
public:
    int climbStairs(int n) {

    }
};

题目解析

问题建模（从上到下）

第一个问题：我们站到最终点来看，如果我们只差最后一步就走到第10级台阶，这时候会出现几种情况呢？

• 当然是两种情况：因为每一步只允许走1级或者2级台阶。所以对于最后一步：
  • 第一种情况：从9级走到10级
  • 第二种情况：从8级走到10级
• 也就是说：想要走到第10级，最后必然是从8级或者第9级开始。

第一种情况：

第二种情况：

小结：

• 对于动态规划的题目，我们第一步要做的是从终点来看，只看最后一步，会是怎么到达终点的。
• 比如对于本题，我们要先忽略从0走到8级的过程，以及从0走到9级的过程。只看最后的状态可能会从哪里转移来的

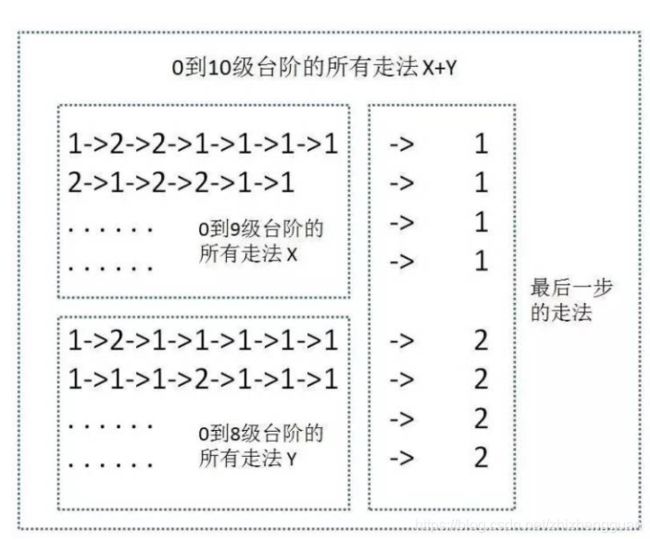
第二个问题：假设我们已经知道0到9级台阶的走法有X种，0到8级台阶的走法有Y中，那么0到10级台阶的走法有几种？

• 我们知道：
  • 想要走到第10级，最后必然是从8级或者第9级开始。
  • 现在8级的走法和9级的走法已经知道，要求求出10级的走法
  • 也就是说，要求 F(10)、F(9)、F(8)这三者的关系
• 思考：
  • 10级台阶的走法可以根基最后一步的不同而分成两部分。
  • 第1部分的最后一步是从9级到10级，这部分的走法数量和9级台阶的走法数量是相等的，也就是X
  • 第2部分的最后一步是从8级到10级，这部分的走法数量和8级台阶的走法数量是相等的，也就是Y
  • 这两部分相加，就是总的走法数量，也就是X + Y
  • 把思路画出来，就是这样子：
    
• 结论：
  • 从0到10级台阶的走法数量 = 0到9级台阶的走法数量 + 0 到8级台阶的走法数量
  • 即F(10) = F(9) + F(8)

小结：

• 还是从终点向下看 ，假设之前的子问题答案已经知道了。求当前原问题的答案与它的子问题的答案的关系

第三个问题：已经知道F(10) = F(9) + F(8)，那么如何求出F(9)和F(8)呢？

• 还是用刚才的思路，可以得出：
  • F(9) = F(8) + F(7);
  • F(8) = F(7) + F(6);
  • …
  • F(3) = F(1) + F(2)
    
• 当只有1级台阶和2级台阶的时候有几种解法呢？显然是1和2
• 由此，我们可以归纳出如下的公式：
  
  小结：从最后一步递推，看它和前面的状态是什么关系。

动态规划的三个重要概念：最优子结构、边界、状态转移方程

• 上面我们知道F(10) = F(9) + F(8)，因此F(9)和F(8)是F(10)的最优子结构
• 当只有1级台阶或2级台阶的时候，我们可以直接得出结果，无需继续简化。我们称F(1)或者F(2)是问题的【边界】。如果一个问题没有边界，将永远无法得到有限的结果
• F(n) = F(n - 1) + F(n - 2)是阶段与阶段之间的状态转移方程。这是动态规划的核心，决定了问题的每一个阶段与下一个阶段的关系

求解问题（从上到下）

递归求解

    public static int climbStairs(int n) {
        if (n < 1){
            return 0;
        }
        if (n == 1){
            return 1;
        }
        if (n == 2){
            return 2;
        }
        return climbStairs(n - 1) + climbStairs(n - 2);
    }

时间复杂度分析

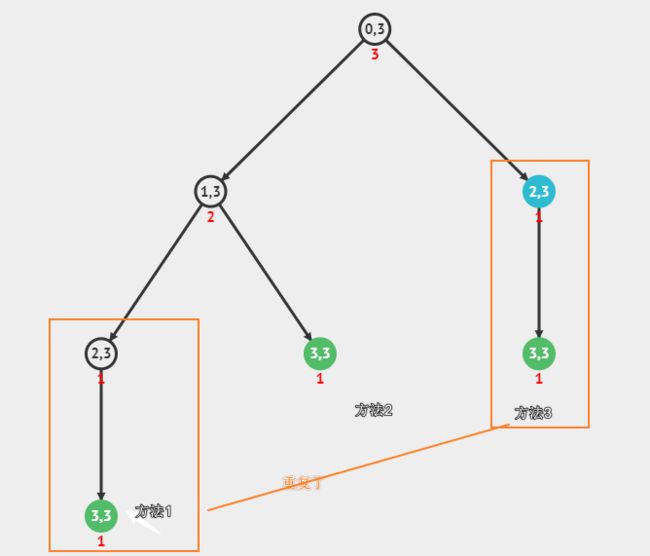
其实递归的时间复杂度计算并不难，我们先分析出递归方法所走过的路径：

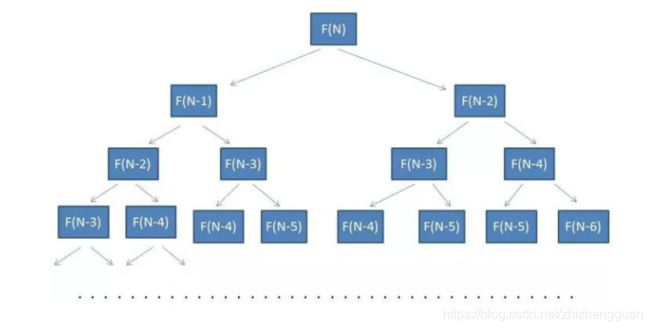
• 要计算出F(N)，就要先得到F(N - 1)和F(N - 2)的值，要计算F(N - 1)，就要先得到F(N - 2)和F(N - 3)的值…以此类推，可以归纳出下面的图：

• 可以看出，这其实是一颗二叉树。数的节点个数就是我们的递归方法需要计算的次数
• 不难看出，这颗二叉树的高度是N - 1，节点个数解决2的N-1次方。所以方法的时间复杂度可以近似的看成是O(2^N)

时间效率是指数级别的，太低了。

备忘录算法

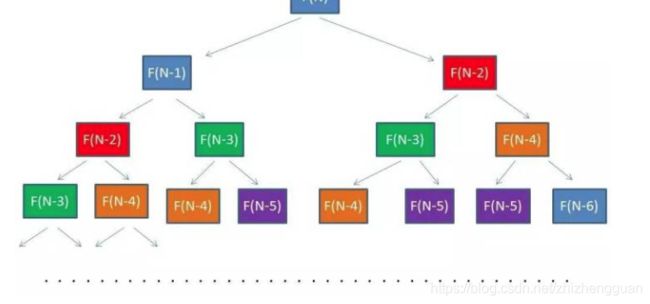
回顾下刚刚的递归图，我们可以发现有些相同的参数被重复计算了（如下图所示，相同的颜色代表了方法被传入相同的参数）

如果想要避免重复计算，我们可以用创建一个哈希表，每次把不同的参数的计算结果存入哈希。当遇到相同参数时，再从哈希表中取出，就不用重复计算了。这个算法有个专有名词，备忘录算法

class Solution {
    // 递归时由大量的重复运算，我们可以用一个map把原来算出来的值存起来以便以后使用
    static Map<Integer, Integer> maps =  new HashMap<Integer, Integer>();
    public int climbStairs(int n) {
        if (n < 1){
            return 0;
        }
        if (n == 1){
            return 1;
        }
        if (n == 2){
            return 2;
        }

		
        if (maps.containsKey(n)){  
            return maps.get(n);
        }else{
            int value = climbStairs(n - 1) + climbStairs(n - 2);
            maps.put(n, value);
            return value;
        }
    }
}

在以上代码中，集合map是一个备忘录。当每次需要计算F(N)的时候，会首先从map中寻找匹配元素。如果map中存在，就直接返回结果，如果map中不存在，就计算出结果，存入备忘录中。

时间复杂度和空间复杂度分析

• 从F(1)到F(N)一共有N个不同的输入，在哈希表中存了N-2个结果，所以时间复杂度和空间复杂度都是O(N)

思考：

• 想想看，我们一定要对F(N)自顶而下做递归运算呢？可不可以自底而上，用迭代的方法推导出结果呢？
• 这就是动态规划了

动态规划

动态规划五部曲：

1）确定dp数组以及下标的含义

• dp[i]：爬到第i层楼梯，有dp[i]种方法

2）确定递推公式

• 从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。
  • 首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。
  • 还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。
• 那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！即dp[i] = dp[i - 1] + dp[i - 2]
• 在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。
• 这体现出确定dp数组以及下标的含义的重要性！

3）dp数组如何初始化

• 回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]中方法
• 那么i为0，dp[i]应该是多少呢。
  • 一种解释是：强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1
  • 一种解释是：在第0层的时候，一步只能走一个台阶或者两个台阶，然而楼层是0，直接站楼顶上了，就是不用方法，dp[0]就应该是0.
• 那到底是多少呢？
• 需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。所以本题其实就不应该讨论dp[0]的初始化！
• 因此，结论是：不考虑dp[0]如果初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。

4）确定遍历顺序

• 从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的

5）举例推导dp数组

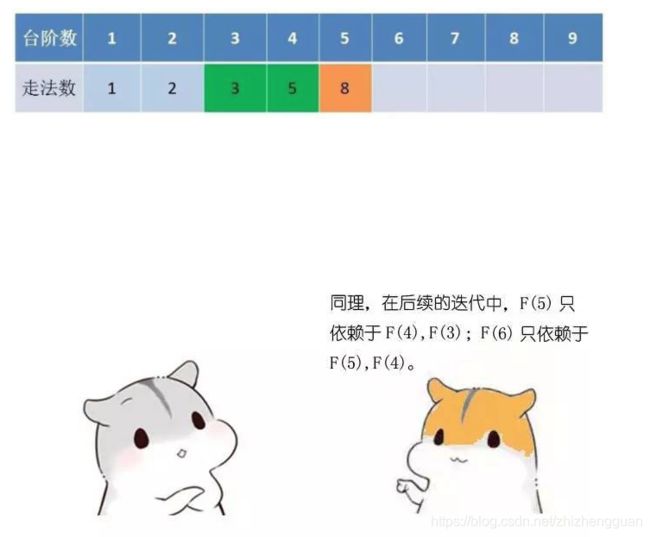
• 举例当n为5的时候，dp table（dp数组）应该是这样的
  
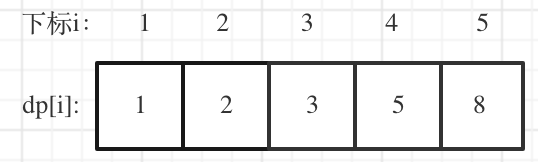
• 如果代码出问题了，就把dp table 打印出来，看看究竟是不是和自己推导的一样。
• 这不就是斐波那契数列么！唯一的区别是，没有讨论dp[0]应该是什么，因为dp[0]在本题没有意义！

以上五部分析完之后，C++代码如下：

// 版本一
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针
        vector<int> dp(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是从3开始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

当然依然也可以，优化一下空间复杂度，代码如下：

// 版本二
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(1)$

动态规划本质上是一个填表过程

这道爬楼梯的题目仅仅是动态规划中最简单的问题，因为它只有一个变化维度。还有很多问题远比这要复杂得多

思路二（从下到上）

暴力递归

定义一个签名，如下，表示为：从位置curr走到位置n一共有几种方法

int process(int curr, int n)

假设我们站在楼梯curr上

• 如果curr == N，那么说明已经走到了终点，也就是找到了一种方法，因此直接返回1
• 如果curr == N - 1，那么下一步只有一种走法，也就是只能走一步
• 否则，其他情况下有两种选择：走一步，或者走两步

class Solution {
    int process(int curr, int n){
        if(curr == n){
            return 1;
        }

        if(curr == n - 1){
            return process(curr + 1, n);
        }

        return process(curr + 1, n) + process(curr + 2, n);
    }
public:
    int climbStairs(int n) {
        if(n < 0){
            return -1;
        }
        return process(0, n);
    }
};

当然，上面方法肯定会超时，因此，我们将它改为动态规划

暴力规划改动态递归

（1）第一步：准备一张表。

• 问题是，这张表是一维的还是二维的，应该多大。我们可以通过分析递归函数的可变参数有几个，其变化范围多大来决定

 int process(int curr, int n)

• 上面，curr是变化的，其变化范围是0~n；n是不变的
• 因为只有一个可变参数，所以dp应该是一维数组；因为变化范围是0~n，所以数组长度为n+1。也就是：

 std::vector<int> dp(n + 1)

（2）确定返回值

• 怎么确定呢？通过看主函数是怎么调用递归函数的

 return process(0, n);

• 可以看出，可变参数初始为0，所以应该返回$dp[0]$

（3）填表

（3.1）先初始化表，也就是看base case

 		if(curr == n){
            return 1;
        }

• 因此初始化$dp[n]=1$

（3.2） 再分析普通情况，这个时候要分析清楚依赖关系

 		if(curr == n - 1){
            return process(curr + 1, n);
        }

        return process(curr + 1, n) + process(curr + 2, n);

• 由curr + 1和curr + 2可以看出，它依赖比它大的数，所以我们应该从大到小填写表格

		for (int curr = n - 1; curr >= 0; --curr) {
            
        }

• 至于里面怎么填，根据上面的直接抄写就行了

（4）综上

class Solution {
    int process(int curr, int n){
        if(curr == n){
            return 1;
        }

        if(curr == n - 1){
            return process(curr + 1, n);
        }

        return process(curr + 1, n) + process(curr + 2, n);
    }
public:
    int climbStairs(int n) {
        if(n < 0){
            return -1;
        }
        
        std::vector<int> dp(n + 1);
        dp[n] = 1;
        for (int curr = n - 1; curr >= 0; --curr) {
            if(curr == n - 1){
                dp[curr] = dp[curr + 1];
            }else{
                dp[curr] = dp[curr + 1] + dp[curr + 2];
            }
        }
        return dp[0];
    }
};

类似题目

题目	思路
leetcode：70. 爬楼梯 Climbing Stairs	动态规划
leetcode：746. 使用最小花费爬楼梯 Min Cost Climbing Stairs	动态规划
leetcode：509. 斐波那契数列 Fibonacci Number	动态规划
leetcode：91. 解码方法Decode Ways
leetcode：639. *可以匹配多个字符时，有多少解码方法 II Decode Ways II
leetcode：842. 将数组拆分成斐波那契序列，返回一个成功的组合 Split Array into Fibonacci Sequence	回溯
leetcode：306. 字符串是否能切割成斐波那契序列 Additive Number
leetcode：873. 最长的斐波那契序列长度 Length of Longest Fibonacci Subsequence
Coin Change