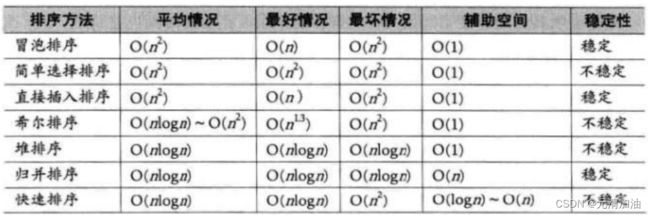
排序(七种排序)
1.插入排序
2.希尔排序
3.选择排序4.堆排序5.冒泡排序6.快速排序7.归并排序
1.插入排序
1.1思路
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列
1.2实现
//插入排序 void InsertSort(int* a, int n) { for (int i = 0; i < n - 1; ++i) { // [0, end] 有序,插入tmp依旧有序 int end = i; int tmp = a[i + 1]; while (end >= 0) { if (a[end] > tmp) { a[end + 1] = a[end]; --end; } else { break; } } a[end + 1] = tmp; } }
2. 希尔排序
2.1思路
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
2.2实现
void ShellSort(int* a, int n) { // 1、gap > 1 预排序 // 2、gap == 1 直接插入排序 int gap = n; while (gap > 1) { gap = gap / 3 + 1; // +1可以保证最后一次一定是1 // gap = gap / 2; for (int i = 0; i < n - gap; ++i) { int end = i; int tmp = a[end + gap]; while (end >= 0) { if (a[end] > tmp) { a[end + gap] = a[end]; end -= gap; } else { break; } } a[end + gap] = tmp; } } }
3. 选择排序
3.1思路
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
3.2实现
void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } void SelectSort(int* a, int n) { int begin = 0, end = n - 1; while (begin < end) { //找出最大和最小值放在开头和结尾,然后begin++,end-- int maxi = begin, mini = begin; for (int i = begin; i <= end; i++) { if (a[i] > a[maxi]) { maxi = i; } if (a[i] < a[mini]) { mini = i; } } Swap(&a[begin], &a[mini]); // 如果maxi和begin重叠,修正一下即可 //如果maxi和begin重叠,可能会重复交换 if (begin == maxi) { maxi = mini; } Swap(&a[end], &a[maxi]); ++begin; --end; } }
4.堆排序
4.1思路
堆排序 是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。不知道堆的可以参考: 数据结构:堆的实现_元清加油的博客-CSDN博客
4.2实现
//向下调整法 void AdjustDown(int* a, int n, int parent) { int child = parent * 2 + 1; while (child < n) { // 找出小的那个孩子 if (child + 1 < n && a[child + 1] > a[child]) { ++child; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } // 排升序 void HeapSort(int* a, int n) { // 建大堆 for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown(a, n, i); } //堆删除的思想 int end = n - 1; while (end > 0) { Swap(&a[0], &a[end]); AdjustDown(a, end, 0); --end; } }
5.冒泡排序
5.1思路
冒泡排序非常的简单,相邻二个数比较大小,然后交换即可
5.2实现
void BubbleSort(int* a, int n) { for (int j = 0; j < n; ++j) { bool exchange = false; for (int i = 1; i < n - j; i++) { if (a[i - 1] > a[i]) { int tmp = a[i]; a[i] = a[i - 1]; a[i - 1] = tmp; exchange = true; } } if (exchange == false) { break; } } }
6.快速排序
6.1霍尔快排法
6.1.1思路
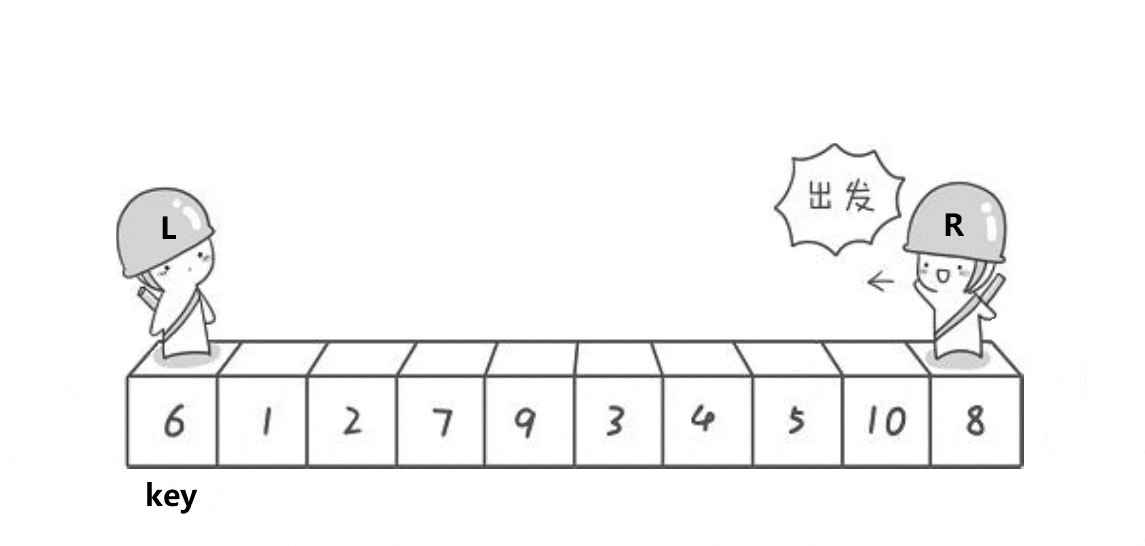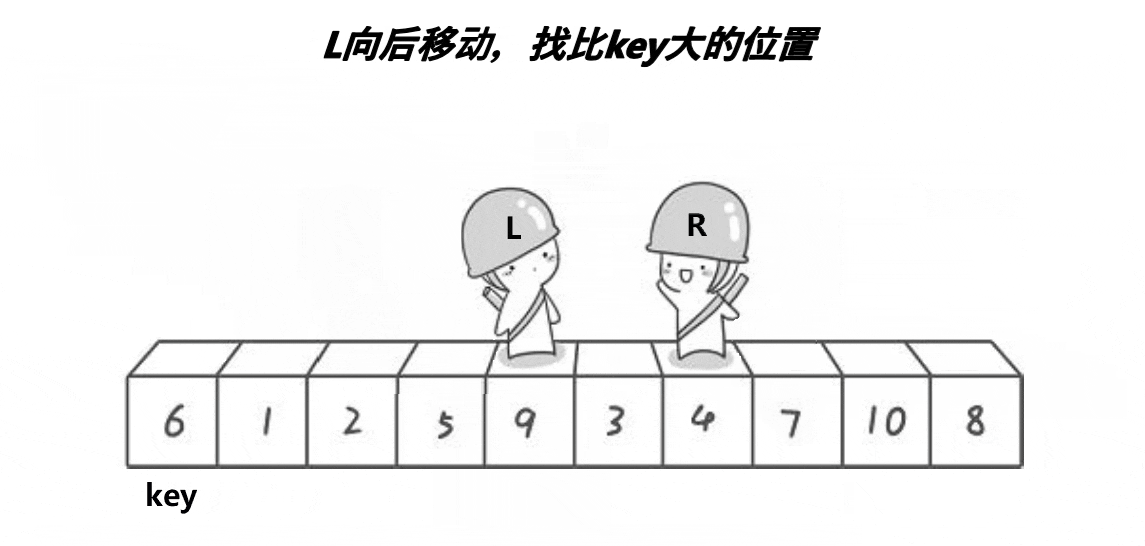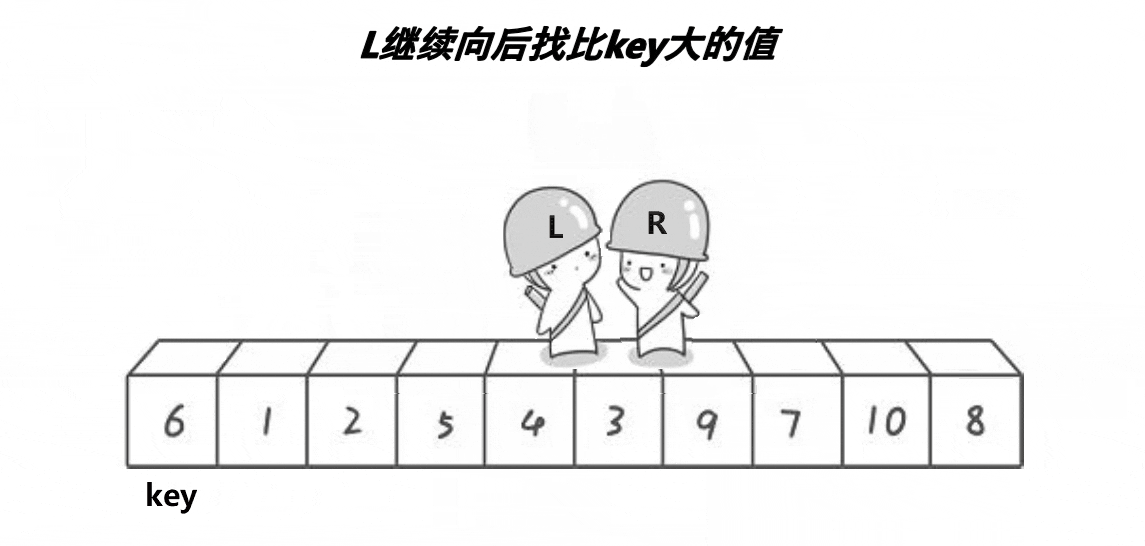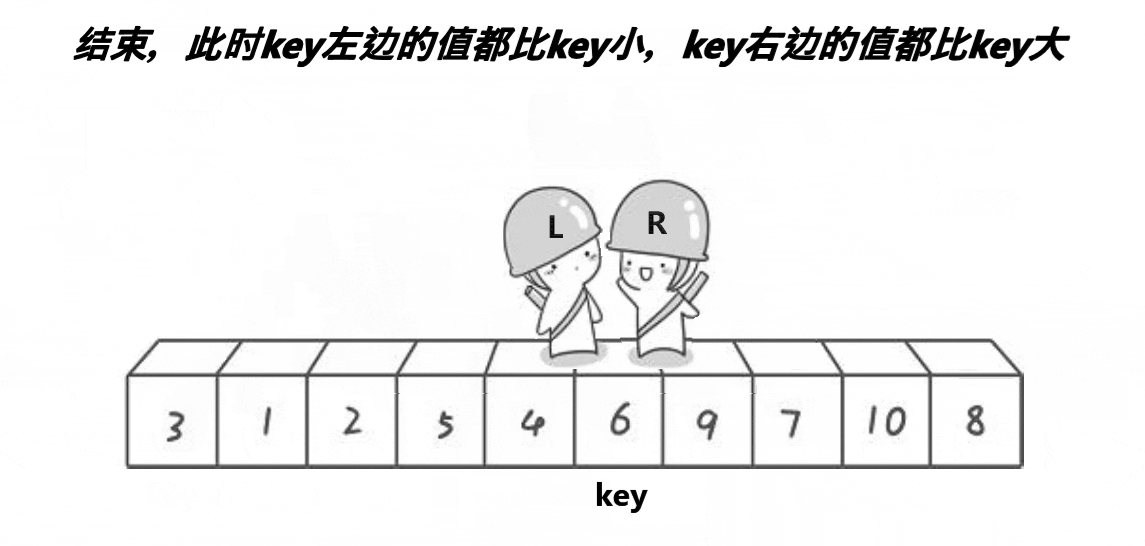
取第一个数为key,从左右出发,右边找小于key的数,左边找大于key的数,找到交换。直到左边大于右边,就交换key和左边的数
6.1.2 实现
void Swap(int* str1, int* str2) { int temp = *str1; *str1 = *str2; *str2 = temp; } int PartSort1(int* a, int left, int right) { int keyi = left; while (left < right) { // 右边找小 while (left < right && a[right] >= a[keyi]) { --right; } // 左边找大 while (left < right && a[left] <= a[keyi]) { ++left; } Swap(&a[left], &a[right]); } Swap(&a[keyi], &a[left]); return left; } void QuickSort(int* a, int begin, int end) { if (begin >= end) return; int keyi = PartSort2(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); } int main() { int arr[] = { 6,1,2,7,9,3,4,5,10,8 }; QuickSort(arr, 0, 9); for (int i = 0; i < 9; i++) { printf("%d ", arr[i]); } return 0; }
6.2挖坑法
6.2.1思路
取第一个数为key,从左右出发,右边找小于key的数,把他设立为一个坑位,左边找大于key的数,把他设立为一个新的坑位。直到左边大于右边,就交换key和坑的数
6.2.2实现
// 挖坑法 // [left, right] int PartSort2(int* a, int left, int right) { int key = a[left]; int hole = left; while (left < right) { // 右边找小 while (left < right && a[right] >= key) { --right; } a[hole] = a[right]; hole = right; // 左边找大 while (left < right && a[left] <= key) { ++left; } a[hole] = a[left]; hole = left; } a[hole] = key; return hole; } void QuickSort(int* a, int begin, int end) { if (begin >= end) return; int keyi = PartSort2(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); } int main() { int arr[] = { 6,1,2,7,9,3,4,5,10,8 }; QuickSort(arr, 0, 9); for (int i = 0; i < 9; i++) { printf("%d ", arr[i]); } return 0; }
6.3前后指针法
6.3.1思路
取第一个数为key,初始时,prev指针指向序列开头,cur指针指向prev后一个位置。cur找小与key的数与(prev++)交换
6.3.2实现
// 前后指针法 // [left, right] int PartSort3(int* a, int left, int right) { int prev = left; int cur = left + 1; int keyi = left; while (cur <= right) { if (a[cur] < a[keyi] && ++prev != cur) { Swap(&a[prev], &a[cur]); } ++cur; } Swap(&a[prev], &a[keyi]); keyi = prev; return keyi; } void QuickSort(int* a, int begin, int end) { if (begin >= end) return; int keyi = PartSort2(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); } int main() { int arr[] = { 6,1,2,7,9,3,4,5,10,8 }; QuickSort(arr, 0, 9); for (int i = 0; i < 9; i++) { printf("%d ", arr[i]); } return 0; }
7.归并排序
7.1思路
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用 分治法(Divide andConquer) 的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
7.2实现
//归并排序 void _MergeSort(int* a, int begin, int end, int* tmp) { if (begin == end) return; int mid = (begin + end) / 2; // [begin, mid] [mid+1, end] _MergeSort(a, begin, mid, tmp); _MergeSort(a, mid + 1, end, tmp); // 归并两个区间 // ... int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int i = begin; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] <= a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); _MergeSort(a, 0, n - 1, tmp); free(tmp); }