算法拾遗三十五indexTree和AC自动机
算法拾遗三十五indexTree和AC自动机
-
-
- indexTree(树状数组)
-
- indexTree规则
- IndexTree二维
- AC自动机
-
indexTree(树状数组)
给定数组下标统一从1开始
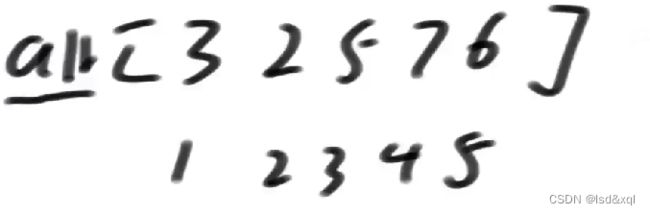
如果要求L。。R范围上任意区间的和,我们通常的解法是定义一个help(前缀和数组)数组,然后记录它的累加和
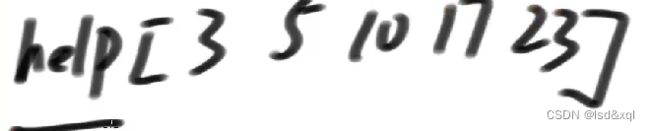
如果把arr中的某个数字改一下,则需要重新维护help数组。
如果我想同时支持arr中某个数字修改,也要快速查询出L。。R范围上的区间和,那么如上结构是不适用的。
indexTree不像线段树一样可以实现范围更新,indexTree适合单点更新查区间范围和的情况且时间复杂度相对于线段树更优
indexTree规则
有如下数组,下标从1开始:
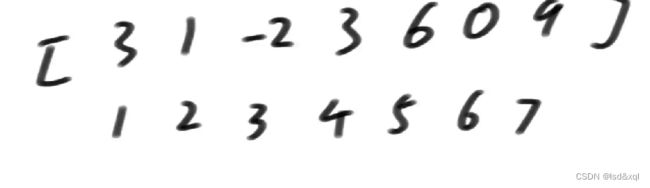
我想生成另一个help数组:
当前来到1位置,我前面没有和我长度为1的凑一对,所以help的1位置填入3,当来到2位置的时候,前面有和我长度为1的凑一对,2位置填入4。当来到3位置的时候,前面没有单独和我长度为1的凑一对,3位置填入-2,4位置前面有和我长度为1的凑一对,然后再往前看前面有没有长度为2的和我凑一对,发现有的所以4位置填5,然后依次类推下去。

上图中规律:
如果index=8,它应该管1-8范围的累加和,
8的二进制位01000,它管的范围为将二进制中最后一个1拆散之后再加1的第一个数到自己
00001-01000(就是1-8)
再来一个例子当index=12的时候,应该管9-12范围的和 12的二进制为01100,则管的范围可以化简为01001-01100【9-12】
已知了如上规律,有help数组之后,那么如何利用help数组求前缀和,如果要求33位置的前缀和,
则就只需要求0100001+0100000【抹掉最后一个1的位置】,一直抹完所有最后一个1的位置。

比如:
help【0110100】,原始arr中想要累加到它
help[0110100] = arr[0110001-0110100]
第二步
help[0110000]=arr[0100001-0110000]
分段求得的解的和就是0110100区间范围的累加和。
时间复杂度是logN水平,因为动的是位数
public class IndexTree {
// 下标从1开始!
public static class IndexTree {
private int[] tree;
private int N;
// 0位置弃而不用!
public IndexTree(int size) {
N = size;
tree = new int[N + 1];
}
// 1~index 累加和是多少?
public int sum(int index) {
int ret = 0;
while (index > 0) {
ret += tree[index];
index -= index & -index;
}
return ret;
}
// index & -index : 提取出index最右侧的1出来
// index : 0011001000
// index & -index : 0000001000
// -index = index取反加1
public void add(int index, int d) {
//如果要把index位置增加一个d
while (index <= N) {
tree[index] += d;
//index变化是当前index加上最右侧的1组成的数
index += index & -index;
}
}
//求影响的时候则由最右侧的1怼上去,累加就由最右侧的一减下来
}
public static class Right {
private int[] nums;
private int N;
public Right(int size) {
N = size + 1;
nums = new int[N + 1];
}
public int sum(int index) {
int ret = 0;
for (int i = 1; i <= index; i++) {
ret += nums[i];
}
return ret;
}
public void add(int index, int d) {
nums[index] += d;
}
}
public static void main(String[] args) {
int N = 100;
int V = 100;
int testTime = 2000000;
IndexTree tree = new IndexTree(N);
Right test = new Right(N);
System.out.println("test begin");
for (int i = 0; i < testTime; i++) {
int index = (int) (Math.random() * N) + 1;
if (Math.random() <= 0.5) {
int add = (int) (Math.random() * V);
tree.add(index, add);
test.add(index, add);
} else {
if (tree.sum(index) != test.sum(index)) {
System.out.println("Oops!");
}
}
}
System.out.println("test finish");
}
}
IndexTree二维
二维数组从(1,1)位置到(i,j)位置的整块累加和填入help(i,j)的格子里面
假设原数组图中?位置的值被改变了,那么help数组变化范围?
行管的是0110001-0110100
列管的是0110001-0111000
行列管的范围内所有组合都受影响

// 测试链接:https://leetcode.com/problems/range-sum-query-2d-mutable
// 但这个题是付费题目
// 提交时把类名、构造函数名从Code02_IndexTree2D改成NumMatrix
public class IndexTree2D {
private int[][] tree;
private int[][] nums;
private int N;
private int M;
public IndexTree2D(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) {
return;
}
N = matrix.length;
M = matrix[0].length;
tree = new int[N + 1][M + 1];
nums = new int[N][M];
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
update(i, j, matrix[i][j]);
}
}
}
private int sum(int row, int col) {
int sum = 0;
for (int i = row + 1; i > 0; i -= i & (-i)) {
for (int j = col + 1; j > 0; j -= j & (-j)) {
sum += tree[i][j];
}
}
return sum;
}
public void update(int row, int col, int val) {
if (N == 0 || M == 0) {
return;
}
int add = val - nums[row][col];
nums[row][col] = val;
for (int i = row + 1; i <= N; i += i & (-i)) {
for (int j = col + 1; j <= M; j += j & (-j)) {
tree[i][j] += add;
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
if (N == 0 || M == 0) {
return 0;
}
return sum(row2, col2) + sum(row1 - 1, col1 - 1) - sum(row1 - 1, col2) - sum(row2, col1 - 1);
}
}
AC自动机
(实质)前缀树+KMP
理解:假设有一个字典里面放着若干个敏感词,然后有一个大文章,AC自动机就是将大文章包含的每一个敏感词都收集到不能漏掉,并且将大文章包含了哪些敏感词都告诉我。
我们先将注意力放在敏感词上(“abc”,“bkf”,“abcd”),首先将敏感词的前缀树建立出来:

然后再对前缀树做升级,给前缀树做fail指针(做宽度优先遍历):
头节点的fail指针指向null,头节点的下一层的所有节点的fail指针指向头节点
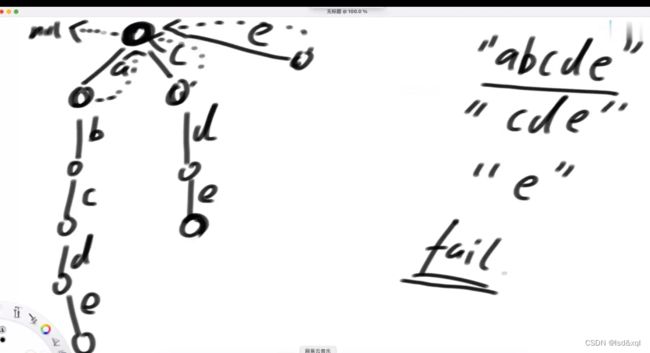
假设b路径下面的节点为x节点,则需要找x的父节点的fail指针指向的节点(这里是头节点)有没有直接指向b方向的路【此处没有】再找头节点的fail指针看有没有指向b方向的路,发现也没有,则让x节点的fail指针指向头节点,一直宽度优先遍历找下去得到:
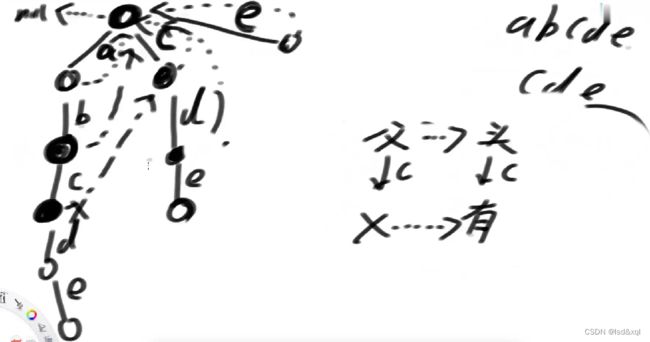
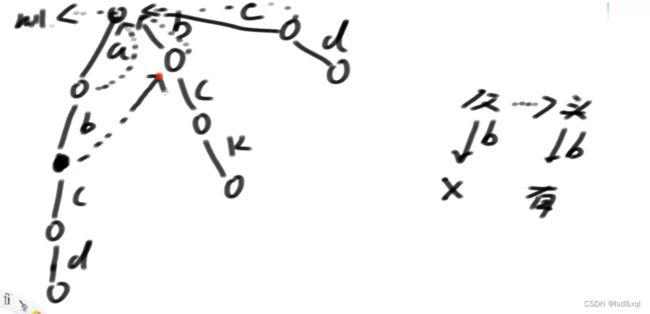
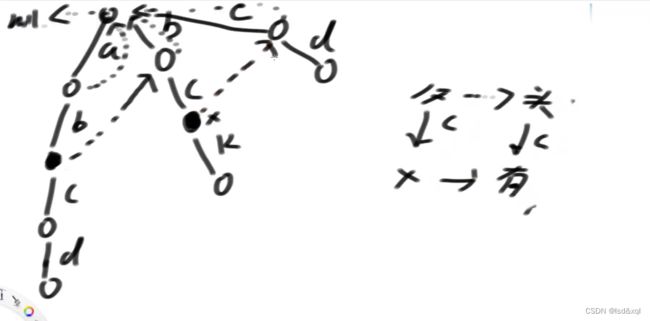
总结:
1、头节点的fail指针指向null
2、头节点的子节点的fail指针都指向头节点
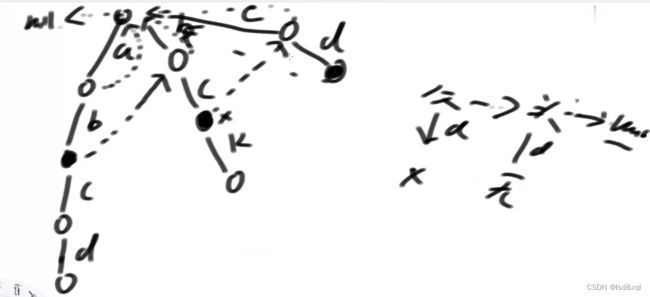
3、如果对于某个节点x它的父节点通过路径@指向x,然后父亲节点的fail指针为某个节点甲,如果甲有路径@则x的fail指针直接指向过去。
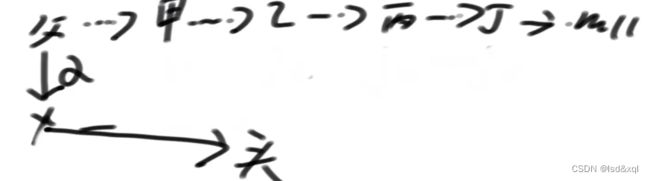
fail指针含义:
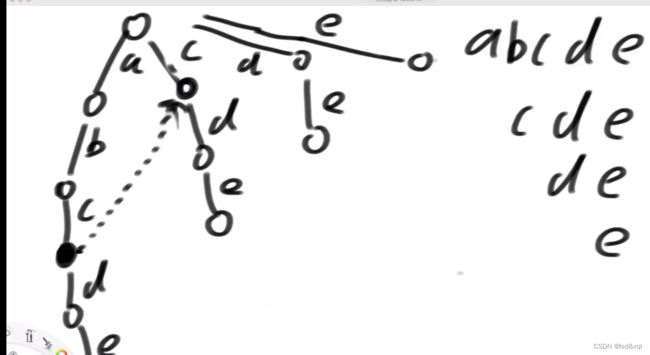
有如上图敏感词信息,首先知道c路径下的一个x节点的fail指针是指向【cde】路径下c下的y节点,x节点从上到下匹配到敏感词abcde中的abc,但是在匹配d的时候失败了,下面所有字符串中哪一个字符串的前缀,它一定跟我必须以c结尾的后缀的一样,且是最长的,如下图abcd中d的fail指针是指向cde中的d节点,它没有去找de而是找的cde。

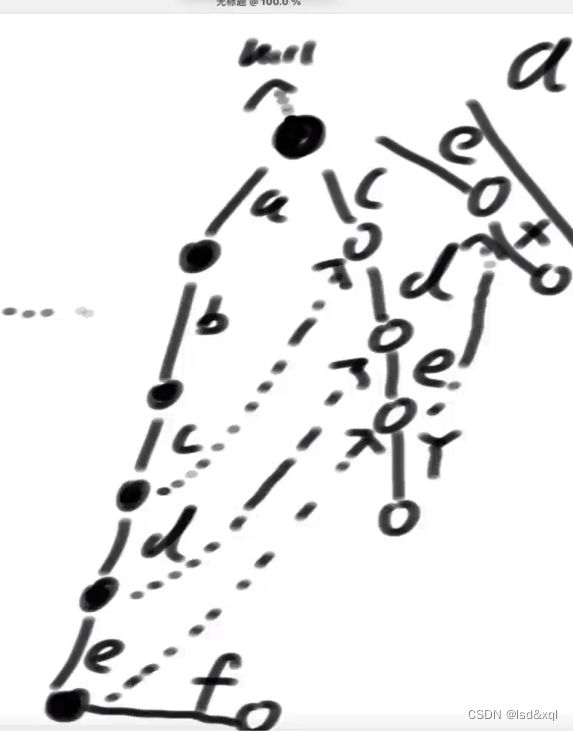
如上图没画虚线的fail指针都指向头节点,匹配大文章的过程中匹配到e位置后则匹配不上了,则需要通过e的fail指针来到必须以e结尾最长的前缀保留(cde),我准确的跳到有可能配到敏感词的下一个最可能的最近的位置,保证自己淘汰每一步都如此的小心,跳到第二个e位置,发现仍然匹配不上,然后再跳到第三个e位置。
第一层节点fail指针为什么指向头节点:
是因为如果a匹配到f的时候没找到任何节点可以匹配了,则可以通过fail指针跳到头节点重新找路径【相当于a不要了直接从f开始重新找】

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class AC {
// 前缀树的节点
public static class Node {
// 如果一个node,end为空,不是结尾
// 如果end不为空,表示这个点是某个字符串的结尾,end的值就是这个字符串
public String end;
// 只有在上面的end变量不为空的时候,endUse才有意义
// 表示,这个字符串之前有没有加入过答案
public boolean endUse;
public Node fail;
//前缀树都是字母表示
public Node[] nexts;
public Node() {
endUse = false;
end = null;
fail = null;
nexts = new Node[26];
}
}
public static class ACAutomation {
private Node root;
//新建头节点
public ACAutomation() {
root = new Node();
}
//前缀树加字符串
public void insert(String s) {
char[] str = s.toCharArray();
Node cur = root;
int index = 0;
for (int i = 0; i < str.length; i++) {
index = str[i] - 'a';
if (cur.nexts[index] == null) {
cur.nexts[index] = new Node();
}
cur = cur.nexts[index];
}
cur.end = s;
}
//build方法连fail指针
public void build() {
//准备队列做宽度优先遍历
Queue<Node> queue = new LinkedList<>();
//将头节点加入队列
queue.add(root);
Node cur = null;
Node cfail = null;
//由父来设置所有子的fail指针,当父弹出时设置关联子的fail指针
while (!queue.isEmpty()) {
// 某个父亲,cur
cur = queue.poll();
//考察所有的路(所有儿子节点)
for (int i = 0; i < 26; i++) { // 所有的路
// cur -> 父亲 如果有i号儿子,必须把i号儿子的fail指针设置好!
if (cur.nexts[i] != null) { // 如果真的有i号儿子
//先将孩子的fail指针设置成root
cur.nexts[i].fail = root;
//父亲的fail指针指向cfail,第一步跳转
cfail = cur.fail;
//如果父亲的fail指针不为null
while (cfail != null) {
//如果父亲的fail指针不为空,且有i方向的儿子
if (cfail.nexts[i] != null) {
//则让当前节点的儿子的fail指针指过去
cur.nexts[i].fail = cfail.nexts[i];
break;
}
//如果没有i方向的儿子则再往fail指针方向挑
cfail = cfail.fail;
}
queue.add(cur.nexts[i]);
}
}
}
}
// 大文章:content,在遍历每个单词的时候都顺着fail指针走一遍看是否有end串,有则收集
public List<String> containWords(String content) {
char[] str = content.toCharArray();
Node cur = root;
Node follow = null;
int index = 0;
List<String> ans = new ArrayList<>();
for (int i = 0; i < str.length; i++) {
index = str[i] - 'a'; // 当前路
// 如果当前字符在这条路上没配出来,就随着fail方向走向下条路径
while (cur.nexts[index] == null && cur != root) {
cur = cur.fail;
}
// 1) 现在来到的路径,是可以继续匹配的【来到的路正是我匹配期待的路,则继续往下走】
// 2) 现在来到的节点,就是前缀树的根节点
cur = cur.nexts[index] != null ? cur.nexts[index] : root;
//注意此处cur是没动的,而是通过follow去捞取的数据
follow = cur;
//来到任何节点过一圈fail指针
while (follow != root) {
//沿途一直蹦
if (follow.endUse) {
//之前的敏感词已经记录过了
break;
}
// 不同的需求,在这一段之间修改
if (follow.end != null) {
ans.add(follow.end);
//标记使用了这个字符串
follow.endUse = true;
}
// 不同的需求,在这一段之间修改
follow = follow.fail;
}
}
return ans;
}
}
public static void main(String[] args) {
ACAutomation ac = new ACAutomation();
ac.insert("dhe");
ac.insert("he");
ac.insert("abcdheks");
// 设置fail指针
ac.build();
List<String> contains = ac.containWords("abcdhekskdjfafhasldkflskdjhwqaeruv");
for (String word : contains) {
System.out.println(word);
}
}
}
首先大文章的长度是N,所有匹配串长度M
大文章一定会过一遍,时间复杂度O(N)。
所有匹配串被用来做了AC自动机,一个节点最多一条fail指针,并且根据代码来看:
while (follow != root) {
if (follow.end == -1) {
break;
}
{ // 不同的需求,在这一段{ }之间修改
ans += follow.end;
follow.end = -1;
} // 不同的需求,在这一段{ }之间修改
follow = follow.fail;
}
每一条fail指针最多走一遍,因为沿途的follow.end都会被设置为-1。
一旦被设置成-1,那么这条fail指针的链就不会继续跳转了。
ac自动机节点数:M
fail指针总数目:M
如果在ac自动机上往下走的代价被算进了遍历大文章的过程里。
所以时间复杂度O(N+M)。
“
如果想统计各匹配串的匹配次数,是不是不设置endUse来做次数累加。
如果是的话对均摊、最坏时间复杂度有没有影响。
如果统计匹配串匹配次数的话有没有AC自动机之外别的方法呢?
”
如果统计各匹配串的匹配次数,那么就不能让沿途的follow.endUse被设置为true。
因为一旦标记true,那么该匹配串就被命中过了,那么下次这个字符串可能就不会随着fail指针转圈被再次统计到了。
但是如果不让沿途的follow.endUse被设置为true,那么复杂度会因此升高的,不再是O(N+M),而是O(N*fail指针圈的平均长度)
“如果统计匹配串匹配次数的话有没有AC自动机之外别的方法呢?”
你可以继续用ac自动机。因为fail指针圈的平均长度,一般情况除非刻意构造,否则不会太长。
或者,你先用ac自动机,看看哪些串被匹配到了,但是不统计次数。
然后每一个串,开一个线程去跑kmp算法,单独统计这个串被大文章引用了多少次。利用多线程来搞。
但是用ac自动机,效率也不会低到哪去的。除非你刻意构造fail指针圈很长的例子。
