搜索二叉树
目录
一、什么叫搜索二叉树
二、搜索二叉树的操作
1、Insert(插入)
2、Find(查找)
3、InOrder(中序遍历)
4、Erase(删除)
三、搜索二叉树的应用
1、key模型
2、key/value模型
四,搜索二叉树模拟实现
一、什么叫搜索二叉树
搜索二叉树又称二叉排序树或二叉查找树,若不为空,则有以下性质
搜索二叉树有下面三条性质:
1、若它的左子树不为空,则左子树上所有结点的值都小于根结点的值
2、若它的右子树不为空,则右子树上所有结点的值都大于根结点的值
3、它的左右子树也分别为二叉搜索树
上图就是典型的搜索二叉树,根节点6,它的左子树上所有值都小于它,右子树所有值都大于它,并且左右字树也各自符合这个性质
如果想找一个数,最多查找高度次就可以找到
二、搜索二叉树的操作
下面的模拟实现中,代码有详细注释如何实现的
还有递归实现,都在下面的模拟实现的代码中
1、Insert(插入)
先和根结点相比,大于根结点再与根结点的右子树比,小于则跟左子树比,以此类推插入到合适的地方
2、Find(查找)
先和根结点相比,判断大小后再与左或右子树比,直到找到或未找到结束
3、InOrder(中序遍历)
递归调用,先左子树,再根结点,再右子树
4、Erase(删除)
①删除结点是叶子结点,例如图中的结点3
这里的情况①可以和情况②合并,不论删除结点是叶子结点还是有一个孩子,都可以将删除结点的父结点指向删除结点的子节点,情况①即指向空
所以就不需要判断删除结点是否是叶子结点了,代码更简洁些
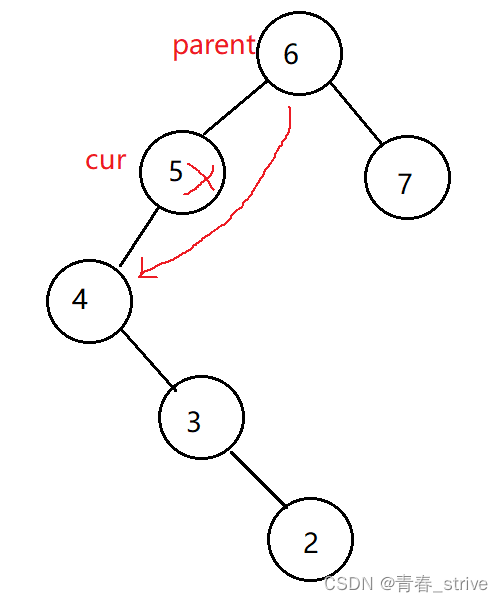
②删除结点只有一个孩子,例如图中的结点2,可以删除结点2后,将结点4直接指向被删除结点的那个子结点,即删除结点的左为空父亲指向它的右孩子,右为空父亲指向它的左孩子
这里还会有两种在父结点左还是右的情况:
第一种:
要删除cur结点,cur结点在parent结点的左,且cur结点的右为空,则parent的左指针指向结点4
第二种:
要删除cur结点,cur结点在parent结点的右,且cur结点的右为空,则parent的右指针指向结点2
这两种情况说明,在删除结点只有一个孩子的情况下,代码首先需要判断该删除结点在他它父结点的左边还是右边,不同的情况处理不同
最后还有一种特殊情况也要考虑到:删除的是root结点,这时的parent就不能访问了,直接改变root即可
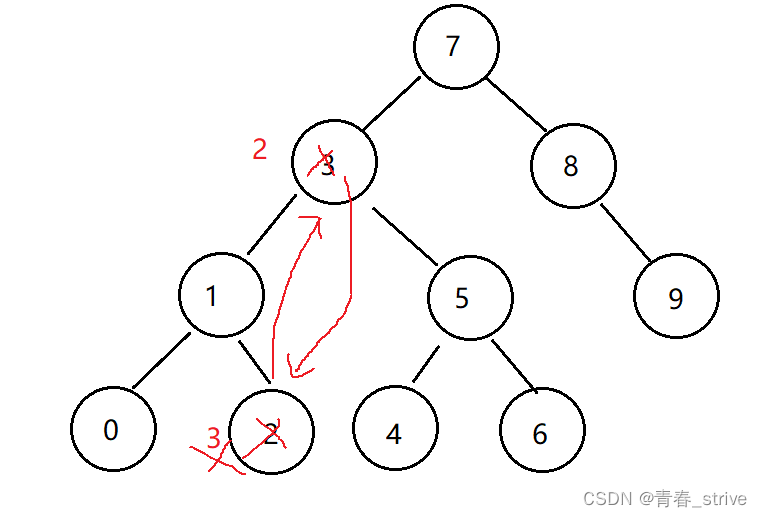
③若删除结点有两个孩子,则用替换法删除,比如需要删除结点3
删除结点是有两个孩子的,这时我们就需要用到替换法进行删除
替换方法是:替换删除结点的左子树的最大结点,或右子树最小的结点与该结点交换,然后删除替换结点
选择左子树的最大结点替换理由:删除结点的左子树本身都小于该结点,因此将左子树最大结点替换后,除去替换结点,它的左子树依旧小于该结点,也小于右子树的所有结点;并且作为左子树的最大结点也说明了该结点在左子树的最右边(搜索二叉树中右边始终大于左边),所以该结点要么没有孩子,要么只有一个孩子,符合了上面的①②条件,可以解决;以此类推,右子树最小的结点与该结点交换也成立
即如下图所示,若要删除结点3:
结点2作为结点3:左子树的最大结点,与结点3交换,然后删除结点3,变为下图:
删除结点后仍满足搜索二叉树的性质
三、搜索二叉树的应用
1、key模型
①小区的门禁卡
每个人都有对应的key绑定,进出的时候,会在类似二叉搜索树的模型中找,匹配了就开门
②查看文章中的单词是否出错
词库中的单词都插入到一个搜索树中,每个单词与词库中的单词比对,从而完成需求
2、key/value模型
①简单的中英翻译程序
即在实现搜索二叉树时,模版中加一个class V,表示每个结点都存一个英文一个中文,除了原来的成员,再加一个V _value,插入时也插入V,之后在查找的时候查找原来的key,找到了就输出与之相关的value
②高铁站等车站,买完票刷身份证即可
买完票,你的身份证就会和这个票绑定起来,你刷身份证的时候,就会检测是否买票,是否是当前日期,当前的车次
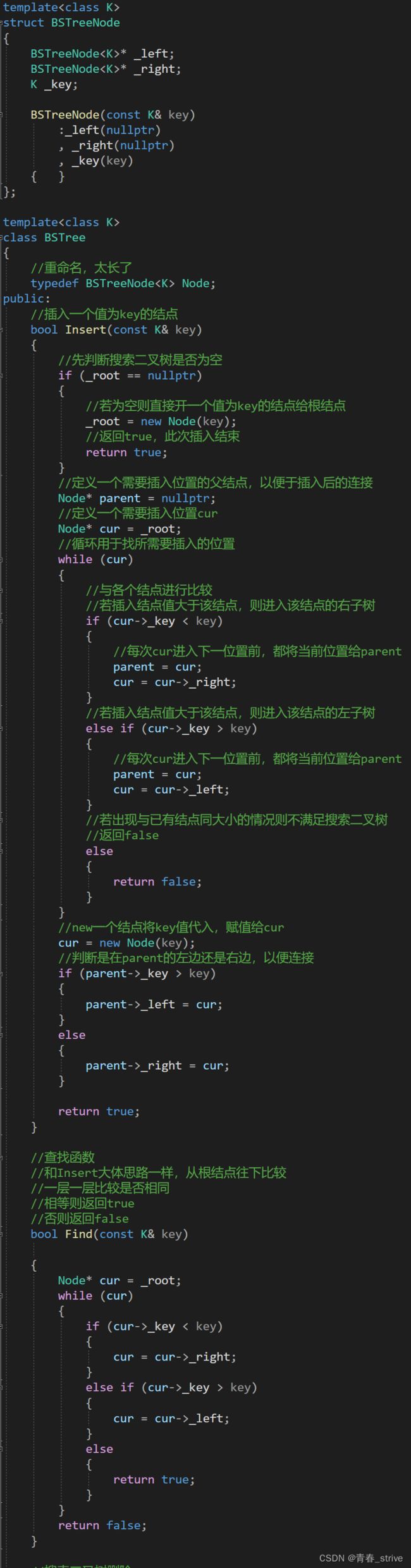
四,搜索二叉树模拟实现
里面有详细注释帮助理解底层原理
templatestruct BSTreeNode { BSTreeNode * _left; BSTreeNode * _right; K _key; BSTreeNode(const K& key) :_left(nullptr) , _right(nullptr) , _key(key) { } }; template class BSTree { //重命名,太长了 typedef BSTreeNode Node; public: //插入一个值为key的结点 bool Insert(const K& key) { //先判断搜索二叉树是否为空 if (_root == nullptr) { //若为空则直接开一个值为key的结点给根结点 _root = new Node(key); //返回true,此次插入结束 return true; } //定义一个需要插入位置的父结点,以便于插入后的连接 Node* parent = nullptr; //定义一个需要插入位置cur Node* cur = _root; //循环用于找所需要插入的位置 while (cur) { //与各个结点进行比较 //若插入结点值大于该结点,则进入该结点的右子树 if (cur->_key < key) { //每次cur进入下一位置前,都将当前位置给parent parent = cur; cur = cur->_right; } //若插入结点值大于该结点,则进入该结点的左子树 else if (cur->_key > key) { //每次cur进入下一位置前,都将当前位置给parent parent = cur; cur = cur->_left; } //若出现与已有结点同大小的情况则不满足搜索二叉树 //返回false else { return false; } } //new一个结点将key值代入,赋值给cur cur = new Node(key); //判断是在parent的左边还是右边,以便连接 if (parent->_key > key) { parent->_left = cur; } else { parent->_right = cur; } return true; } //查找函数 //和Insert大体思路一样,从根结点往下比较 //一层一层比较是否相同 //相等则返回true //否则返回false bool Find(const K& key) { Node* cur = _root; while (cur) { if (cur->_key < key) { cur = cur->_right; } else if (cur->_key > key) { cur = cur->_left; } else { return true; } } return false; } //搜索二叉树删除 bool Erase(const K& key) { Node* parent = nullptr; Node* cur = _root; //while循环在二叉树中找删除结点 while (cur) { if (cur->_key < key) { parent = cur; cur = cur->_right; } else if (cur->_key > key) { parent = cur; cur = cur->_left; } else { //找到待删除结点,开始删除 //删除结点的左为空 if (cur->_left == nullptr) { //判断删除的是否是根结点 if (cur == _root) { _root = cur->_right; } else { //判断删除结点在父结点的左还是右 if (cur == parent->_left) { parent->_left = cur->_right; } else { parent->_right = cur->_right; } } //删除结点并置空 delete cur; cur = nullptr; } //删除结点的右为空 else if (cur->_right == nullptr) { //判断删除的是否是根结点 if (cur == _root) { _root = cur->_left; } else { //判断删除结点在父结点的左还是右 if (cur == parent->_left) { parent->_left = cur->_left; } else { parent->_right = cur->_left; } } //删除结点并置空 delete cur; cur = nullptr; } //删除结点左右都不为空 //替换法删除(下面用右子树的最小结点写,两种都可) else { //min是右子树最小结点 //minparent是右子树最小结点父结点 Node* minparent = cur; Node* min = cur->_right; while (min->left) { minparent = min; min = min->_left; } //删除结点cur与右子树最小结点min交换 swap(cur->_key, min->_key); //判断min在minparent的左还是右 if (minparent->_left == min) { //避免min的还有右孩子 //这样的指向,不管有没有右孩子都对 minparent->_left = min->_right; } else { minparent->_right = min->_right; } delete min; } //删除完毕 return true; } } //二叉树全部找完,未找到待删结点 return false; } //中序遍历打印,以便观察 //中序的结果是升序 //写一个InOrder函数调用_InOrder函数 //可以调用到_root void InOrder() { _InOrder(_root); cout << endl; } /// //递归的写法 bool FindR(const K& key) { return _FindR(_root, key); } bool InsertR(const K& key) { return _InsertR(_root, key); } bool EraseR(const K& key) { return _EraseR(_root, key); } ~BSTree() { Destroy(_root); } //C++11用法:强制编译器生成默认的构造 //此时自己写了拷贝构造,编译器不会生成默认构造 BSTree() = default; BSTree(const BSTree & t) { //_root接收返回的copyroot _root = _Copy(t._root); } //赋值 t2 = t1 BSTree & operator=(BSTree t) { //t是t1的别名,而t1是我们所需要的 //因此交换_root和t._root后,满足需求 //并且出作用域交换后的t还会销毁,一举两得 swap(_root, t._root); return *this; } private: //配合拷贝构造 Node* _Copy(Node* root) { //如果传入的是空指针,则返回空指针 if (root == nullptr) { return nullptr; } //new一个copyroot,传入的root的key给它 Node* copyroot = new Node(root->_key); //前序遍历,先根,再左,在右 copyroot->_left = _Copy(root->_left); copyroot->_right = _Copy(root->_right); //遍历结束返回copyroot return copyroot; } //配合析构函数销毁 void Destroy(Node*& root) { if (root == nullptr) { return; } Destroy(root->_left); Destroy(root->_right); delete root; root = nullptr; } bool _FindR(Node* root, const K& key) { //递归到最后都没找到,返回false if (root == nullptr) return false; //如果找的值小于当前root值,递归左子树 if (root->_key > key) { return _FindR(root->_left, key); } //如果找的值大于当前root值,递归右子树 else if (root->_key < key) { return _FindR(root->_right, key); } //如果最终找到了,则返回true else { return true; } } //这里的Node*& root,表示根结点指针的引用 bool _InsertR(Node*& root, const K& key) { //Node*& root中的引用就用在这里 //当找到需要插入的地方root时是nullptr //引用可以保证不是局部变量,以免运行结束被销毁 //引用还可以保证这里的空指针是与它父结点连接着的 //因为这里是递归调用的,上面传的就是父结点的左或右 //将新结点插入后返回true,也就和父结点连接成功了 if (root == nullptr) { root = new Node(key); return true; } //如果找的值小于当前root值,递归左子树 if (root->_key > key) { return _InsertR(root->_left, key); } //如果找的值大于当前root值,递归右子树 else if (root->_key < key) { return _InsertR(root->_right, key); } //递归发现插入值出现过,返回false else { return false; } } //这里的Node*& root,和上面Insert的作用一样 bool _EraseR(Node*& root, const K& key) { //找删除的结点到最后没找到,则返回false if (root == nullptr) { return false; } //如果找的值小于当前root值,递归左子树 if (root->_key > key) { return _EraseR(root->_left, key); } //如果找的值大于当前root值,递归右子树 else if (root->_key < key) { return _EraseR(root->_right, key); } //找到待删除的结点,开始删除 else { //由于上面参数用了引用 //即root=它的父结点的左或右指针指向结点的别名 //所以若删除结点只有一个孩子的情况下 //先判断它的左右孩子哪个不为空 //然后给不为空的孩子链接起来 //root是删除结点的父结点的左或右指针的别名 //root->_right/_left是删除结点不为空的孩子 //将它的父结点链接到不为空的孩子结点上 //然后释放del就完成了删除 Node* del = root; if (root->_left == nullptr) { root = root->_right; } else if (root->_right == nullptr) { root = root->_left; } //两个孩子都不为空的情况 else { //找右子树的最左结点(最小)替换删除 Node* min = root->_right; while (min->_left) { min = min->_left; } //交换删除结点与右树最小结点的key swap(root->_key, min->_key); //递归,删除交换后的删除结点右树的结点 return _EraseR(root->_right, key); } delete del; return true; } } void _InOrder(Node* root) { if (root == nullptr) { return; } _InOrder(root->_left); cout << root->_key << " "; _InOrder(root->_right); } Node* _root = nullptr; }; 图片截图: