12.串，串的存储结构与模式匹配算法

目录

一. 一些术语

二. 串的类型定义

（1）串的顺序存储结构

（2）串的链式存储结构

三. 串的模式匹配算法

（1）BF算法

（2）KMP算法

四. 案例实现

---

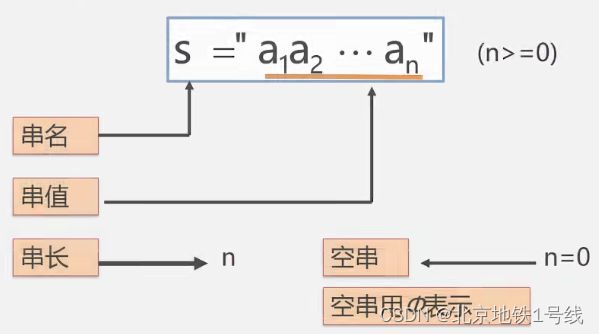
串(String)---零个或多个任意字符组成的有限序列。

一. 一些术语

子串：串中任意个连续字符组成的子序列称为该串的子串
主串：包含子串的串相应地称为主串
字符位置：字符在序列中的序号为该字符在串中的位置
子串位置：子串第一个字符在主串中的位置
空格串：由一个或多个空格组成的串，与空串不同

例如：给定字符串a、b、c、d，a='BEI'，b= 'JING'，c='BEIJING'，d='BEI JING'

它们的长度是： 3，4，7，8；
c的子串是：a，b；
d的子串是：a，b；
a在c中的位置是：1；a在d中的位置是：1；
b在c中的位置是：4；a在d中的位置是：5；

串相等：当且仅当两个串的长度相等并且各个对应位置上的字符都相同时，这两个串才是相等的。

二. 串的类型定义

串的抽象数据类型定义：同线性表，只不过处理对象是字符。

ADT String{
    数据对象:D={ ai | ai ∈ElemSet, i=1,2..,n, n≥0 }
    数据关系:R1= { | ai-1, ai∈D, i=2,...,n }
    基本操作:
    StrAssign (&T,chars)  //串赋值
    StrCompare (S,T)  //串比较
    StrLength (S)  //求串长
    Concat(&T,S1,S2)  //串连结
    Index(S,T,pos)  //求子串的位置
    ...还有其他操作...
}ADT String

与前面完全相同，串也可分为顺序串和链串。

（1）串的顺序存储结构

#define MAXLEN 255
typedef struct{
    char ch[MAXLEN+1];  //存储串的一维数组
    int length;  //串的当前长度
}SString;

说明：实际存储时通常是char ch[MAXLEN+1]，然后把第一个位置空出，这在处理一些问题时会简便一些。

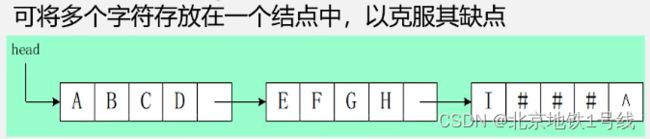
（2）串的链式存储结构

和链表不同的是，我们可以在一个结点有多个数据元素，这种结点我们称之为块，可以显著提高存储密度。

# define CHUNKSIZE 80  //块的大小可自定义
typedef struct Chunk{
    char ch[CHUNKSIZE];
    struct Chunk *next;
}Chunk;  //定义一个块的结点

typedef struct{
    Chunk *head,*tail;  //串的头指针和尾指针
    int curlen;  //串的当前长度
}LString;  //字符串的块链结构

三. 串的模式匹配算法

模式匹配算法的目的：确定主串中所含子串(模式串)第一次出现的位置 (定位)。针对模式匹配问题，我们有BF算法(Brute-Force, 又称古典的、经典的、朴素的、穷举的)和KMP算法（速度快），下面介绍这两种算法。

（1）BF算法

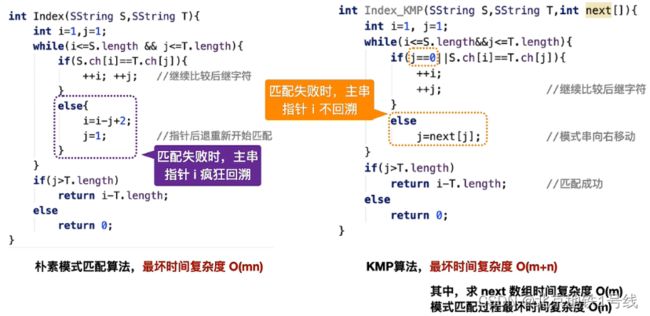
BF算法采用的基本思想是穷举法。将主串的第pos个字符和模式串的第一个字符比较。若相等，继续逐个比较后续字符；若不等，从主串S的下一字符起，重新与模式串T的第一个字符比较。例如，目标串的长度m=6，模式串的长度n=4。则先将目标串的1-4位与模式串对应1-4位逐个比较（i=1,j=1），然后起始位置加1，将目标串的2-5位与模式串对应1-4位逐个比较（i=2,j=1），最后将目标串的3-6位与模式串对应位逐个比较（i=3,j=1）。如果这时候还没有找到，则返回0，表示目标串中不存在对应的模式串。

这里还需要牵扯到一个回溯的问题：模式串T比较到第j位时发现匹配不成功，这个时候要进入下一轮匹配。模式串T中j直接置1（前面讲了，字符串第一个索引为0的位置空出来），那么目标串S中i应该置多少呢？上一轮匹配中模式串T从1到j位，往后挪了j-1步，所以目标串S中第一个被比较的字符所有是i-(j-1)，然后现在我们要进入下一轮循环，从这个字符的下一个字符开始，因此回溯的位置应该是i-(j-1)+1=i-j+2。

当匹配成功时，模式串T中指针j指向的位置索引应该是1+T.length，最后一个元素的下一个元素为空，退出循环，在此之前所有字符都匹配成功。所以返回的索引值应该是此刻的i值减去模式串的长度i-T.length。

下面给出BE算法的代码描述：

int Index_BF(SString S, SString T, int pos){
    int i=pos, j=1;  //从主串第pos位开始查找
    while (i<=S.length && j<=T.length) {
        if (S.ch[i]==T.ch[j]) {++i; ++j;}  //本字符对应位置匹配成功，主串和子串依次匹配下一个字符
        else {i=i-j+2;j=1;}  //本字符匹配不成功，主串、子串指针回溯重新开始下一次匹配
    }
    if (j>=T.length) return i-T.length; //这个时候在主串中找到了子串，返回匹配的第一个字符的下标 
    else return 0;  //直到所有循环结束仍没有在主串中找到子串，模式匹配不成功
}

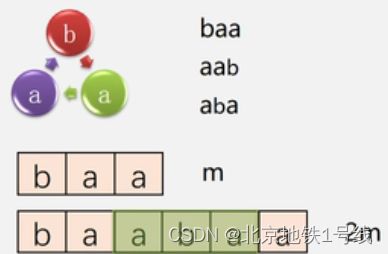
最后讨论算法的时间复杂度，如果主串S，子串T的长度为m,n，最多需要进行的循环次数是（m-n+1）次，每次比较n次，则最坏情况下的时间复杂度是O(（m-n+1）*n）。若n<

（2）KMP算法

此部分难度较大，建议看王道的视频动画演示，这里总结一下怎么求next数组和nextval数组：

4.2_2_KMP算法_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1b7411N798?p=36&vd_source=7bf292964a807d18168b0c665fed431cnext数组的求法（手算练习）：

• next[1]都无脑写0，next[2]都无脑写1；
• 其他next：在不匹配的位置前，划一根美丽的分界线，模式串一步一步往后退，直到分界线之前“能对上”，或模式串完全跨过分界线为止。此时j指向哪儿，next数组值就是多少。

例如，对于字符串google：

	g	o	o	g	l	e
next[0]	next[1]	next[2]	next[3]	next[4]	next[5]	next[6]
	0	1	1	1	2	1

KMP算法实际上就是改变了指针的回溯位置，主串中指针不回溯，子串中指针回溯的位置由next数组确定。next数组的作用就是：当子串的第j个字符失配时，从子串的第next[i]的继续往后匹配，而不一定非要从1开始。

nextval数组求解：

在此基础上进一步优化next数组，具体操作是，首先解出next数组，然后用以下步骤优化：

nextval [1]=0;
for (int j=2; j<=T.length; j++) {
    if (T.ch[next [j]]==T.ch[j])
        nextval[j]=nextval[next[j]];
    else
        nextval[j]=next[j];
}

例如，对以下字符串：

	a	b	a	b	b	a
next[0]	next[1]	next[2]	next[3]	next[4]	next[5]	next[6]
next数组	0	1	1	2	3	4
nextval数组	0	1	0	1	0	4

四. 案例实现

对于病毒检测：患病时，患者的DNA中包含病毒的DNA。但是病毒的DNA是环状的，也就是说假如aab是病毒的DNA，则aba，baa都是病毒的DNA。如图：

算法的主要思想如下：

• 对于每一个待检测的任务，假设病毒DNA序列的长度是m，因为病毒DNA序列是环状的，为了线性取到每个可行的长度为m的模式串，可将存储病毒DNA序列的字符串长度扩大为2m，将病毒DNA序列连续存储两次。
• 然后循环m次，依次取得每个长度为m的环状字符串，将此字符串作为模式串，将人的DNA序列作为主串，调用BF算法进行模式匹配。
• 只要匹配成功，即可中止循环，表明该人感染了对应的病毒;否则，循环m次结束循环时，可通过BF算法的返回值判断该人是否感染了对应的病毒。