机器学习西瓜书——基尼指数

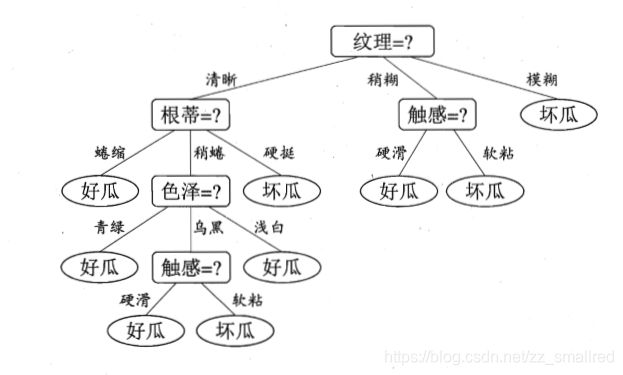
CART决策树使用“基尼指数”（Gini index）来选择划分属性。书上并没有写出具体的例子供参考，这里给出一个例子。

首先先列出求取基尼指数所需要用的公式。

数据集D的纯度可用基尼值来度量。Gini(D)越小，则数据集D的纯度越高。（Pk指的是正例在总体中的比例）

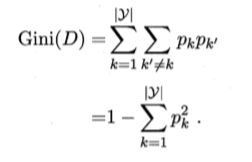
属性a的基尼指数定义为：

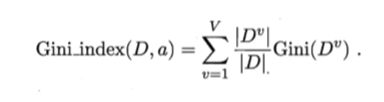
求取得出属性a的基尼指数后，再求取其他属性的基尼指数，最后比较获得基尼指数最小的属性为最优划分属性，并继续求取次级最优划分属性，以此类推，直到排序完成。

本例子运用的数据是书上给出的西瓜数据集2.0

这是色泽属性的图示。

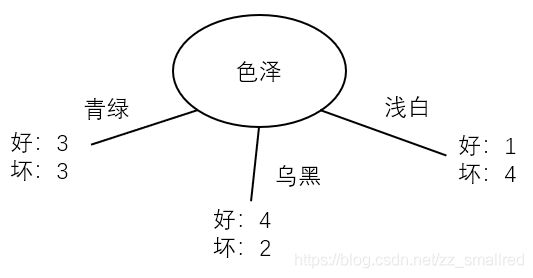
根据图示写出程序。

# 求取基尼值
def gini_index_single(a,b):
    single_gini = 1 - ((a/(a+b))**2) - ((b/(a+b))**2)
    return round(single_gini,4)

# 求取基尼指数
def gini_index(a,b,c,d,e,f):
    zuo = gini_index_single(a,b)
    zhong = gini_index_single(c,d)
    you = gini_index_single(e,f)
    sum = a+b+c+d+e+f
    gini_index = zuo*((a+b)/sum) + zhong*((c+d)/sum) + you*((e+f)/sum)
    return round(gini_index,4)

def gini_index2(a,b,c,d):
    zuo = gini_index_single(a,b)
    you = gini_index_single(c,d)
    sum = a+b+c+d
    gini_index2 = zuo*((a+b)/sum) + you*((c+d)/sum)
    return round(gini_index2,4)

依次求取色泽、根蒂、敲声、纹理、脐部、触感的基尼指数。如：

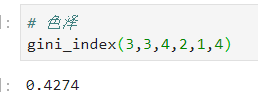
通过比较得出，纹理属性的基尼指数最小，为0.3046，为当前的最优划分属性。第一次分叉结束，接下来进行第二次分叉。（此时“纹理”属性不再作为候选划分属性。）

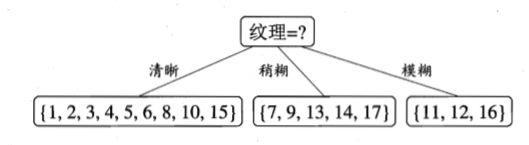
以图中第一个分支节点（纹理=“清晰”）为例，计算其他属性的基尼指数。
首先先计算该节点的纯度。（即基尼值）

def gini_index_single(a,b):
    single_gini = 1 - ((a/(a+b))**2) - ((b/(a+b))**2)
    return round(single_gini,4)
gini_index_single(7,2)

0.3457

此时再计算其他属性的基尼指数，纹理清晰的色泽、根蒂、敲声、脐部、触感的基尼指数分别为0.3333、0.1481、0.1852、0.1481、0.1481。“根蒂”、“脐部”、“触感”三个属性的基尼指数相等，且都比该节点的数值要小（0.3457<0.1481），所以该节点应当继续进行分叉。

此时我们选择使用属性“根蒂”继续进行分叉。当我们使用“蜷缩”属性进行计算时，由于该样本中纹理清晰且根蒂蜷缩的西瓜都是好瓜，所以该节点无法继续进行分叉。（即该节点基尼值为0，没有更小的基尼值了）

def gini_index_single(a,b):
    single_gini = 1 - ((a/(a+b))**2) - ((b/(a+b))**2)
    return round(single_gini,4)
gini_index_single(5,0)

0.0

我们换用另外一个节点“稍蜷”，发现可以继续进行分叉，继续分叉。

经过计算，最后得到的决策树如下：